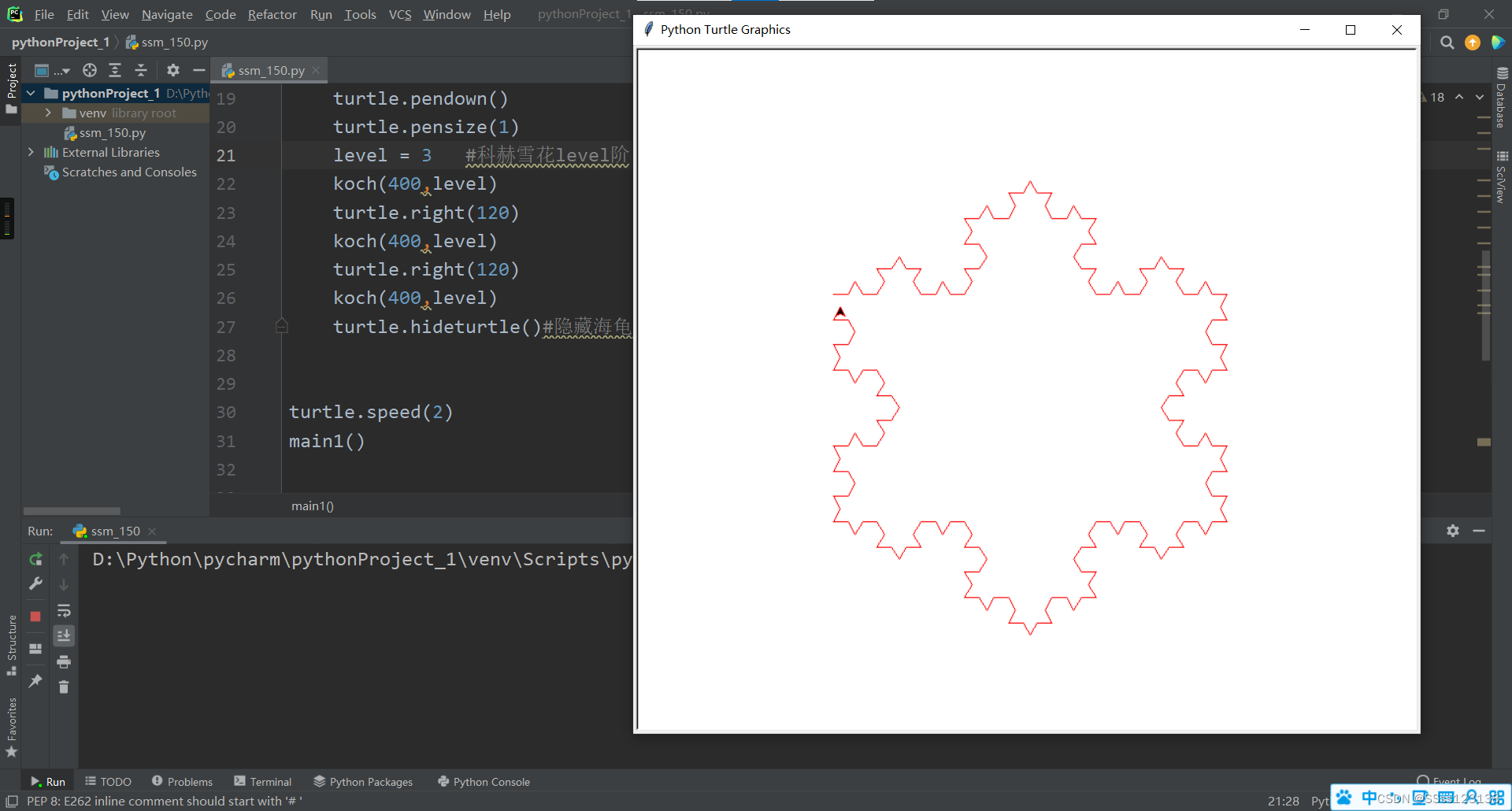
提要:基于MOOC的“Python语言程序设计基础”,主讲人:嵩天。基本算是课本笔记。
科赫雪花曲线设计思路
一、三种人类思维特征
逻辑思维:推理和演绎,数学为代表;
实证思维:实验和验证,物理为代表;
计算思维:设计和构造,计算机为代表;
二、计算思维的概念
概念诞生:2006年,时任美国卡内基-梅隆大学计算机系主任的周以真(Jeannette M. Wing)教授,提出了计算思维(Computational Thinking)概念——第一次从思维层面阐述了运用计算机科学的基础概念,来求解问题、设计系统和理解人类行为的过程。
实践手段:程序设计,是实践计算思维的重要手段。
解决思路:抽象实际问题的计算特性、利用计算机求解。
本质:抽象化(abstraction)和自动化(Automation)。
三、实例运用计算思维
在程序设计范涛,计算思维主要反映在如下几个方面:理解问题的计算特性、将计算特性抽象为计算问题、通过程序设计语言实现问题的自动求解等。
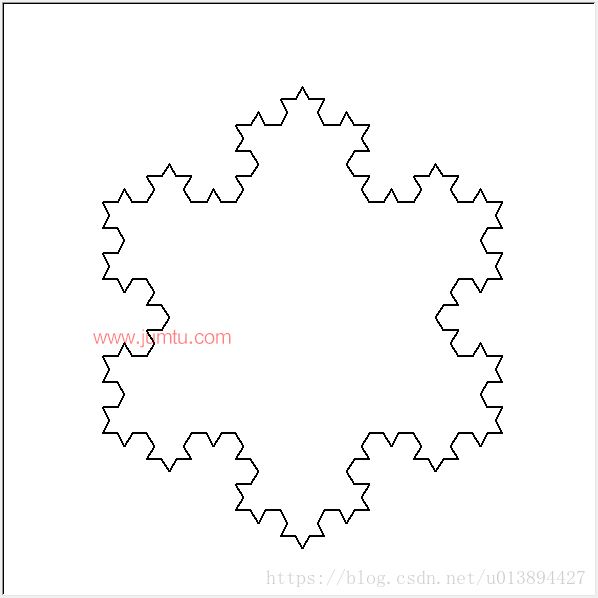
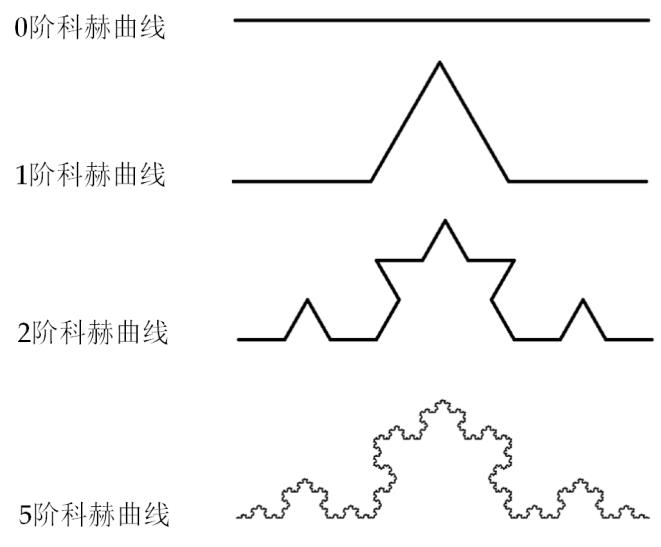
实例:科赫雪花曲线
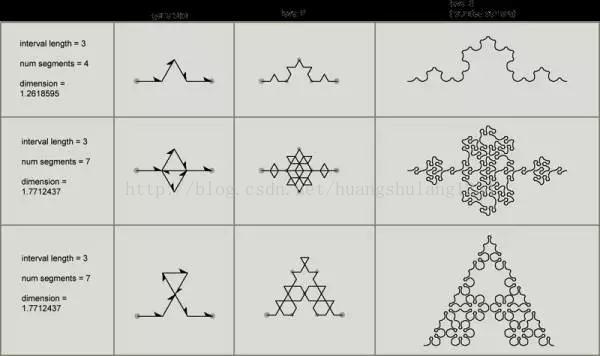
看图:(分别是0阶、1阶、2阶和3阶科赫雪花曲线)
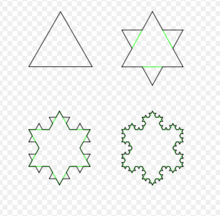
科赫雪花曲线总体思路:
分析科赫雪花曲线,发现可分解为基本&可重复的单元;
将这些单元设计为程序设计语言;
最后,通过计算机自动求解。
1st:理解问题的计算特性
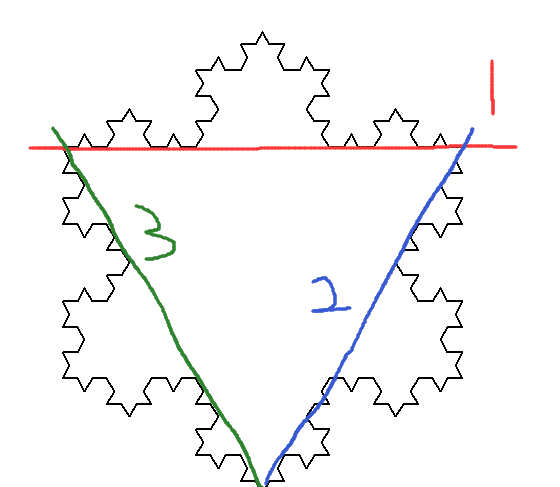
通过分析,科赫雪花曲线的“基本&可重复“单元为两个层次:
- 从0阶科赫雪花曲线看出,可将三条边分解为一个基本单元——不妨叫它“边”,的3次重复性问题;
- 从大于0阶的科赫雪花曲线可以看出,可将每个边分为4个基本单元——不妨叫它“尖”,的4次重复性问题;
2nd:将计算特性抽象为计算问题
首先,定计算问题的对象:要计算的问题是“边”和“尖”,
其次,定计算问题的顺序:由“尖”组成“边”,再由“边”组成我们需要的“科赫雪花曲线”,
最后,定计算问题的参数:见第三步。
3rd:将计算问题转化为成设计语言
首先,定需要的工具(程序包):我们选择turtle,
其次,定需要设定的程序框架:我们选择“函数”,利用其“复用”和“递归”的特性,实现计算的”基本&可重复性“单元,
最后,定程序需要的接口参数:一个是科赫雪花曲线的“阶数”,另一个是科赫雪花曲线的“长度”后者称作“大小”。
四、解决方法
整体代码如下:
import turtle # 引入决解问题需要的工具——turtle作图包
# 定义turtle画笔和画布的参数
def huabi():
turtle.speed(0) # speed()参数有[0,10]:“0”特殊、代表最快速度,其余[1,10]值越大、速度越快
turtle.pensize(2) # 设置画笔宽度为2
turtle.setup(800,800, 100, 10) # setup()参数有4个:前两个代表画布的“宽”和“高”,当数值为整数时、表示绝对像素大小,当小数时、表示站屏幕的比例。后两个可以省略,默认为屏幕中心位置,代表距离“屏幕左上角”的距离,单位是像素密度,
turtle.penup() # 抬起画笔,之后的画笔动作、就不会产生图线
turtle.goto(-300, 100) # 以画布中心点为坐标原点(0,0),将画笔移动到坐标(-300,100)处
turtle.pendown() # 落下画笔,以便画图
# 定义“尖”
def koch(size, n):
if n==0: # 0阶的科赫雪花曲线就是一条线,大小为输入的“size”
turtle.fd(size)
else: # 高阶科赫雪花曲线
for i in [0, 60, -120, 60]: # turtle在“尖”的四条线上改变的角度,分别为0°,60°,-129°,60°
turtle.left(i) # 对应上边四个角度,一共需要转4次弯,画出本阶的四条线,
koch(size/3, n-1) # 每个角度下的一个边,对应低一阶的客户雪花曲线的“尖”;至此完成函数本身的循环和复用,自动画出一个完整的n阶“尖”
# 定义“边”
def sdkoch(size, n): # 完整的科赫雪花曲线由3个“边”组成,我们以上完成的是一个由“尖”组成的“边”,
koch(size, n)
turtle.right(120) # 2行代码一组,
koch(size, n)
turtle.right(120)
koch(size, n) # 至此,得到完整的n阶科赫雪花曲线
turtle.hideturtle() # 把turtle的光标隐藏
turtle.done() # 结束turtle
# 定义main()主函数
def main(size, n): # 设定参数接口
huabi()
sdkoch(size, n)
main(500, 2) # 在设定参数之后,调用主函数
附注:自己的思路
对于我,最难的时函数循环和复用部分:一开始把最基本的科赫雪花曲线组分、设为了1阶;但是,在推广到n阶时遇到问题,才不得不把基本组分设为0阶。
当初的错误胆码及思路:
第一步:写出最基本组分:1阶“尖”
if n == 1:
for i in [0, 60, -120, 60]:
turtle.left(i)
turtle.fd(size/3)
第二部:将基本组分推广到高阶,途径是利用高一阶——2阶,的组分
def koch(size, n):
if n == 1:
for i in [0, 60, -120, 60]: # for in()函数,即遍历取值函数,使得i分别取0,60,-120和60,分别带入for in()循环后边的程序
turtle.left(i)
turtle.fd(size/3)
else:
koch(size/3, n-1)
显然,结果错误。因为每个高阶科赫雪花曲线“尖”的4个线段,每一个线段都是由低一阶科赫雪花曲线的“尖”组成,意味着
koch(size/3, n-1)必须在 for in ()循环下。据此修改如下:
def koch(size, n):
if n==1:
for i in [0, 60, -120, 60]:
turtle.left(i)
turtle.fd(size/3)
else:
for i in [0, 60, -120, 60]: # for in()函数,即遍历取值函数,使得i分别取0,60,-120和60,分别带入for in()循环后边的程序
turtle.left(i)
koch(size/3, n-1)
但时明显没有如下简单:(我想,最关键的时没有把0阶,即三角形,视为科赫雪花曲线的缘故):
def koch(size, n):
if n==0:
turtle.fd(size)
else:
for i in [0, 60, -120, 60]:
turtle.left(i)
koch(size/3, n-1)