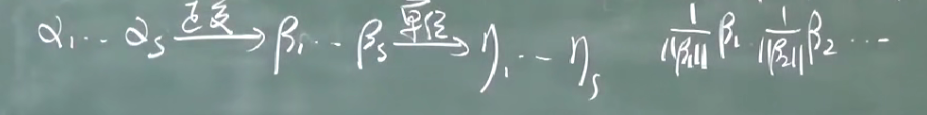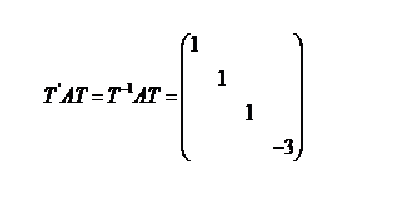1 前端架构介绍
1.1前端核心技术

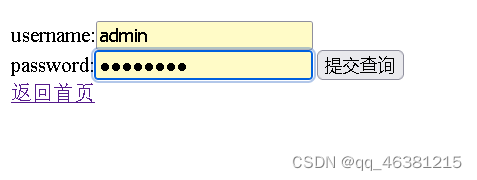
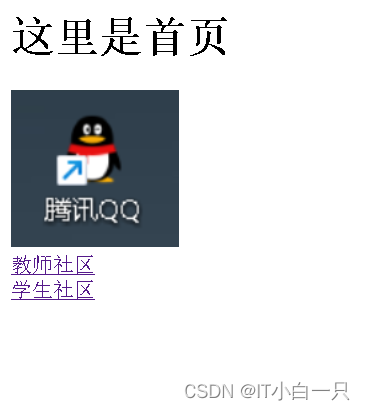
主要是讲解了web的前端框架,讲了网页文件的各个作用,然后进行了演示,演示了网页html的书写与跳转,包括创建表单,登录,页面跳转。然后进行了实操。
实训日志day3
article/2025/9/22 13:13:10
相关文章
Java实训日志06
文章目录 八、项目开发实现步骤(八)创建服务接口1、创建学校服务接口2、创建状态服务接口3、创建学生服务接口4、创建用户服务接口 (九)创建服务接口实现类1、创建学校服务接口实现类2、创建状态服务接口实现类3、创建学生服务接口…
实习日志03-技术02
本节:工作中经常会从别的项目复制一样的功能来使用。以下,是在此过程中,一不小心就会踩到的坑。
1.前端写好了,但是调取接口有问题,还有可能是没有更新后端的代码,更新一下代码及就可以了。
2.复制代码&a…
JAVAEE 实训日志 一
文章目录 1. 创建 web-app 项目导入初始4个 maven 依赖TestServlet.javatest.jsp测试: 2. 连接数据库导入依赖 驱动编写连接类 JDBCUtil测试连接 3. 开发一个简单的javaweb项目EntityService 层DaoController前端 test.jsp效果 1. 创建 web-app 项目
导入初始4个 maven 依赖 &…
Java实训日志04
文章目录 八、项目开发实现步骤(六)创建数据访问接口1、创建学校数据访问接口2、创建状态数据访问接口3、创建学生数据访问接口4、创建用户数据访问接口 八、项目开发实现步骤
(六)创建数据访问接口
DAO: Data Acess Object - 数…
项目实训-个人开发日志02-初识微信小程序开发
今天开始正式进入微信小程序端的开发,由于本人从未学习过小程序开发,所以在此一并把学习过程记录。 安装微信开发者工具,以非云开发的基础模板创建文件,得到如下项目结构: page即为页面,目前有两个文件夹&…
JAVA实训项目第六次日志
实训目的:让学生综合运用J2SE有关知识开发【学生信息管理系统】。主要涉及程序控制结构、面向对象编程、图形用户界面、Java数据库应用、MySQL数据库这几个方面的内容。通过本项目的开发,让学生了解系统开发的一般流程,初步了解MVC模式与单元…
实对称矩阵可对角化证明
在极化分解的证明中使用过此定理,证明于此。 埃尔米特矩阵是指复对称矩阵,实对称矩阵是其特例。 转载于:https://www.cnblogs.com/zhixingr/p/8750210.html
线性代数笔记5.3实对称矩阵的对角化(前瞻知识)
实对称矩阵都能对角化
内积
简单来说,内积就是两个向量的对应分量相乘再相加
内积是个数!!
内积的性质
注意最后一条性质
两个向量和与第三个向量的内积 两个向量分别与第三个向量内积的和,这条性质可以与上面的性质配合使…
含重根的三阶实对称矩阵的快速对角化方法
众所周知,实对称矩阵一定可以相似对角化。而考试中考察的三阶实对称矩阵对角化基本都是三阶的。而且正常情况下特征根一定是整数。因此基于此,有一些特殊的方法可以快速计算三阶实对称矩阵的特征值和特征向量。 一. 猜根法计算特征值 特征值之和等于矩阵…
实对称矩阵必可正交对角化证明
我的小程序: 待办计划:给自己立个小目标吧! n阶矩阵A可正交对角化的充分条件是A是实对称矩阵,即若A是实对称矩阵则A必可正交对角化。
首先,有以下定理:
若的特征值为,且,则存在正交…