点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
转载| 机器人配视觉
今天介绍一下深度图像的获取方法主要有哪些,以及这些方法会导致深度图像中存在什么样的问题。
在计算机视觉系统中,三维场景信息为图像分割、目标检测、物体跟踪等各类计算机视觉应用提供了更多的可能性,而深度图像(Depth map)作为一种普遍的三维场景信息表达方式得到了广泛的应用。深度图像的每个像素点的灰度值可用于表征场景中某一点距离摄像机的远近。
获取深度图像的方法可以分为两类:被动测距传感和主动深度传感。
In short:深度图像的像素值反映场景中物体到相机的距离,获取深度图像的方法=被动测距传感+主动深度传感。
被动测距传感
被动测距传感中最常用的方法是双目立体视觉[1,2],该方法通过两个相隔一定距离的摄像机同时获取同一场景的两幅图像,通过立体匹配算法找到两幅图像中对应的像素点,随后根据三角原理计算出时差信息,而视差信息通过转换可用于表征场景中物体的深度信息。基于立体匹配算法,还可通过拍摄同一场景下不同角度的一组图像来获得该场景的深度图像。除此之外,场景深度信息还可以通过对图像的光度特征[3]、明暗特征[4]等特征进行分析间接估算得到。
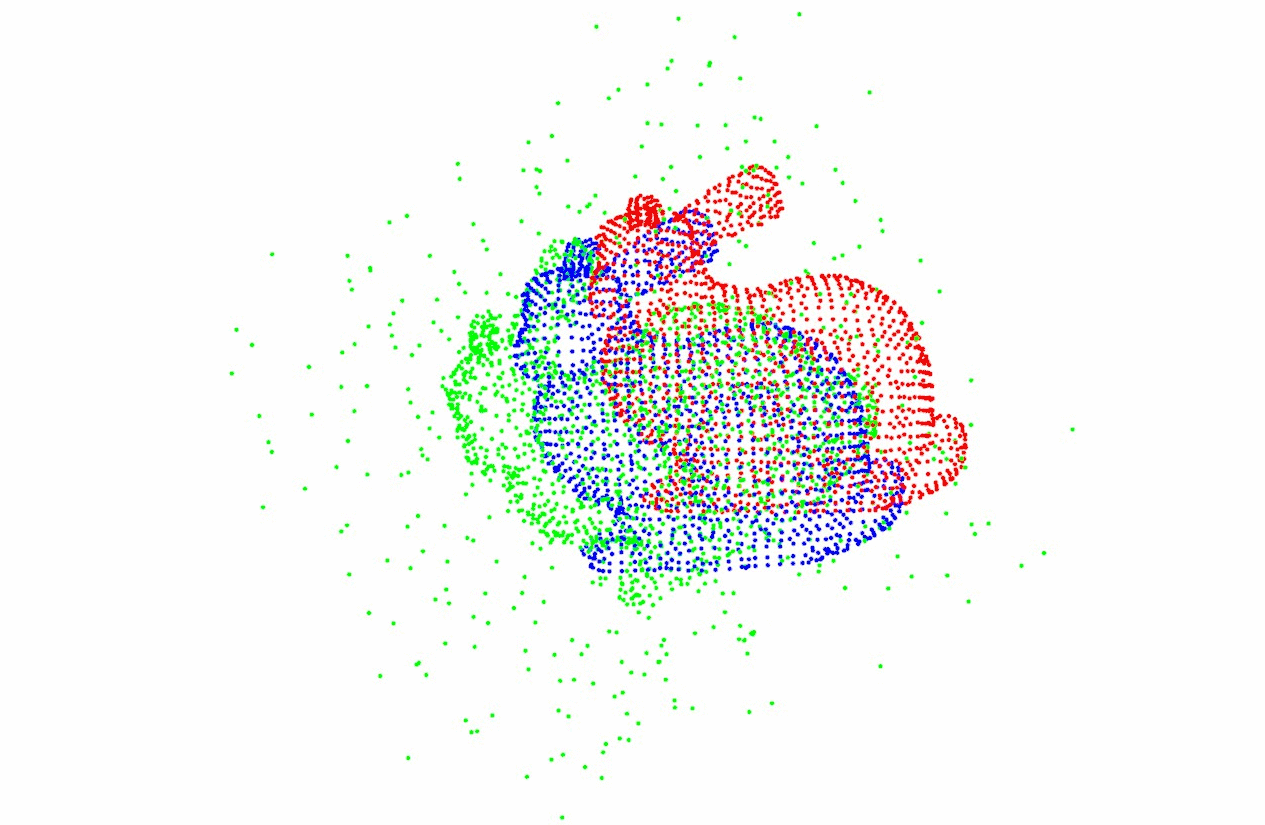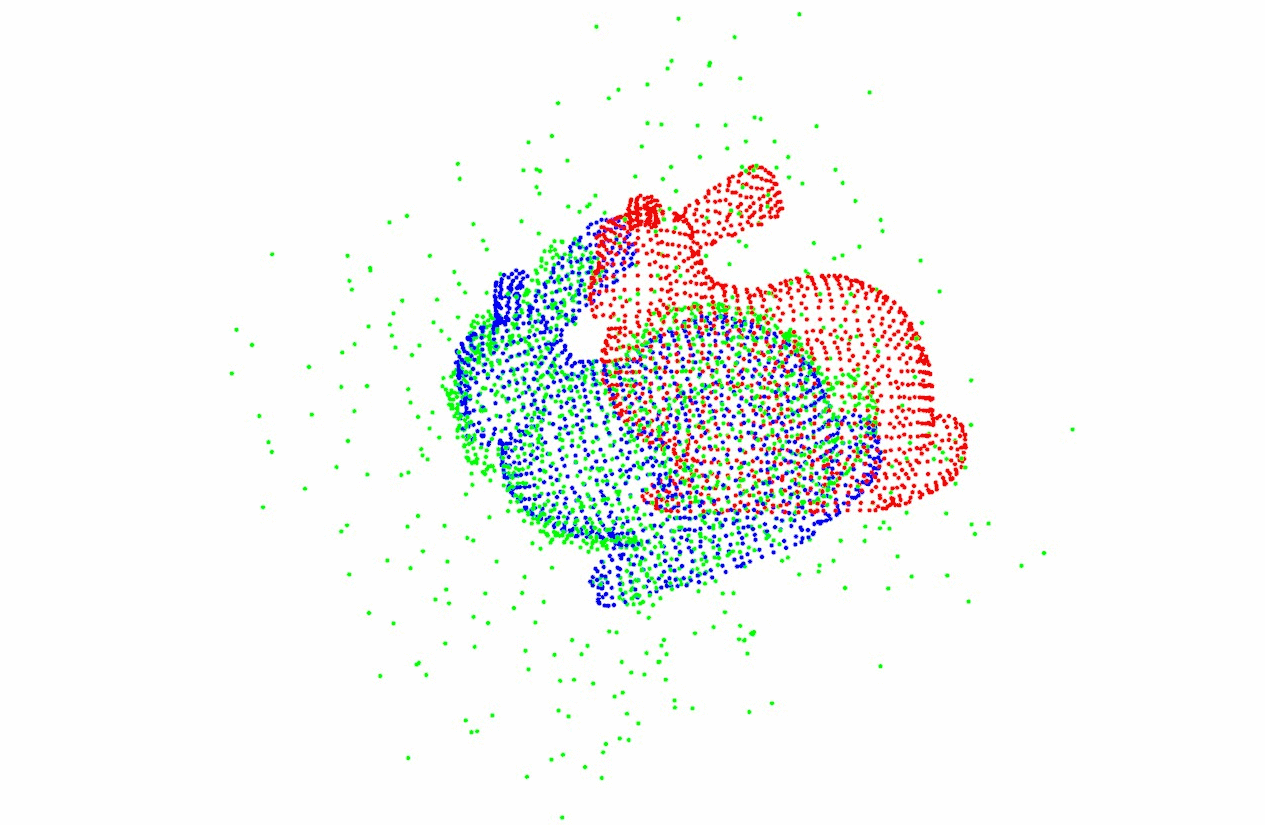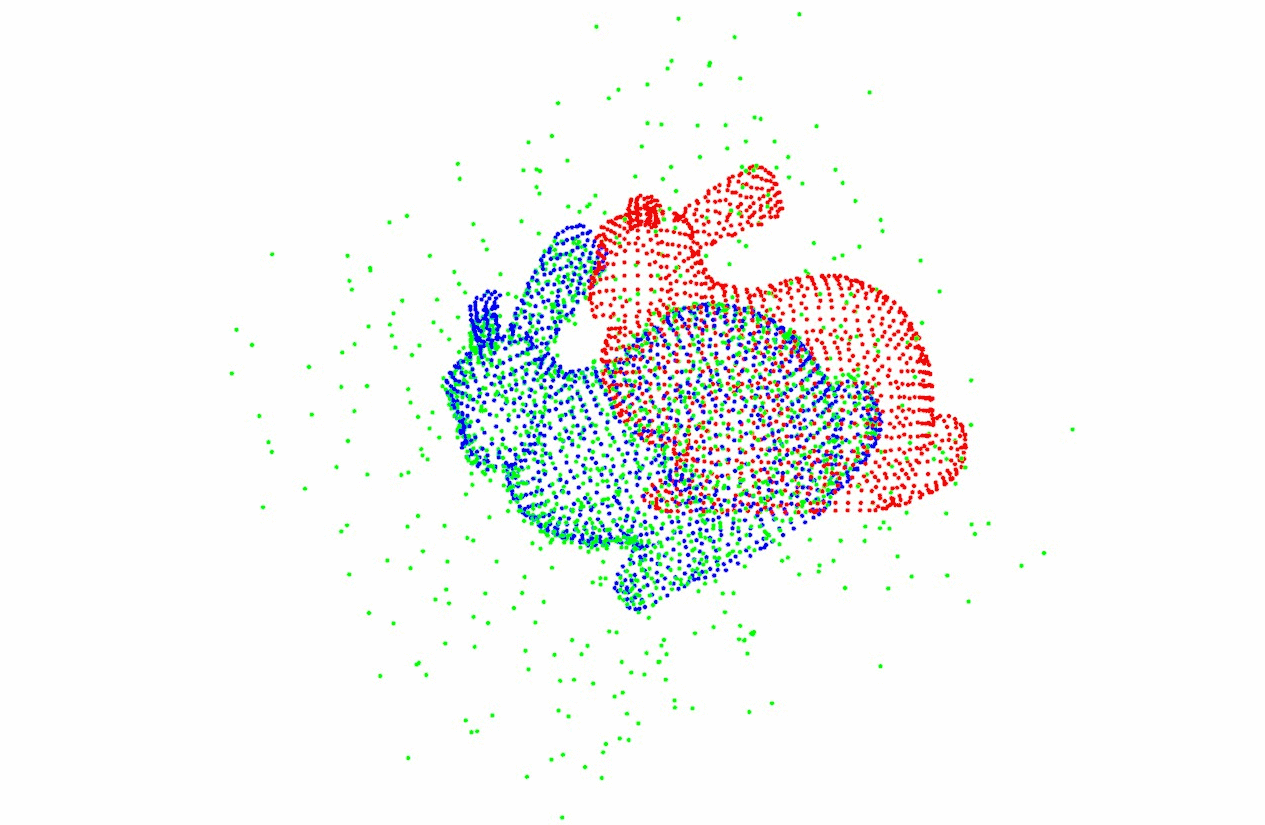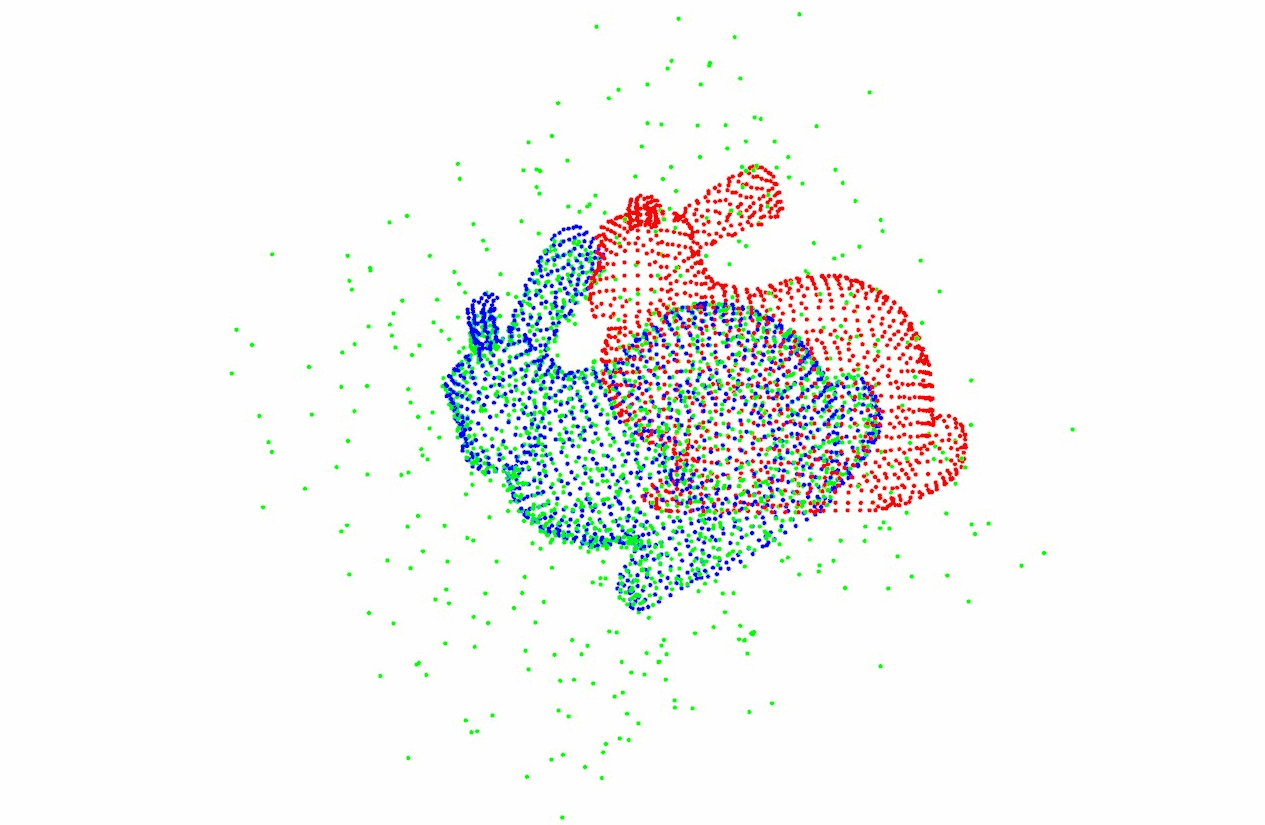
上图展示了Middlebury Stereo Dataset中Tsukuba场景的彩色图像、视差实际值与用Graph cuts算法得到的立体匹配误差估计结果,该视差图像可以用于表征场景中物体的三维信息。
可以看到,通过立体匹配算法得到的视差图虽然可以得到场景的大致三维信息,但是部分像素点的时差存在较大误差。双目立体视觉获得视差图像的方法受限于基线长度以及左右图像间像素点的匹配精确度,其所获得的视差图像的范围与精度存在一定的限制。
In short, 常用于深度图像增强领域的测试数据集Middlebury Stereo Dataset属于被动测距传感;被动测距传感=两个相隔一定距离的相机获得两幅图像+立体匹配+三角原理计算视差(disparity)
主动测距传感
主动测距传感相比较于被动测距传感最明显的特征是:设备本身需要发射能量来完成深度信息的采集。这也就保证了深度图像的获取独立于彩色图像的获取。近年来,主动深度传感在市面上的应用愈加丰富。主动深度传感的方法主要包括了TOF(Time of Flight)、结构光、激光扫描等。
TOF相机
TOF相机获取深度图像的原理是:通过对目标场景发射连续的近红外脉冲,然后用传感器接收由物体反射回的光脉冲。通过比较发射光脉冲与经过物体反射的光脉冲的相位差,可以推算得到光脉冲之间的传输延迟进而得到物体相对于发射器的距离,最终得到一幅深度图像。
TOF相机所获得的深度图像有以下的缺陷:
1. 深度图像的分辨率远不及彩色图像的分辨率
2. 深度图像的深度值受到显著的噪声干扰
3. 深度图像在物体的边缘处的深度值易出现误差,而这通常是由于一个像素点所对应的场景涵盖了不同的物体表面所引起的。
除此之外,TOF相机的通常价格不菲。
结构光与Kinect
结构光是具有特定模式的光,其具有例如点、线、面等模式图案。
基于结构光的深度图像获取原理是:将结构光投射至场景,并由图像传感器捕获相应的带有结构光的图案。
由于结构光的模式图案会因为物体的形状发生变形,因此通过模式图像在捕捉得到的图像中的位置以及形变程度利用三角原理计算即可得到场景中各点的深度信息。
结构光测量技术提供了高精度并且快速的三维信息,其在汽车、游戏、医疗等领域均已经得到了广泛的应用。
基于结构光的思想,微软公司推出了一款低价优质的结合彩色图像与深度图像的体感设备Kinect,该设备被应用于如人机交互(Xbox系列游戏机)、三维场景重建、机器视觉等诸多领域。
微软公司的Kinect有三个镜头,除了获取RGB彩色图像的摄像机之外,左右两边的镜头分别是红外线发射器和红外线CMOS摄像机,这两个镜头共同构成了Kinect的深度传感装置,其投影和接收区域相互重叠,如下图所示。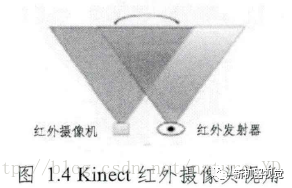
Kinect采用了一种名为光编码(Light Coding)的技术,不同于传统的结构光方法投射一幅二维模式图案的方法,Kinect的光编码的红外线发射机发射的是一个具有三维纵深的“立体编码”。光编码的光源被称为激光散斑,其形成原理是激光照射到粗糙物体或穿透毛玻璃后得到了随机的衍射斑点。激光散斑具有高度的三维空间随机性。当完成一次光源标定后,整个空间的散斑图案都被记录,因此,当物体放进该空间后,只需得知物体表面的散斑图案,就可以知道该物体所处的位置,进而获取该场景的深度图像。红外摄像机捕获的红外散斑图像如下图所示,其中左侧的图片展现了右侧图片中框中的细节。

Kinect低廉的价格与实时高分辨率的深度图像捕捉特性使得其在消费电子领域得到了迅猛发展,然而Kinect的有效测距范围仅为800毫米到4000毫米,对处在测距范围之外的物体,Kinect并不能保证准确深度值的获取。Kinect捕获的深度图像存在深度缺失的区域,其体现为深度值为零,该区域意味着Kinect无法获得该区域的深度值。而除此之外,其深度图像还存在着深度图像边缘与彩色图像边缘不对应、深度噪声等问题。Kinect所捕获的彩色图像与深度图像如下图所示。
Kinect所捕获的深度图像产生深度缺失区域的原因多种多样。除了受限于测距范围,一个重要的原因是目标空间中的一个物体遮挡了其背后区域。这种情况导致了红外发射器所投射的图案无法照射到背后区域上,而背后区域却有可能被处在另一个视角的红外摄像机捕捉到,然而该区域并不存在散斑图案,该区域的深度信息也就无法被获得。【Oops,原来遮挡是这样导致了深度值缺失,作者果然厉害,两句话让人茅塞顿开!】物体表面的材质同样会影响Kinect深度图像的获取。当材质为光滑的平面时,红外投射散斑光束在物体表面产生镜面反射,红外摄像机无法捕捉该物体反射的红外光,因此也就无法捕获到该表面的深度;当材质为吸光材料时,红外投射散斑被该表面所吸收而不存在反射光,红外摄像机同样无法捕捉到该表面的深度信息。【材质对深度缺失的影响,分析到位】除此之外,Kinect所捕获的深度图像存在的与彩色图像边缘不一致的问题主要是由彩色摄像机与红外摄像机的光学畸变引起的。
激光雷达
激光雷达测距技术通过激光扫描的方式得到场景的三维信息。其基本原理是按照一定时间间隔向空间发射激光,并记录各个扫描点的信号从激光雷达到被测场景中的物体,随后又经过物体反射回到激光雷达的相隔时间,据此推算出物体表面与激光雷达之间的距离。
激光雷达由于其测距范围广、测量精度高的特性被广泛地用于室外三维空间感知的人工智能系统中,例如自主车的避障导航、三维场景重建等应用中。下图展示的是激光雷达Velodyne HDL-64E在自主车中的应用,该激光雷达能够获取360°水平方向上的全景三维信息,其每秒能够输出超过130万个扫描点的数据。全向激光雷达曾在美国举办的DARPA挑战赛中被许多队伍所采用,其也成为了自主行驶车辆的标准配置。
然而,激光雷达所捕获的三维信息体现在彩色图像坐标系下是不均匀并且稀疏的。由于单位周期内,激光扫描的点数是有限的,当把激光雷达捕获的三维点投射到彩色图像坐标系下得到深度图像时,其深度图像的深度值以离散的点的形式呈现,深度图像中许多区域的深度值是未知的。这也就意味着彩色图像中的某些像素点并没有对应的深度信息。
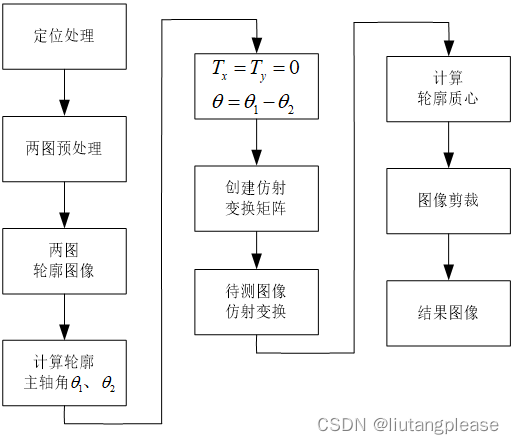
总结
用一个图来总结下内容吧。