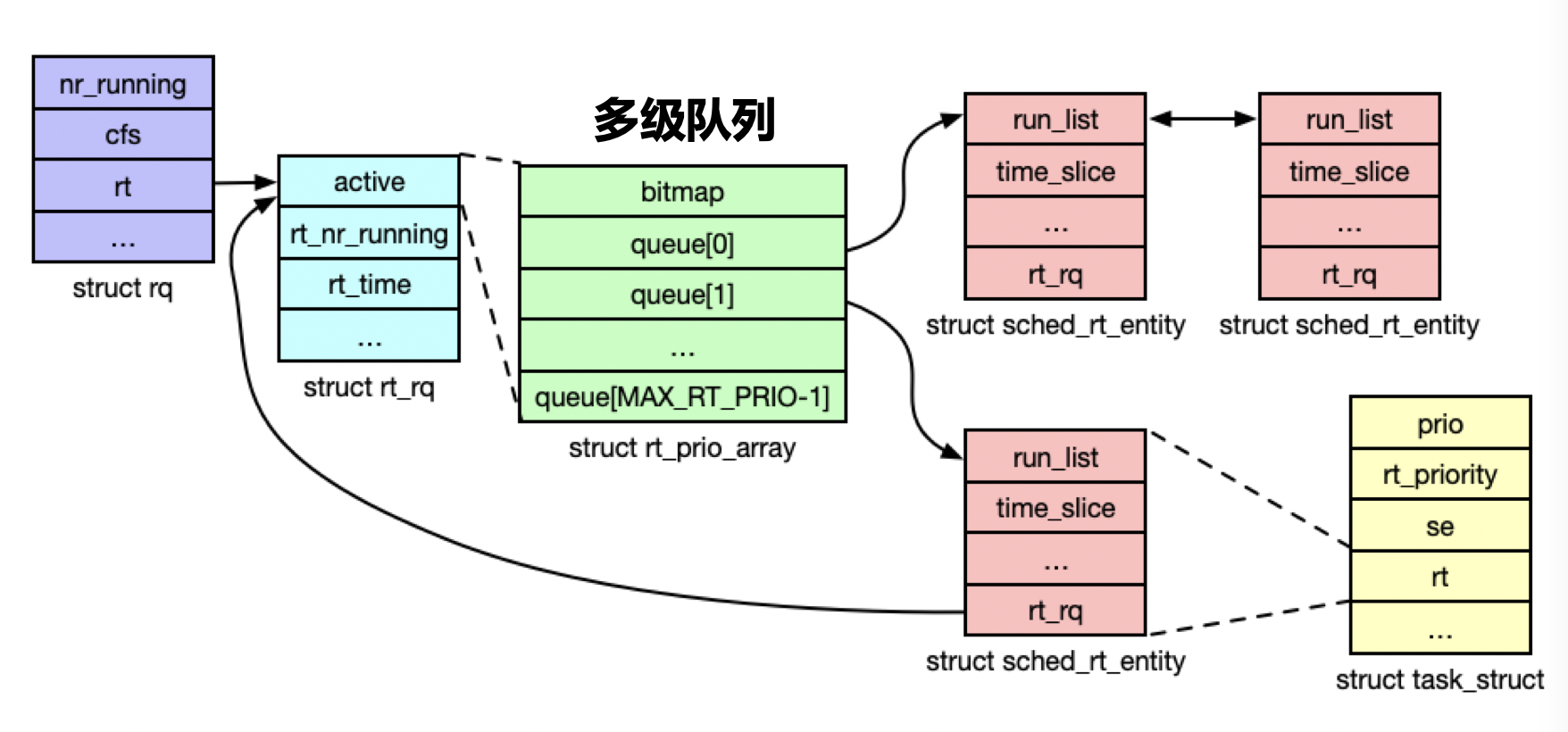
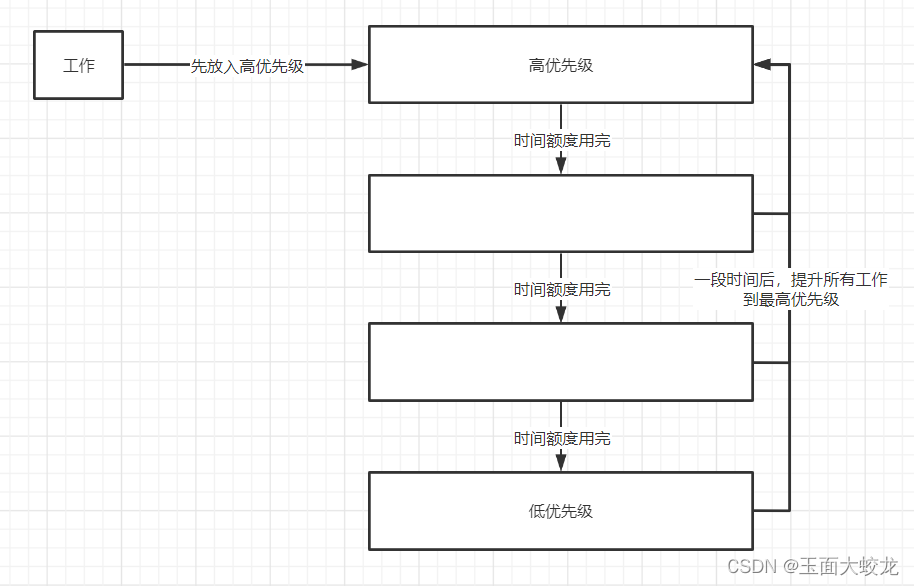
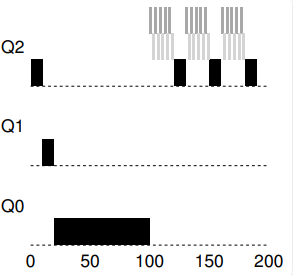
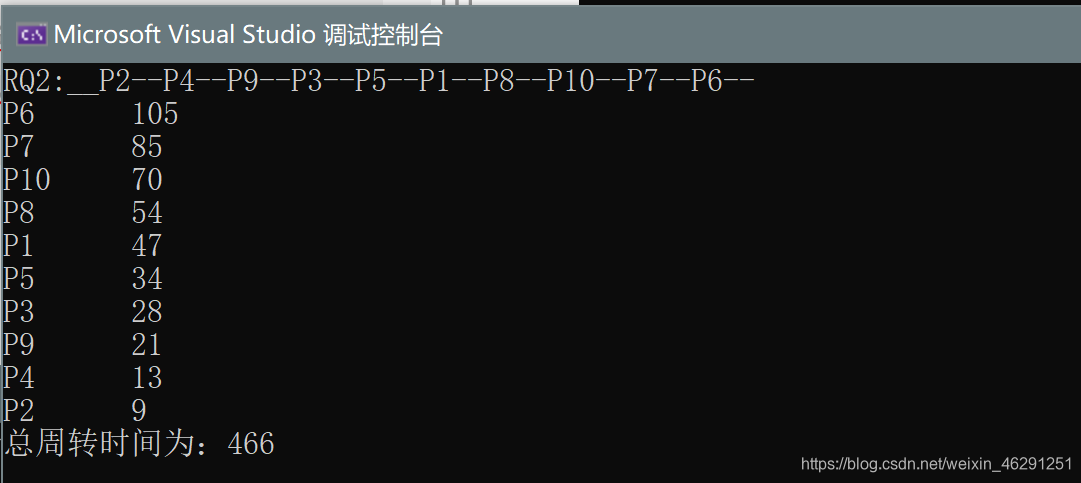
介绍

        前段时间比较忙，没有更新，这次的也是操作系统的一个实践作业 C++实现非抢占式多级反馈队列优先级调度算法，希望可以帮到你们。

问题介绍

这里我用课件里的内容

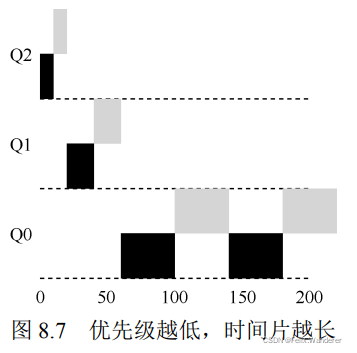
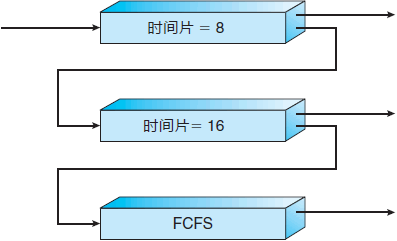
        1.应设置多个就绪队列，并为每个队列赋予不同的优先级。第一个队列的优先级最高，第二个队列次之，其余各队列的优先权逐个降低。该算法赋予各个队列中进程执行时间片的大小也各不相同，在优先权愈高的队列中，为每个进程所规定的执行时间片就愈小。

 

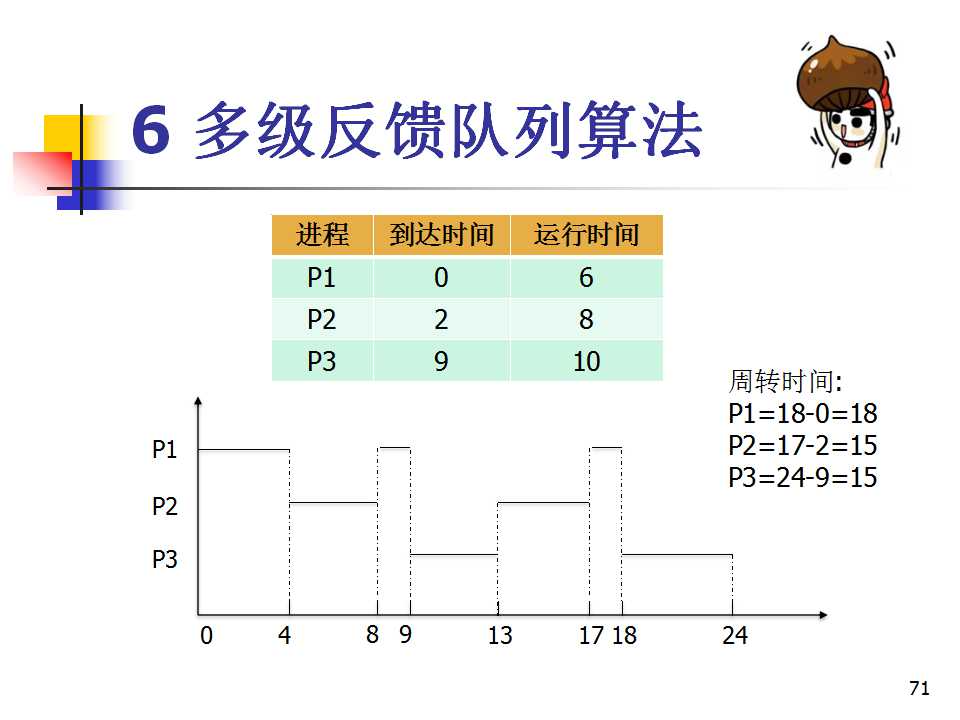
        2.新进程进入内存后，首先将其放在第一队列的末尾，按FCFS原则排队等待调度。当轮到该进程执行时，如它能在该时间片内完成，便可准备撤离系统；如果它在一个时间片结束时尚未完成，调度程序便将该进程转入第二队列的末尾，…如此下去，最后一个队列中采取时间片轮转的方式运行。

       3.仅当较高优先级的队列为空，才调度较低优先级的队列中的进程执行。

代码

        下面是我写的代码，由于时间仓促，如果在运行过程中有错误的地方，请在评论区私信我。

#include<iostream>
#include<string>
#include<queue>
#include<algorithm>
#include<iomanip>
using namespace std;
/* 分别定义三个队列时间片长度 */ 
#define firstCpu 1
#define secondCpu 2
#define thirdCpu 3class Process //定义进程类，包含进程名，到达时间，执行时间 
{public:Process();Process(string n, int time1, int time2,int time3); string name;int arrive_time;int Need_time;int need_time;int begin_time;int run_time;int end_time;bool first_run;
};Process::Process(string n, int time1, int time2,int time3)
{name = n;arrive_time = time1;need_time = time2;Need_time = time3;run_time =  -1;begin_time= -1;end_time = -1;first_run=0;
}Process::Process()
{name = "none";arrive_time= 200;need_time = -1; begin_time = 0;Need_time = 0;end_time = 0;run_time =0;first_run=0;
}Process process[100];
Process finish[100];
int c=0;
int num;
bool cmp(Process p1,Process p2)
{return p1.arrive_time<p2.arrive_time;
}void printP(Process &p)
{cout<<p.name<<"          "<<p.begin_time<<"          "<<p.end_time<<"          "<<p.run_time<<"          "<<setprecision(2)<<fixed<<double(p.end_time-p.arrive_time)/double(p.Need_time)<<endl;
}void Input() //输入函数 
{cout<<"请输入进程总数(小于100):";cin>>num;cout<<endl;string n;int time1;int time2;for(int i=0;i<num;i++){cout<<"请依次输入进程信息"<<endl;cout<<"请输入进程代号:";cin>>n;cout<<"请输入到达时间:";cin>>time1;cout<<"请输入服务时间:";cin>>time2;process[i]=Process(n,time1,time2,time2);	cout<<endl;} 
}void Running(queue<Process>line_1,queue<Process>line_2,queue<Process>line_3) //执行函数 
{int number = 0;int currentTime = 0; int firstTime = firstCpu;int secondTime = secondCpu;int thirdTime = thirdCpu;if(process[0].arrive_time>0){currentTime=process[0].arrive_time;}while(number<num||!line_1.empty()||!line_2.empty()||!line_3.empty()) //结束条件队列为空而且所有进程都加入队列 {while(number<num&&process[number].arrive_time==currentTime) //莫一时刻进程到来，加入第一队列 {line_1.push(process[number++]);
//			printP(line_1.back());}if(!line_1.empty())        //在第一个队列执行 {if(line_1.front().first_run==0){line_1.front().first_run=1;line_1.front().begin_time=currentTime;}line_1.front().need_time-=1;firstTime--;currentTime++;if(line_1.front().need_time>0){if(firstTime==0){   line_2.push(line_1.front());line_1.pop();firstTime = firstCpu;}}	else if(line_1.front().need_time==0){
//				cout<<"当前时刻："<<currentTime<<"进程结束:"<<endl;line_1.front().run_time=currentTime - line_1.front().begin_time;line_1.front().end_time=currentTime;finish[c]=line_1.front();
//				printP(line_1.front());c++;line_1.pop();firstTime = firstCpu;}}else if(!line_2.empty())  //第一队列为空，第二队列不为空 {while(secondTime>0){line_2.front().need_time--;secondTime--;currentTime++;while(number<num&&process[number].arrive_time==currentTime){line_1.push(process[number++]);}if(line_2.front().need_time==0)break;}	if(line_2.front().need_time>0){line_3.push(line_2.front());line_2.pop();secondTime = secondCpu;}	else if(line_2.front().need_time==0){line_2.front().run_time=currentTime - line_2.front().begin_time;line_2.front().end_time=currentTime;finish[c]=line_2.front();
//				printP(line_2.front());c++;line_2.pop();secondTime = secondCpu;}}	else if(!line_3.empty()) //在第三个队列执行 {while(secondTime>0){line_3.front().need_time--;thirdTime--;currentTime++;while(number<num&&process[number].arrive_time==currentTime){line_1.push(process[number++]);}if(line_3.front().need_time==0)break;}	if(line_3.front().need_time>0){line_3.push(line_3.front());line_3.pop();thirdTime = thirdCpu;}else{firstTime = firstCpu;line_3.front().run_time=currentTime - line_3.front().begin_time;line_3.front().end_time=currentTime;finish[c]=line_3.front();c++;line_3.pop();}}cout<<line_1.empty()<<line_2.empty()<<line_3.empty()<<endl;if (line_1.empty()&&line_2.empty()&&line_3.empty()&&currentTime<process[number].arrive_time){currentTime = process[number].arrive_time;}				}	
}int main()
{queue<Process> line_1; //定义第一个优先级队列queue<Process> line_2; //定义第二个优先级队列queue<Process> line_3; //定义第三个优先级队列Input();sort(process,process+num,cmp);Running(line_1,line_2,line_3);double sum=0;double sum2=0;cout<<"进程名称"<<" 开始时间"<<" 结束时间"<<" 运行时间"<<" 带权周转时间"<<endl;for(int i=0;i<num;i++){sum+=double(finish[i].end_time-finish[i].arrive_time)/double(finish[i].Need_time);sum2+=double(finish[i].end_time-finish[i].arrive_time);printP(finish[i]);}cout<<"平均周转时间:"<<sum2/num;cout<<"平均带权周转时间:"<<sum/num<<endl;cout<<"written by zzdxls"<<endl;
}

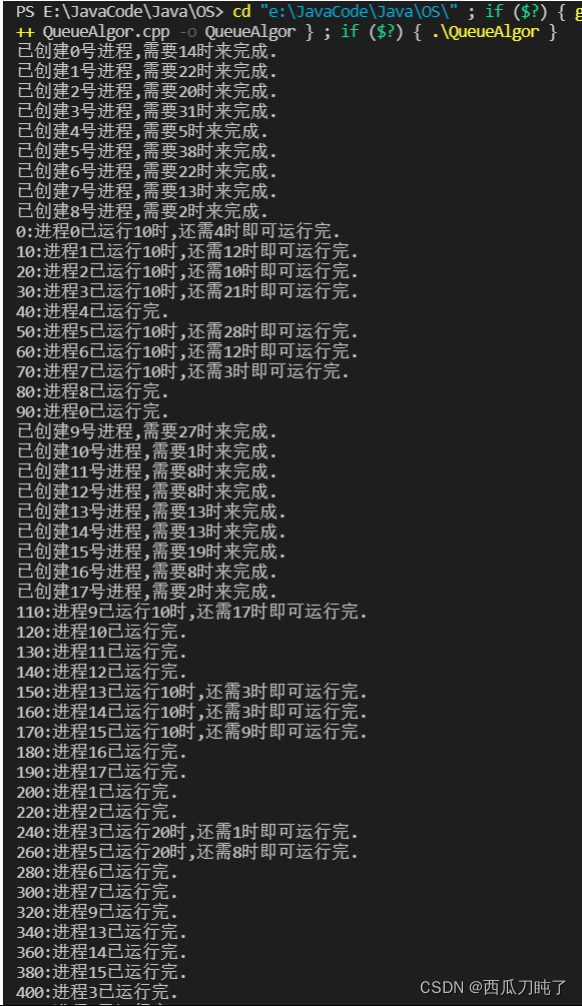
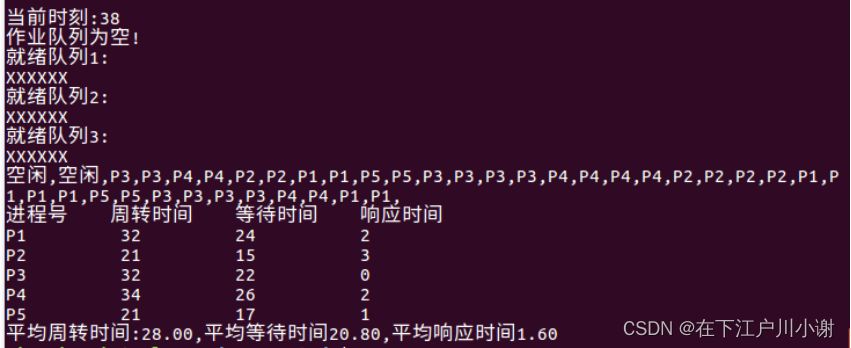
运行结果