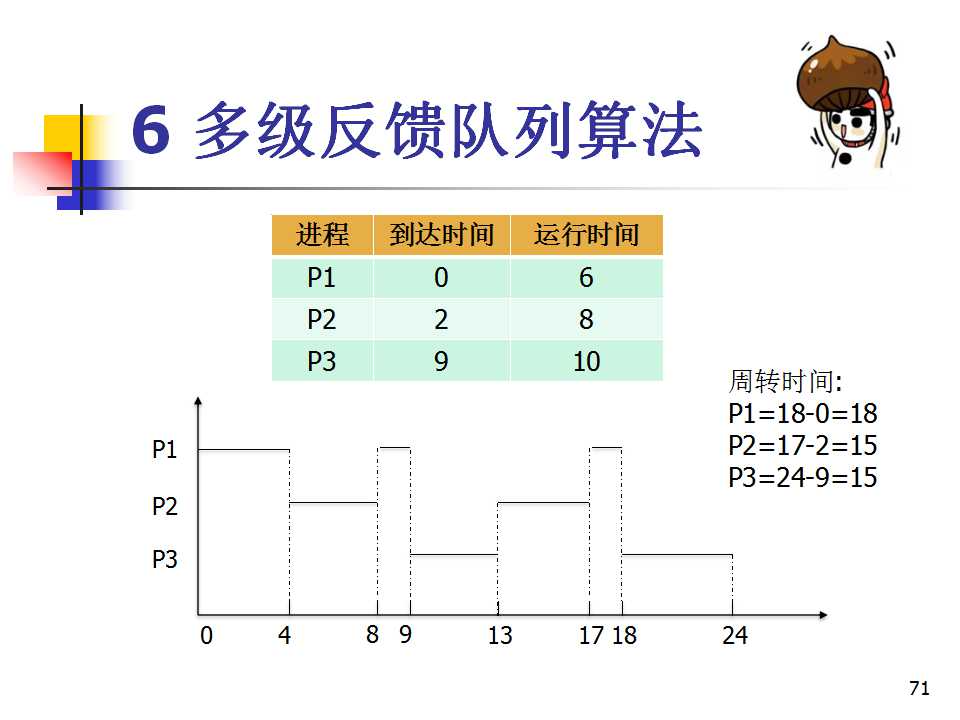
计操实验 多级反馈队列C语言
需求:
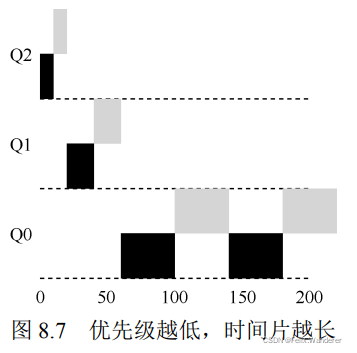
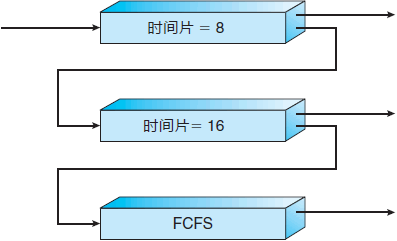
1.队列4级,每一级的队列长度均为10;第一级的时间片为T,第二级的时间片为2T,第三级的时间片为4T,第四级的时间片为8T;(T的大小自己定)
2.非立即抢占的剥夺式调度算法;
3.要有:在调度高级别队列时,有新来的进程进入系统。
流程图:
代码如下:
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define T 1typedef struct Node
{int ArrivalTime; //到达时间 int WorkTime; //服务时间 int number; //到达顺序 int flag; //0等待,1运行完成 struct Node *next;
}Process;
typedef struct QueueList
{int TimeSlice; //时间片 int length; //队列长度 Process *front; //队列第一个进程指针 struct QueueList *next;
}Queue;Queue *head = NULL;
Process *Finish = NULL; //已完成
int time = 0;void InitQueue()
{Queue *temp;for(int i=0;i<4;i++){temp = (Queue*)malloc(sizeof(Queue));temp->front = NULL;temp->TimeSlice = pow(2,i)*T;temp->length = 10;temp->next = NULL;if(head == NULL){head = temp;temp = NULL;}else{Queue *temp2;temp2 = head;while(temp2->next != NULL){temp2 = temp2->next;}temp2->next = temp;temp = NULL;}}
}
void InitProcess()
{int num;printf("请输入进程数量:"); scanf("%d",&num);if(num > 10){printf("超过队列长度!"); exit(1);}Process *temp;for(int i=0;i<num;i++){temp = (Process*)malloc(sizeof(Process));printf("请输入第%d个进程的到达时间及服务时间:",i+1);scanf("%d %d",&temp->ArrivalTime,&temp->WorkTime);temp->flag = 0;temp->next = NULL;temp->number = i+1;if(head->front == NULL){temp->next = NULL;head->front = temp;}else{Process *temp2;temp2 = head->front;while(temp2->next != NULL){temp2 = temp2->next;}temp->next = NULL;temp2->next = temp;}}
}void Insert2NextQueue(Process *P,Queue *Q)
{//将进程P插入Q队尾 if(Q->front == NULL){P->next = NULL;Q->front = P;}else{Process *temp;temp = Q->front;while(temp->next != NULL){temp = temp->next;}P->next = NULL;temp->next = P;}
}void RunFirstProcess(Queue *Q)
{if(Q->front->WorkTime <= Q->TimeSlice){time += Q->front->WorkTime;Q->front->WorkTime = 0;Q->front->flag = 1;printf("t=%d时刻:第%d个进程运行结束\n",time,Q->front->number);Process *temp,*temp2;temp = Finish;temp2 = Q->front->next;if(Finish == NULL){Finish = Q->front;Finish->next = NULL;}else{while(temp->next != NULL){temp = temp->next;}Q->front->next = NULL;temp->next = Q->front; }Q->front = temp2;}else{Q->front->WorkTime -= Q->TimeSlice;time += Q->TimeSlice;Process *temp,*temp2;temp = Q->front;temp2 = Q->front->next;if(Q->next != NULL){Insert2NextQueue(temp,Q->next);Q->front = temp2; }else{//Insert2NextQueue(Q->front,Q); if(temp2 != NULL){Q->front = temp2;if(temp2->next != NULL){temp2 = temp2->next;}temp2->next = temp;temp->next = NULL;}}}}void MLFQ()
{Queue *Q1=head;Queue *Q2=Q1->next;Queue *Q3=Q2->next;Queue *Q4=Q3->next; while(1){if(Q1->front != NULL && time >= Q1->front->ArrivalTime){//Q1取第一个进程运行 RunFirstProcess(Q1);}else{if(Q2->front != NULL && time >= Q2->front->ArrivalTime){//Q2取第一个进程运行 RunFirstProcess(Q2);}else{if(Q3->front != NULL && time >= Q3->front->ArrivalTime){//Q3取第一个进程运行RunFirstProcess(Q3); }else{if(Q4->front != NULL && time >= Q4->front->ArrivalTime){//Q4取第一个进程运行RunFirstProcess(Q4); }else{if(Q1->front != NULL || Q2->front != NULL || Q3->front != NULL || Q4->front != NULL){time++;}else{printf("所有进程运行完毕");}break; }}}}}
}int main()
{InitQueue();InitProcess();MLFQ();return 0;
}