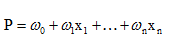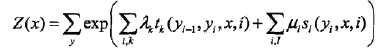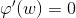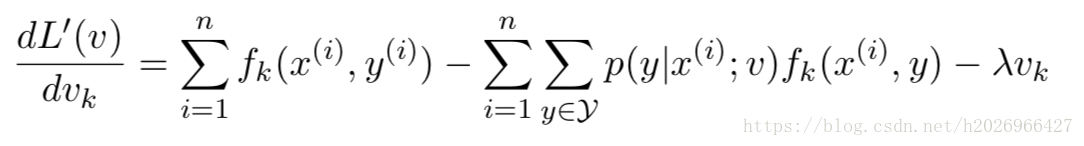常用的三个线性模型的原理及python实现——线性回归（Linear Regression）、对数几率回归（Logostic Regression）、线性判别分析（Linear Discriminant）。 这可能会是对线性模型介绍最全面的博客

一、线性模型 （Linear Model）

对于一个具有d个属性的对象来说，我们可以用下面这一组向量描述

向量中的每个值都是对象一个属性的值，由上可以看出，线性模型是一个通过属性的线性组合来进行对象判定的函数，即

用向量的形式可以写成

其中

当求得w与b后，线性模型就得以确定。线性模型是最简单也是最常用的模型之一，同时，很多更为强大的非线性模型也是由线性模型发展来的，所以，了解掌握线性模型十分必要

二、线性回归 （Linear Regression）

线性回归是指，模型试图学得

求解模型的关键在于，如何求得w与b，解决问题的落点在于，如何衡量f(x)与y 差距，通常我们使用均方误差来衡量这种差距的大小，即

均方差有非常良好的几何意义，它对应了常用的欧几里得距离即“欧式距离”。基于均方误差最小化的原理来求解模型的方法叫做“最小二乘法”（least square method），在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小，现令

将其对w和b分别求导，并令其导数为0，可得

对于更一般的情形，若样本由d个属性描述，此时我们应当求解

这就是我们通常所说的多元线性回归（multivariate linear regression）
现在利用最小二乘法对w和b进行估计。将w和b统一记为

同时也把数据集D表示为一个 *m x (d + 1)*的矩阵 X

将标记也写成向量形式

此时的求解方程可以写为

用上式对w进行求导，当X 的转置与其相乘为满秩矩阵或者正定矩阵时，令导数为0可得

最终得到的多元线性回归模型如下

基于上述理论，其python源码如下：

'''
1.using least square method figure out linear regression
'''
import numpy as np
import matplotlib.pyplot as pltdef linear_regression(x,y):     def preprocess(x):X = np.mat(x)b = np.mat([1]*len(x))X = np.hstack((X,b.T))return Xdef cal_w(x,y):X = preprocess(x)Y = np.mat(y).Treturn (X.T*X).I*X.T*Y     return preprocess(x)*cal_w(x,y),cal_w(x,y).tolist()

其测试代码如下（注本文所有的代码原为一个文件，运行时，请完整复制全部代码）

#visiable and output test
x = [[0.697,0.460],[0.774,0.376],[0.634,0.264],[0.608,0.318],[0.556,0.215],[0.403,0.237],[0.481,0.149],[0.437,0.211],[0.666,0.091],[0.243,0.267],[0.245,0.057],[0.343,0.099],[0.639,0.161],[0.657,0.198],[0.360,0.370],[0.593,0.042],[0.719,0.103]]
y = [1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0]
yy,w = linear_regression(x,y)
i,x1,x2 = 0,[],[]
while i < len(x):x1.append(x[i][0])x2.append(x[i][1])i += 1i = 0
plt.figure(1)
plt.subplot(121)
plt.title('linear regression')
while i < len(x1):if y[i] == 0:plt.scatter(x1[i],x2[i],color = 'r')elif y[i] == 1:plt.scatter(x1[i],x2[i],color = 'g')i += 1
a = -(w[2][0]/w[1][0])
b = -(w[0][0]+w[2][0])/w[1][0]
plt.plot([0,1],[a,b])

三、对数几率回归（Logistic Regression）

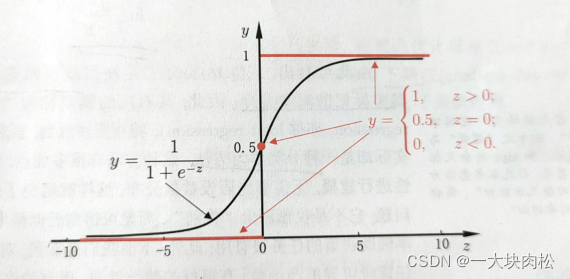
对数几率回归实质上使用Sigmoid函数对线性回归的结果进行了一次非线形的转换，Sigmoid函数如下

将线性模型带入可得

该式实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率，因此，其对应的模型称为“对数几率回归”（logistic regression），将上式取常用对数，可转化为

现在我们开始对w和b进行估计，将上式中的y视为类后验概率估计

则可以将模型转化为

显然有

到这里，我们便可以使用“极大似然法”（maximum likelihood method）来估计w和b，给定数据集如下

对率回归模型最大化“对数似然”,记为式 1

即令每个样本属于其真实标记的概率越大越好，现令

再令

此时，便可将之前式1里的似然项改写为

由此可知，式1等于

这是一个高阶可导连续凸函数，接下来给出牛顿法的推导公式，首先为
设置任意值
设定允许误差，再代入下式循环求解求解

其中

基于上述理论，其python源码如下：

'''
2.Newton method figure out logistic regression
'''def logistic_regression(x,y,error,n):def preprocess(x,y):X = np.mat(x)b = np.mat([1]*len(x))X = np.hstack((X,b.T))w = [1]*(len(x[0])+1)W = np.mat(w).TY = yreturn X,W,Y   def func_p(X,W):a = (X*W).tolist()b = float(a[0][0])temp = np.exp(b)/(1+np.exp(b))return tempdef dfunc(X,Y,W):i,num,sum1 = 0,len(X),0while i < num:temp = Y[i] - func_p(X[i],W)sum1 += X[i]*tempi += 1return sum1*(-1)def d2func(X,Y,W):i,num,sum1 = 0,len(X),0while i < num:         temp = func_p(X[i],W)*(1 - func_p(X[i],W))sum1 += X[i]*(X[i].T)*tempi += 1sum1 = sum1.tolist()return float(sum1[0][0])def Newton(x,y,error,n):X,W,Y = preprocess(x,y)i = 1while i < n:d1 = dfunc(X,Y,W)a = (d1*d1.T).tolist()a = float(a[0][0])if a < error:return Wbreaktemp = dfunc(X,Y,W)W = W - temp.T*(d2func(X,Y,W)**(-1))i += 1if i == n:return 'error'w = Newton(x,y,error,n)X,W,Y = preprocess(x,y)yy = (X*w).tolist()w = w.tolist()return w,yy

测试代码如下

#visiable and output test           
w,yy = logistic_regression(x,y,0.0001,1000)i,x1,x2,z = 0,[],[],[]
while i < len(x):x1.append(x[i][0])x2.append(x[i][1])z.append(yy[i][0])i += 1i = 0plt.subplot(122)
plt.title('logistic regression')
while i < len(x1):if y[i] == 0:plt.scatter(x1[i],x2[i],color = 'r')elif y[i] == 1:plt.scatter(x1[i],x2[i],color = 'g')i += 1
a = -(w[2][0]/w[1][0])
b = -(w[0][0]+w[2][0])/w[1][0]
plt.plot([0,1],[a,b])

四、线性判别分析（Linear Discriminant Analysis）

线性判别分析是一种经典的线形学习方法，最早由费舍尔（Fisher）在二分类问题上提出，所以也称为“Fisher判别分析”
其思想非常朴素：给定训练样例集，设法将样例点投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对测试样例进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。这里只讲述二分类问题的原理和求解，给定数据集

再分别令

表示i（等于0或1）类示例的集合、均值向量、协方差矩阵，将数据投影到直线w上，则两类样本的中心在直线上的投影分别为

若将所有样本点都投影到直线上，则两类样本的协方差分别为

想要使同类样例的投影点尽可能接近，可以让同类样例的协方差尽可能小，即

尽可能小；同时，也想要让异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大，即

尽可能的大，则可以定义最大化目标

定义类内散度矩阵（within class scatter matrix）

以及类间散度矩阵（between class）

可将最大化目标重写为

由拉格朗日乘法子可从上式求出

由此可解出二分类问题的LDA模型，基于上述理论，其python源码如下：

'''
3.Linear Discriminant Analysis for binary classification problem
'''def LDA(x,y):def preprocess(x,y):i = 0X0,X1 = [],[]while i < len(y):if y[i] == 0:X0.append(x[i])elif y[i] == 1:X1.append(x[i])i += 1return X0,X1def average(X):X = np.mat(X)i = 1while i < len(X):X[0] = X[0] + X[i]i += 1res = X[0]/ireturn resdef Sw(X0,X1,u0,u1):X_0 = np.mat(X0)X_1 = np.mat(X1)Sw0,i = 0,0temp0 = (X_0 - u0).T*((X_0 - u0))
#        while i < len(temp0):
#            Sw0 += float(temp0[i,i])
#            i += 1
#        Sw1,i = 0,0temp1 = (X_1 - u1).T*((X_1 - u1))
#        while i < len(temp1):
#            Sw1 += float(temp1[i,i])
#            i += 1
#        return Sw0+Sw1return temp0 + temp1X0,X1 = preprocess(x,y)u0,u1 = average(X0),average(X1)SW = Sw(X0,X1,u0,u1)return (SW**(-1)*numpy.mat(u0-u1).T).tolist()   #visiable and output test           
W = LDA(x,y)i,x1,x2,z = 0,[],[],[]
while i < len(x):x1.append(x[i][0])x2.append(x[i][1])i += 1
i = 0
plt.figure(2)
plt.subplot(121)
plt.title('LDA')
while i < len(x1):if y[i] == 0:plt.scatter(x1[i],x2[i],color = 'r')elif y[i] == 1:plt.scatter(x1[i],x2[i],color = 'g')i += 1
print(W)plt.plot([0,-W[0][0]],[0,-W[1][0]])

五、三个模型结果对比图

完整代码地址：https://github.com/LiangjunFeng/Machine-Learning/blob/master/1.linear_model.py

六、更多资源下载

微信搜索“老和山算法指南”获取更多下载链接与技术交流群

有问题可以私信博主，点赞关注的一般都会回复，一起努力，谢谢支持。