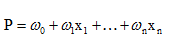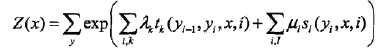---

一、泊松回归（Poisson regression）简介

（一）泊松回归

在统计学中，泊松回归是回归分析的广义线性模型形式，用于对计数数据和列联表进行建模。泊松回归假设响应变量Y具有泊松分布，并假设其期望值的对数可以通过未知参数的线性组合来建模。泊松回归模型有时被称为对数线性模型，尤其是在用于对列联表建模时。

负二项式回归（Negative binomial regression） 是泊松回归的一种流行推广，因为它放松了方差等于泊松模型做出的均值的高度限制性假设。传统的负二项式回归模型基于泊松-伽马混合分布。该模型很受欢迎，因为它使用伽马分布对泊松异质性进行建模。

如上图，左侧的模型是线性回归，表示对于 X 的每个水平，响应大致是正常的。

右侧的模型是泊松回归模型，表示对于 X 的每个水平，响应遵循泊松分布。

（二）计数数据

计数数据 也可以表示为 速率数据，因为事件在一个时间范围内发生的次数可以表示为原始计数（即“一天中，我们吃三顿饭”）或速率（“我们吃0.125 餐/小时”）

计数数据的特征：

• 整数数据： 数据由非负整数组成，回归技术（例如普通最小二乘回归）可能不适合对此类数据建模。
• 偏态分布： 数据可能仅包含几个值的大量数据点，从而使频率分布非常偏斜。
• 稀疏性： 数据可能反映诸如伽马射线暴等罕见事件的发生，从而使数据稀疏。
• 发生率： 为了创建模型，可以假设有一定的事件发生率λ驱动此类数据的生成，事件率可能会随着时间而漂移。

例如：布鲁克林大桥上骑自行车人数的时序图

（三）泊松分布

1）数学表达式

泊松分布是一种以法国数学家西蒙·丹尼斯·泊松命名的统计理论。它模拟事件或事件 y 在特定时间范围内发生的概率，假设 y 的发生不受 y先前发生的时间的影响。这可以使用以下数学公式表示：

这里， λ 是每单位曝光可能发生的事件的平均次数 ，也称为泊松分布的参数。暴露可能是时间、 空间、人口规模、距离或面积，但通常是时间，用 t表示。如果未给出暴露值，则假定它等于 1。

2）不同λ的泊松分布图

# vector of colors
colors <- c("Red", "Blue", "Gold", "Black", "Pink", "Green")
# declare a list to hold distribution values
poisson.dist <- list()a <- c(1, 2, 3, 4, 5, 6) # A vector for values of u
for (i in 1:6) {poisson.dist[[i]] <- c(dpois(0:20, i)) # Store distribution vector for each corresponding value of u
}
# plot each vector in the list using the colors vectors to represent each value for u
plot(unlist(poisson.dist[1]), type = "o", xlab="y", ylab = "P(y)",col = colors[i])
for (i in 1:6) {lines(unlist(poisson.dist[i]), type = "o", col = colors[i])
}
# Adds legend to the graph plotted
legend("topright", legend = a, inset = 0.08, cex = 1.0, fill = colors, title = "Values of λ")

结果如下：

（四）泊松回归模型

泊松回归模型的工作是通过链接函数将观察到的计数y拟合到回归矩阵X，该链接函数将速率向量λ表示为 ：

1. 回归系数β
2. 回归矩阵X的函数

将λ与X连接起来的良好链接函数f (.)可能是什么？事实证明，以下指数链接函数效果很好：

即使回归量X或回归系数β具有负值，此链接函数也保持λ非负值。这是基于计数的数据的要求。

一般来说，我们有：

二、R语言实例分析

例1. Breslow癫痫数据分析

使用robust包中的Breslow癫痫数据（Breslow,1993）来讨论在治疗初期的八周内，抗癫痫药物对癫痫发病数的影响。

就遭受轻微或严重间歇性癫痫的病人的年龄和癫痫发病数收集了数据，包含病人被随机分配到药物组或者安慰剂组前八周和随机分配后八周两种情况。响应变量为sumY（随机化后八周内癫痫发病数），预测变量为治疗条件（Trt）、年龄（Age）和前八周内的基础癫痫发病数（Base）。之所以包含基础癫痫发病数和年龄，是因为它们对响应变量有潜在影响。在解释这些协变量后，我们感兴趣的是药物治疗是否能减少癫痫发病数。

install.packages("robust")
library(robust)
data(breslow.dat, package="robust")
names(breslow.dat)
summary(breslow.dat[c(6,7,8,10)])

数据集的统计汇总信息：

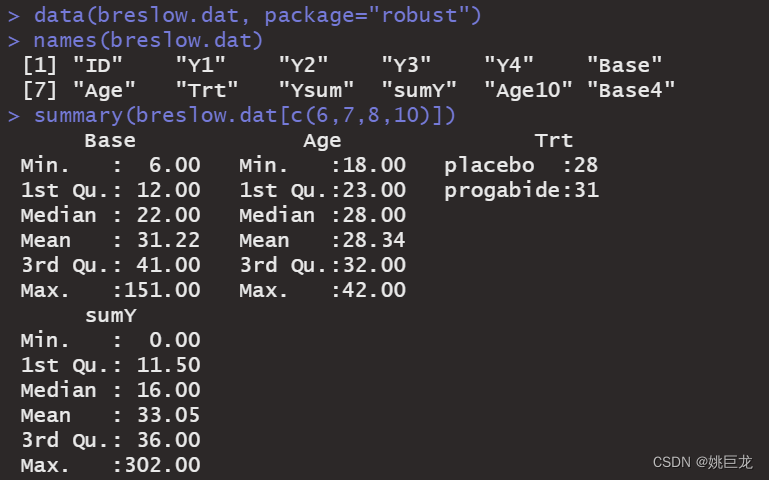
虽然数据集有12个变量，但是我们只关注之前描述的四个变量。基础和随机化后的癫痫发病数都有很高的偏度。现在，我们更详细地考察响应变量。

opar <- par(no.readonly = TRUE)
par(mfrow=c(1,2))
attach(breslow.dat)
hist(sumY, breaks = 20, xlab = "Seizure Count",main = "Distribution of Seizures")
boxplot(sumY~Trt, xlab = "Treatment", main="Group Comparison")
par(opar)

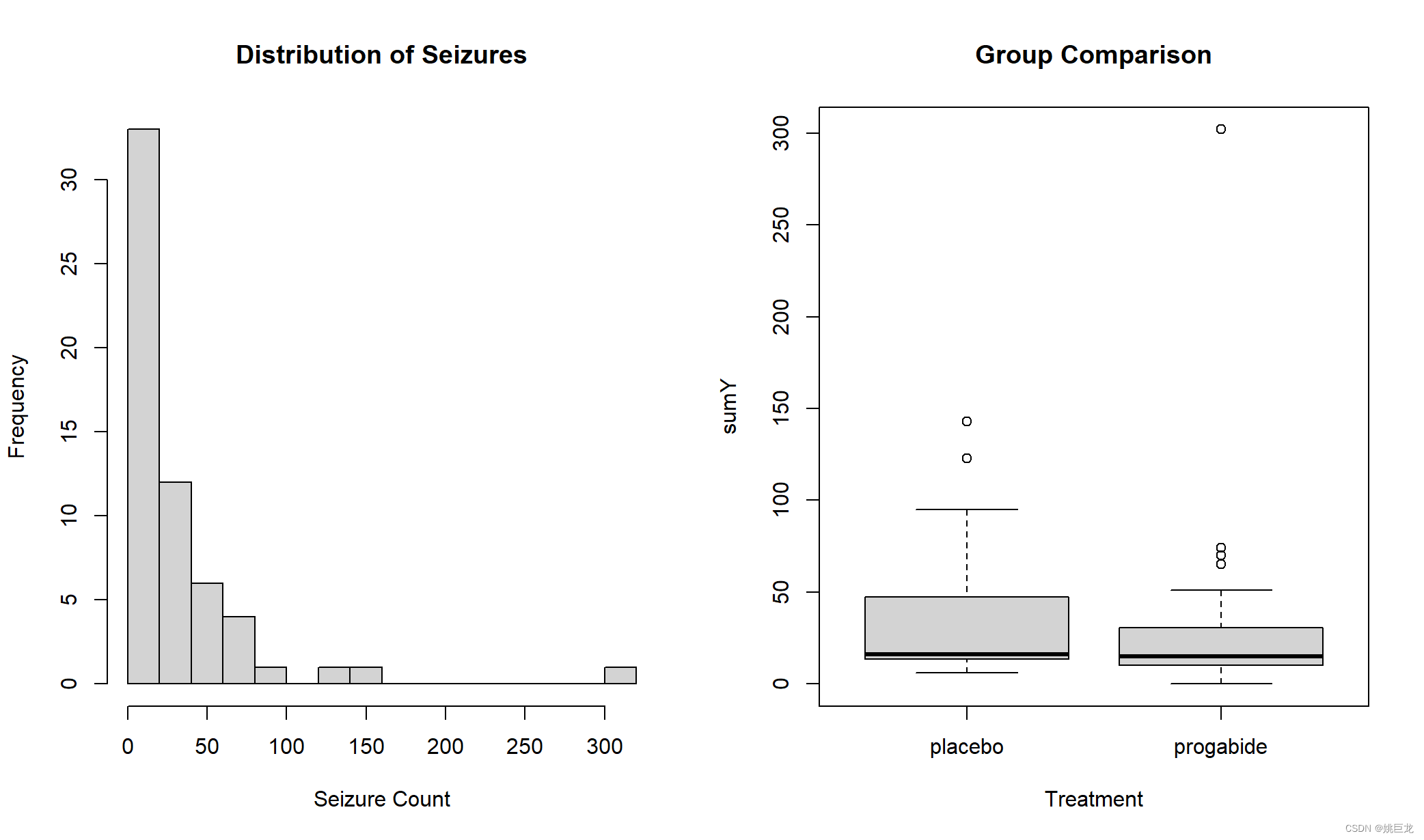
从图中可以清楚地看到因变量的偏倚特性以及可能的离群点。初看图形时，药物治疗下癫痫发病数似乎变小了，且方差也变小了（泊松分布中，较小的方差伴随着较小的均值）。与标准最小二乘回归不同，泊松回归并不关注方差异质性。

接下来拟合泊松回归：

fit <- glm(sumY~Base+Age+Trt, data = breslow.dat, family = poisson())
summary(fit)

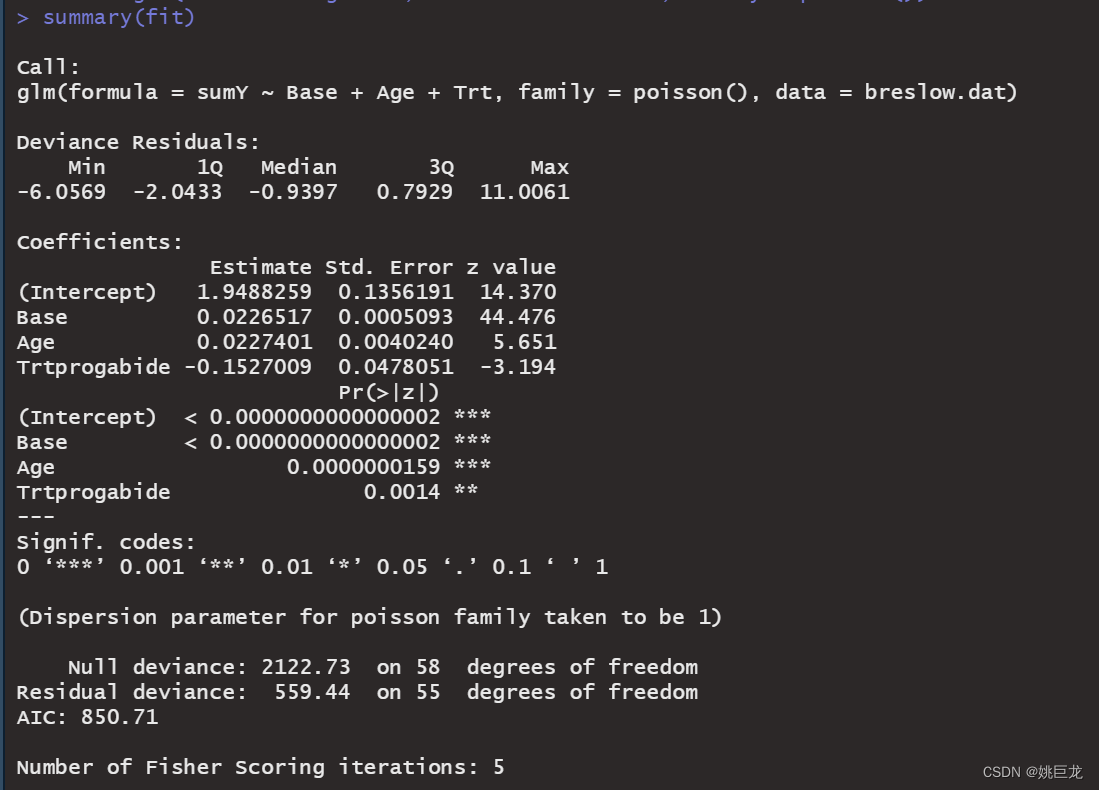
输出结果列出了偏差、回归参数、标准误和参数为0的检验。注意，此处预测变量在p＜0.05的水平下都非常显著。

使用coef()函数可获取模型系数，或者调用summary()函数的输出结果中的Coefficients表格：

coef(fit)
exp(coef(fit))
deviance(fit)/df.residual(fit)

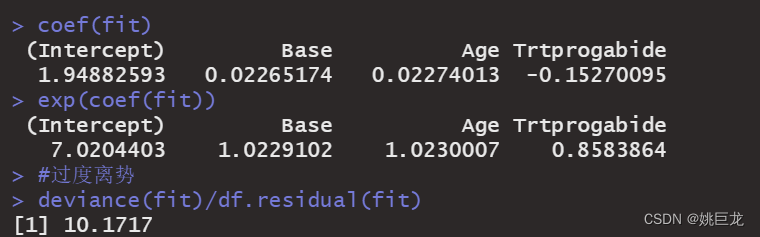
在泊松回归中，因变量以条件均值的对数形式loge(λ)来建模。年龄的回归参数为0.0227，表明保持其他预测变量不变，年龄增加一岁，癫痫发病数的对数均值将相应增加0.03。截距项即当预测变量都为0时，癫痫发病数的对数均值。由于不可能为0岁，且调查对象的基础癫痫发病数均不为0，因此本例中截距项没有意义。

通常在因变量的初始尺度（癫痫发病数，而非发病数的对数）上解释回归系数比较容易。为此，指数化系数，可以看到，保持其他变量不变，年龄增加一岁，期望的癫痫发病数将乘以1.023。这意味着年龄的增加与较高的癫痫发病数相关联。更为重要的是，一单位Trt的变化（即从安慰剂到治疗组），期望的癫痫发病数将乘以0.86，也就是说，保持基础癫痫发病数和年龄不变，服药组相对于安慰剂组癫痫发病数降低了20%。

library(qcc)
qcc.overdispersion.test(breslow.dat$sumY, type="poisson")

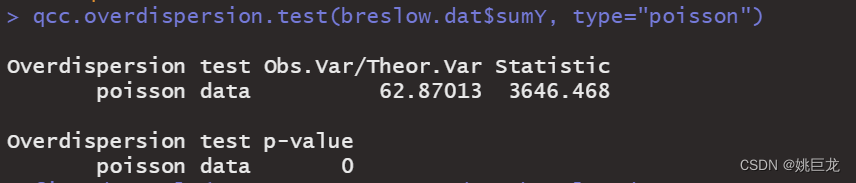
过度离势

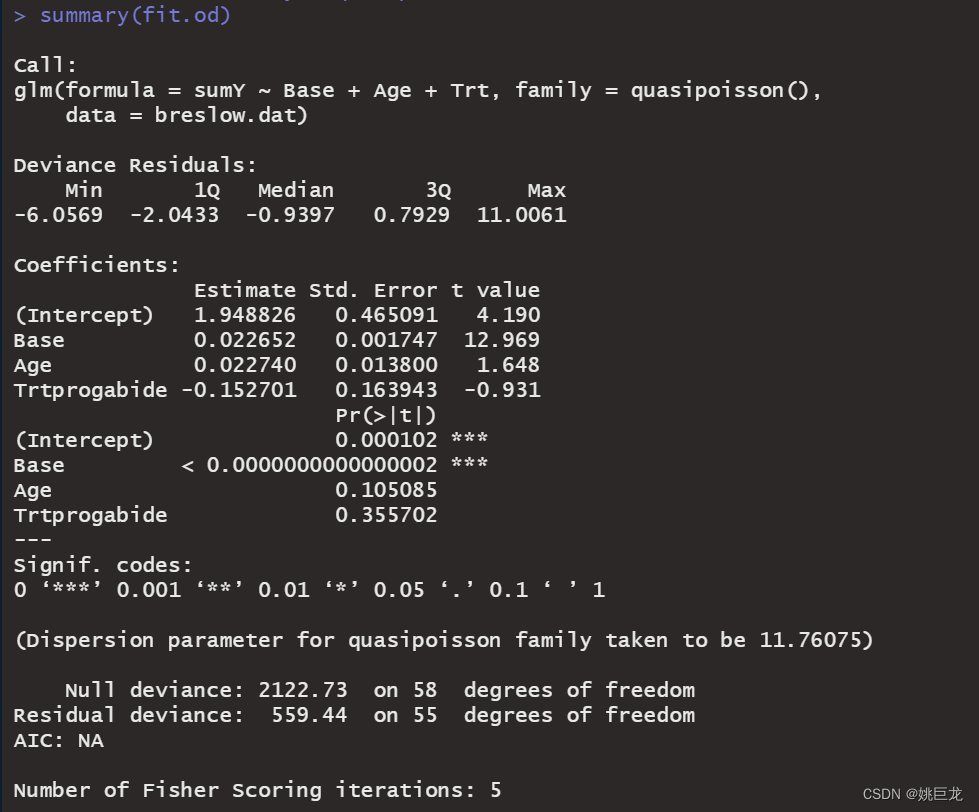
泊松分布的方差和均值相等。当响应变量观测的方差比依据泊松分布预测的方差大时，泊松回归可能发生过度离势。处理计数型数据时经常发生过度离势，且过度离势会对结果的可解释性造成负面影响，因此我们需要花些时间讨论该问题。

fit.od <- glm(sumY~Base+Age+Trt, data=breslow.dat,family = quasipoisson())
summary(fit.od)