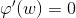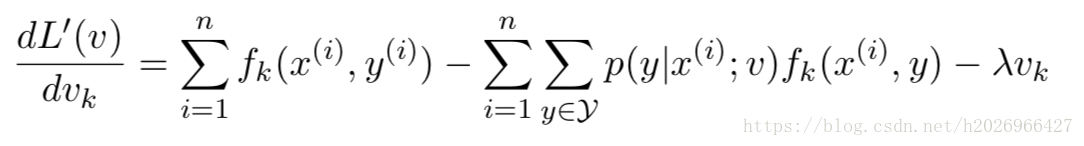多级队列调度和多级反馈队列调度算法的实现

article/2025/8/15 13:54:34

多级队列调度算法

操作系统实验导航
实验一：银行家算法 https://blog.csdn.net/weixin_46291251/article/details/115384510
实验二：多级队列调度和多级反馈队列调度算法 https://blog.csdn.net/weixin_46291251/article/details/115530582
实验三：动态分区式内存管理 https://blog.csdn.net/weixin_46291251/article/details/115772341
实验四：Linux下多进程通信 https://blog.csdn.net/weixin_46291251/article/details/116274665
实验五：进程通信的三种方式 https://blog.csdn.net/weixin_46291251/article/details/116301250
实验六：Linux文件系统实验 https://blog.csdn.net/weixin_46291251/article/details/116423798
实验七：自制简单U盘引导程序 https://blog.csdn.net/weixin_46291251/article/details/116427629
实验八：磁盘调度算法 https://blog.csdn.net/weixin_46291251/article/details/116431907
实验九：请求分页系统中的置换算法 https://blog.csdn.net/weixin_46291251/article/details/116443021
学习笔记：操作系统复习笔记 https://blog.csdn.net/weixin_46291251/article/details/117086851

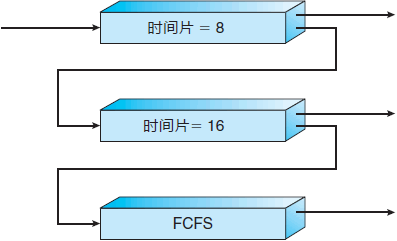
  • 多级队列：该算法将系统中的进程就绪队列从一个拆分为若干个，将不同类型或性质的进程固定分配在不同的就绪队列，不同的就绪队列采用不同的调度算法，一个就绪队列中的进程可以设置不同的优先级，不同的就绪队列本身也可以设置不同的优先级。
    多级队列调度算法由于设置多个就绪队列，因此对每个就绪队列就可以实施不同的调度算法，因此，系统针对不同用户进程的需求，很容易提供多种调度策略。

题目描述：

  • 设RQ分为RQ1和RQ2
  • RQ1采用轮转法，时间片q=7.
  • RQ1>RQ2
  • RQ2采用短进程优先调度算法。
  • 测试数据如下：
  • 其中：RQ1: P1-P5,   RQ2: P6-P10　
进程P1P2P3P4P5P6P7P8P9P10
运行时间1611141315211810714
已等待时间6543212345

程序功能

  • 对于给定的数据使用多级队列调度算法进行分析计算周转时间。其中多级队列分为RQ1和RQ2 ，RQ1采用的是时间片长度为7的时间片轮转算法，RQ2采用的是短进程优先算法。并且RQ1的优先级高于RQ2（即只有在RQ1内所有程序运行结束，RQ2才能开始运行）

设计思路

  • 时间片轮转：首先对RQ1按照等待时间长短排序，然后从头设置循环，只要队列不空就一直进行下去，每次取队头RQ1的下一个元素（RQ1仅用作标志，不存储数据）判断need是否小于等于时间片大小，小于等于则置为0后踢出队列进入finish队列，大于则将need减去时间片大小，然后将其移动至队尾。
  • 短进程优先：开始前需要对RQ2按照剩余执行时间大小进行排序，与时间片轮转法类似，不同的是这里一旦开始执行就直接执行完毕，然后下一个进程上处理机运行。

数据结构

  • 本程序每个进程用一个PCB表示，每个PCB内含有name（标识符）、need（当前仍然需要多长时间才能运行结束）、turn（周转时间（等于等待时间+运行时间））、next指针（指向等待队列的下一个进程）。两个队列的头节点分别为RQ1、RQ2还有一个结束队列Finish（运行结束后进程从原队列进入这里）
typedef struct tag_pcb {char name[8];int need = 0;//需要运行的时间int turn = 0;//周转时间=等待时间+运行时间struct tag_pcb* next = NULL;
}PCB;
PCB* RQ1=new PCB, * RQ2 = new PCB, * Finish = new PCB;

代码实现：

#include<iostream>
#include <fstream>
using namespace std;typedef struct tag_pcb {char name[8];int need = 0;//需要运行的时间int turn = 0;//周转时间=等待时间+运行时间struct tag_pcb* next = NULL;
}PCB;
PCB* RQ1=new PCB, * RQ2 = new PCB, * Finish = new PCB;
const int TimePiece = 7;//时间片长度void ReadFile(){ifstream In("RQ1.txt");PCB* Current = RQ1;while (!In.eof()) {PCB* Cur = new PCB;In >> Cur->name >> Cur->need>> Cur->turn;Current->next = Cur;Current = Current->next;}In.close();ifstream In1("RQ2.txt");PCB* Current1 = RQ2;while (!In1.eof()) {PCB* Cur1 = new PCB;In1 >> Cur1->name >> Cur1->need >> Cur1->turn;Current1->next = Cur1;Current1 = Current1->next;}In1.close();
}void Q1_Insert(PCB a) { //时间片轮转算法队列的插入(插入尾部)PCB* Current = RQ1;while (Current->next != NULL)Current = Current->next;Current->next = new PCB;*Current->next = a;//Current->next = &a;Current->next->next = NULL;}
void Q2_Insert(PCB b) { //短进程优先调度算法队列的插入PCB* Current = RQ2;while (Current->next != NULL)Current = Current->next;Current->next = new PCB;*Current->next = b;Current->next->next = NULL;}
void Fin_Insert(PCB c) { //短进程优先调度算法队列的插入PCB* cc = new PCB;*cc = c;cc->next = Finish->next;Finish->next = cc;   
}
void Q2_sort(PCB *T) {PCB* X = new PCB;//用来保存排序后的链表PCB* p = new PCB;//用来保存当此最小值的前一位PCB* Current = T->next;PCB * PreCurrent = T;PCB* TailX = X;while (T->next != NULL) {int tem = 999999;Current = T->next;PreCurrent = T;while (Current != NULL) {if (Current->need < tem) {tem = Current->need;p = PreCurrent;//cout << "处理" << p->name << p->need << "\n";}Current = Current->next;PreCurrent = PreCurrent->next;}TailX->next = p->next;TailX = TailX->next;if (p->next->next != NULL)p->next = p->next->next;elsep->next = NULL;      }*T = *X;
}int main()
{ReadFile();int clock = 0; //时钟while (RQ1->next != NULL) {//表示RQ1还有元素int t = TimePiece;PCB* Current = RQ1->next;int fin = 0;if (Current->need <= t)t = Current->need, fin = 1;clock += t;//表示pi运行t//输出计算过程//cout << "\n" << Current->name << "_____" << Current->turn << "__+ ___" << clock << "__= ___" << Current->turn +clock << "\n";Current->need -= t;if (fin)Current->turn += clock, Fin_Insert(*Current);//运行结束    elseQ1_Insert(*Current);//进入队尾等待运行if (Current->next == NULL)break;RQ1->next = Current->next;}clock = 0;//时钟要清空一次Q2_sort(RQ2);//先排序cout << "RQ2:__"; for (PCB* Current2 = RQ2->next; Current2 != NULL; Current2 = Current2->next)cout << Current2->name << "--";while (RQ2->next != NULL) {//表示RQ2还有元素(到这一步默认RQ1已经为空)PCB* Current3 = RQ2->next;int t = Current3->need;clock += t;//表示pi运行tCurrent3->need -= t;//实质为清空Current3->turn += clock;Fin_Insert(*Current3);if (Current3->next == NULL)break;RQ2->next = Current3->next;}int SUM = 0;for (PCB* Current2 = Finish->next; Current2 != NULL; Current2 = Current2->next) {cout << "\n" << Current2->name <<"\t"<< Current2->turn ;SUM += Current2->turn;}cout << "\n总周转时间为：" << SUM << "\n";
}
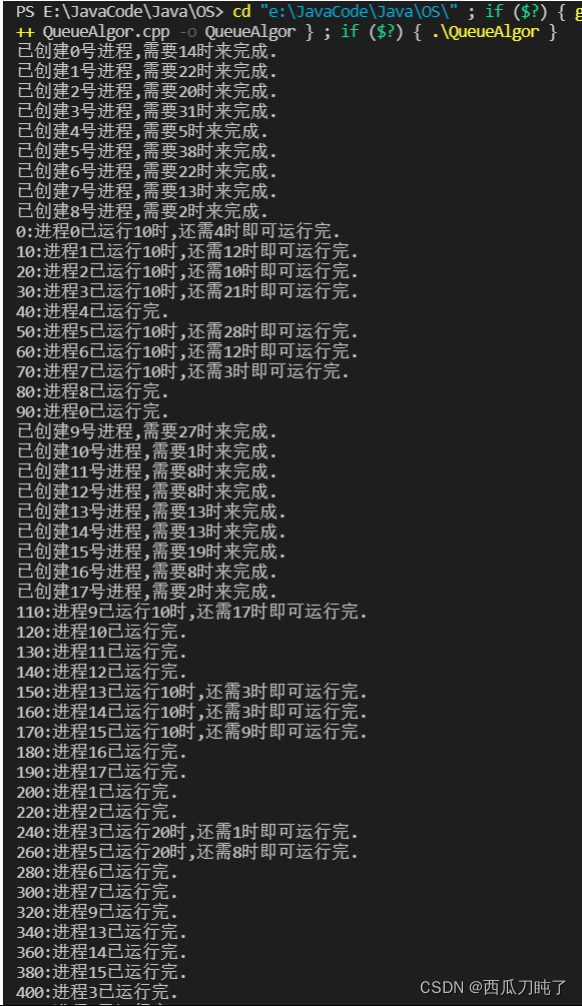
  • 多级队列调度测试结果：
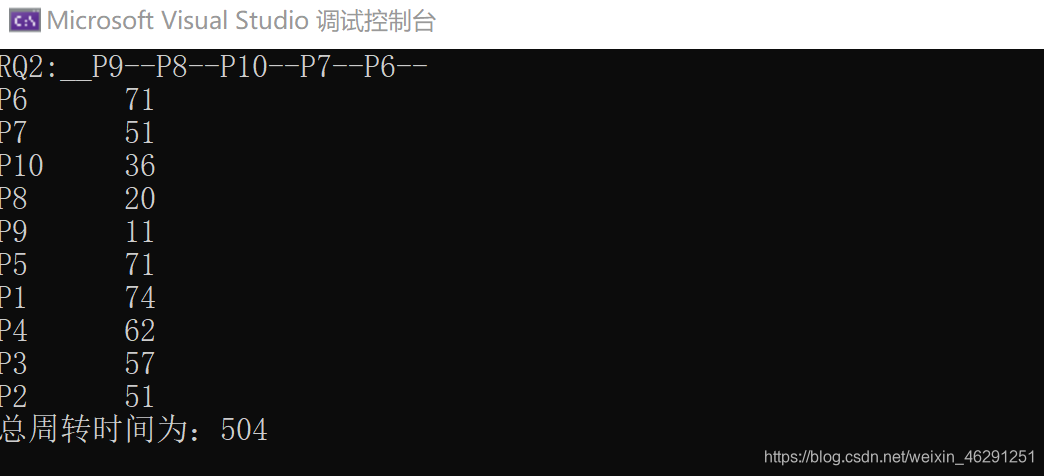
    在这里插入图片描述

附：

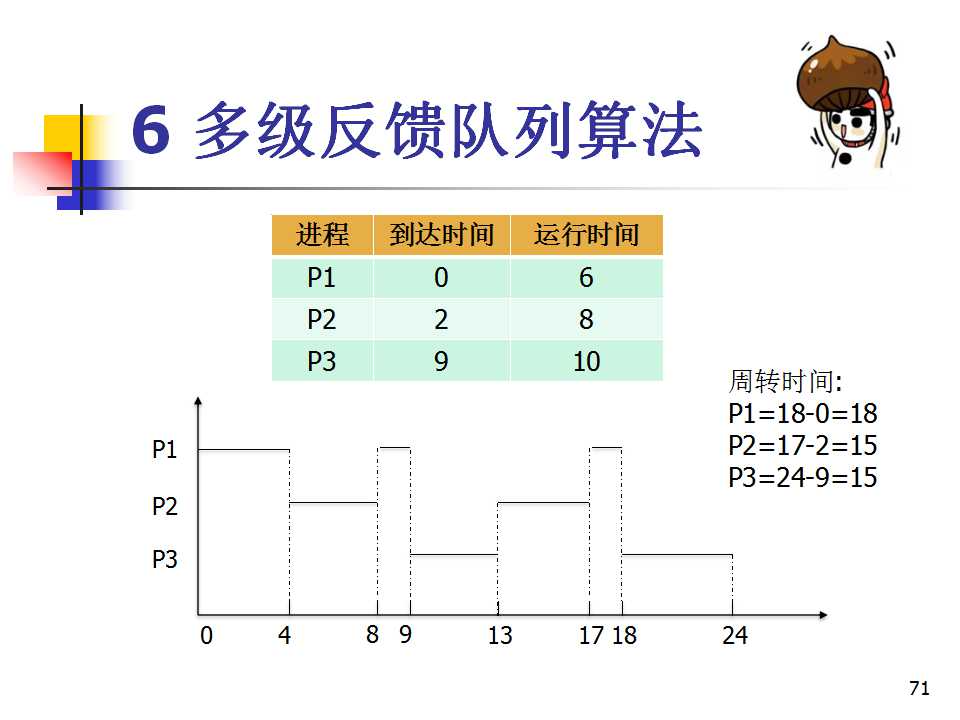
多级反馈队列调度算法如下原理：

  • 1、设有N个队列（Q1,Q2…QN），其中各个队列对于处理机的优先级是不一样的，也就是说位于各个队列中的作业(进程)的优先级也是不一样的。一般来说，优先级Priority(Q1) > Priority(Q2) > … > Priority(QN)。怎么讲，位于Q1中的任何一个作业(进程)都要比Q2中的任何一个作业(进程)相对于CPU的优先级要高（也就是说，Q1中的作业一定要比Q2中的作业先被处理机调度），依次类推其它的队列。
  • 2、对于优先级最低的队列来说，里面是遵循时间片轮转法。也就是说，位于队列QN中有M个作业，它们的运行时间是通过QN这个队列所设定的时间片来确定的；对于其他队列，遵循的是先来先服务算法，每一进程分配一定的时间片，若时间片运行完时进程未结束，则进入下一优先级队列的末尾。
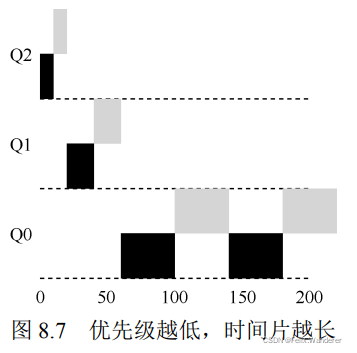
  • 3、各个队列的时间片是一样的吗？
    不一样，这就是该算法设计的精妙之处。各个队列的时间片是随着优先级的增加而减少的，也就是说，优先级越高的队列中它的时间片就越短。同时，为了便于那些超大作业的完成，最后一个队列QN(优先级最低的队列)的时间片一般很大(不需要考虑这个问题)。

上述程序在某一进程在一级队列运行一轮后没有运行完毕，若加入二级队列而不是加入原队列的尾部，则可以实现简单的多级反馈队列调度算法
两种算法的不同之处就在于：当一个RQ1中的进程在时间片结束之后是回到当前的队尾还是到RQ2队列之中。
在上述程序中也很容易实现：

		if (fin)Current->turn += clock, Fin_Insert(*Current);//运行结束    elseQ1_Insert(*Current);//进入队尾等待运行

修改为：

		if (fin)Fin_Insert(*Current);//运行结束    elseQ2_Insert(*Current);//进入二级队列等待运行Current->turn += clock,

上述两种代码分别实现了上述两种功能，执行时只需选一种在相应位置即可。

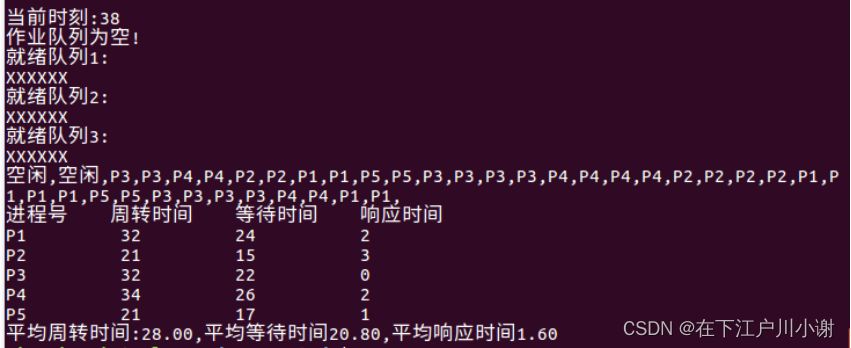
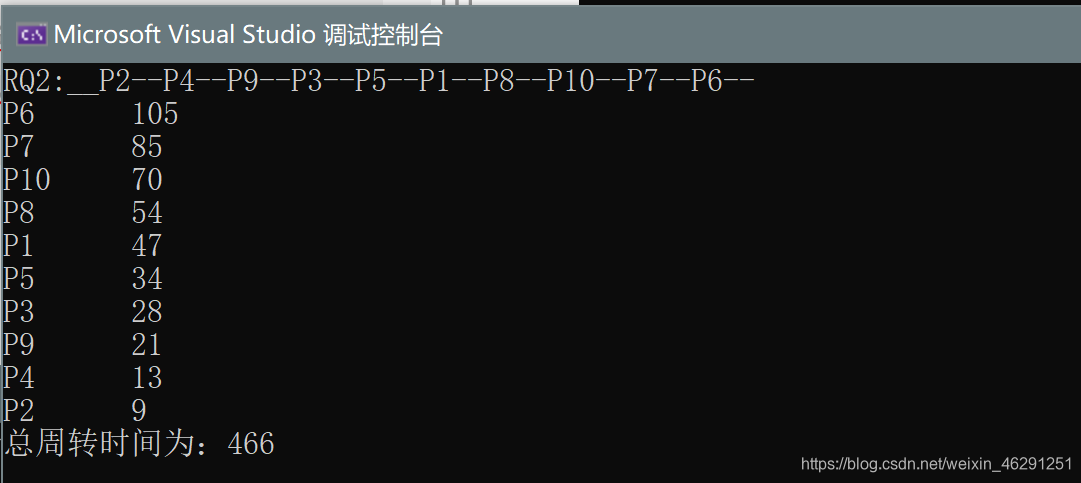
  • 多级反馈队列调度测试结果：在这里插入图片描述

由分析上述数据容易发现：在该测试数据的情况下多级反馈队列调度算法是要优于多级队列调度的


http://chatgpt.dhexx.cn/article/2JmUeyUe.shtml

相关文章

多级反馈队列调度算法模拟实现

多级反馈队列调度算法模拟实现

实验一 多级反馈队列调度算法 一. 主要实现方法和代码介绍 ​ 1.编写进程类,其只包含所需的运行时间和进程编号两个属性,还有一个运行方法,此方法就是将所需的运行时间属性减去.传入的运行时间. ​ 2.创建进程函数:创建maxp个进程,(应该不超过10,在此创建九个,即暂时不进行进…
阅读更多...
计操实验 多级反馈队列C语言

计操实验 多级反馈队列C语言

计操实验 多级反馈队列C语言 需求&#xff1a; 1.队列4级&#xff0c;每一级的队列长度均为10&#xff1b;第一级的时间片为T&#xff0c;第二级的时间片为2T&#xff0c;第三级的时间片为4T&#xff0c;第四级的时间片为8T&#xff1b;&#xff08;T的大小自己定&#xff09; …
阅读更多...
【操作系统】轮转和多级反馈队列

【操作系统】轮转和多级反馈队列

随着计算机的技术逐渐步入家用后&#xff0c;新的调度指标接踵而来&#xff0c;周转时间已经不能满足人们日常工作的需求&#xff0c;更多时候人们更希望计算机能有更好的交互性&#xff0c;使其能更快地去响应任务&#xff0c;由此针对优化响应时间的调度策略也遍地开花&#…
阅读更多...
多级反馈队列调度算法(c++)

多级反馈队列调度算法(c++)

如果对你有帮助&#xff0c;可以给卑微的博主留个赞、关注、收藏 (不是) (骗一下数据&#xff0c;说不定以后面试就过了&#xff0c;拜谢) 操作系统基本调度算法&#xff0c;多级反馈队列调度算法。在划分时间片的调度算法中&#xff0c;多级反馈队列算法兼顾提高系统吞吐…
阅读更多...
多级反馈队列调度算法

多级反馈队列调度算法

实验目的&#xff1a; 在Linux下编程实现多级反馈队列调度算法&#xff0c;采用三级调度策略&#xff0c;所有进程先按到达顺序进入一级队列&#xff0c;按照时间片为2轮转一次&#xff0c;一个时间片内未完成的进程被依次移入二队列尾部。当一级队列中没有进程时&#xff0c;开…
阅读更多...
多级反馈队列调度

多级反馈队列调度

多级反馈队列 ​ 多级反馈队列&#xff08;Multi-level Feedback Queue&#xff0c; MLFQ&#xff09;&#xff0c;与上个世纪70年代提出&#xff0c;主要应用于时分共享系统。主要解决两方面问题&#xff1a;一个是优化周转时间&#xff0c;一个是要给用户很好的交互体验。ML…
阅读更多...
多级反馈队列算法

多级反馈队列算法

步骤&#xff1a; 0时刻&#xff0c;P1到达就绪队列&#xff08;时间片为4的&#xff09;P1先执行2ms&#xff0c;P2到达还未到时间片&#xff0c;P1继续执行2ms后&#xff0c;时间片到达了&#xff0c;P1滑到下一个就绪队列&#xff08;时间片为6的&#xff09;此时&#xff…
阅读更多...
linux多级反馈队列的实现,多级反馈队列调度算法详解

linux多级反馈队列的实现,多级反馈队列调度算法详解

通常在使用多级队列调度算法时&#xff0c;进程进入系统时被永久地分配到某个队列。例如&#xff0c;如果前台和后台进程分别具有单独队列&#xff0c;那么进程并不从一个队列移到另一个队列&#xff0c;这是因为进程不会改变前台或后台的性质。这种设置的优点是调度开销低&…
阅读更多...
对数线性模型

对数线性模型

http://blog.csdn.net/pipisorry/article/details/52788947 特征和指示特征 对数线性模型log linear model 对数线性模型有&#xff1a;最大熵模型和逻辑斯谛回归。 [概率图模型原理与技术] [PGM&#xff1a;无向图模型&#xff1a;马尔可夫网 ] 皮皮blog 最大熵模型的一般形式…
阅读更多...
广义线性模型（Generalized Linear Model）之三：Poisson回归

广义线性模型（Generalized Linear Model）之三：Poisson回归

广义线性模型&#xff08;Generalized Linear Model&#xff09;之三&#xff1a;Poisson回归 一、泊松回归&#xff08;Poisson regression&#xff09;简介&#xff08;一&#xff09;泊松回归&#xff08;二&#xff09;计数数据&#xff08;三&#xff09;泊松分布1&#x…
阅读更多...
MIT自然语言处理第五讲：最大熵和对数线性模型

MIT自然语言处理第五讲：最大熵和对数线性模型

MIT自然语言处理第五讲&#xff1a;最大熵和对数线性模型&#xff08;第一部分&#xff09; 自然语言处理&#xff1a;最大熵和对数线性模型 Natural Language Processing: Maximum Entropy and Log-linear Models 作者&#xff1a;Regina Barzilay&#xff08;MIT,EECS Depar…
阅读更多...
机器学习教程 之 线性模型：线性回归、对数几率回归、线性判别分析

机器学习教程 之 线性模型：线性回归、对数几率回归、线性判别分析

常用的三个线性模型的原理及python实现——线性回归&#xff08;Linear Regression&#xff09;、对数几率回归&#xff08;Logostic Regression&#xff09;、线性判别分析&#xff08;Linear Discriminant&#xff09;。 这可能会是对线性模型介绍最全面的博客 文章目录 一、…
阅读更多...
机器学习（二）线性模型——线性回归、对数几率回归、线性判别分析

机器学习（二）线性模型——线性回归、对数几率回归、线性判别分析

一、线性回归 线性回归&#xff08;linear regression&#xff1a;试图学得一个线性模型以尽可能准确地预测实值输出标记。 1.最简单的形式&#xff1a;输入属性的数且只有一个&#xff0c; 最小二乘法&#xff1a;基于均方差误差最小化来进行模型的求解&#xff0c;在线性回…
阅读更多...
对数线性模型：逻辑斯谛回归和最大熵模型

对数线性模型：逻辑斯谛回归和最大熵模型

http://blog.csdn.net/pipisorry/article/details/52788947 对数线性模型log linear model 对数线性模型有&#xff1a;最大熵模型和逻辑斯谛回归。 特征和指示特征 对数线性模型的一般形式 [概率图模型原理与技术] 某小皮 对数线性模型的不同形式 因子图 将因子转换到对…
阅读更多...
从线性到非线性模型-对数线性模型

从线性到非线性模型-对数线性模型

从线性到非线性模型 1、线性回归&#xff0c;岭回归&#xff0c;Lasso回归&#xff0c;局部加权线性回归 2、logistic回归&#xff0c;softmax回归&#xff0c;最大熵模型 3、广义线性模型 4、Fisher线性判别和线性感知机 5、三层神经网络 6、支持向量机 code: https://…
阅读更多...
论文总结3 对数线性模型 罗盛

论文总结3 对数线性模型 罗盛

研究变量之间的相互关系、列联表、对应分析 目录 一、模型介绍 二、比较-对数线性模型&对应分析 1.相同&不同 2.相互关系 三、应用实例 1.模型确立 2.列因素&因子负荷 四、总结经验 一、模型介绍 列联表分析无法系统地评价变量间的联系&#xff0c;无法…
阅读更多...
对数线性模型之一(逻辑回归), 广义线性模型学习总结

对数线性模型之一(逻辑回归), 广义线性模型学习总结

经典线性模型自变量的线性预测就是因变量的估计值。 广义线性模型：自变量的线性预测的函数是因变量的估计值。常见的广义线性模型有：probit模型、poisson模型、对数线性模型等等。对数线性模型里有：logistic regression、Maxinum entropy。本篇是对逻辑回归的学习总结，以及…
阅读更多...
机器学习篇——对数线性模型

机器学习篇——对数线性模型

建议首先看cs229讲的广义线性模型、exponential family&#xff08;指数分布族&#xff09; 对数线性模型包括逻辑回归、最大熵模型和条件随机场等 1、模型 条件概率分布&#xff08;对数线性模型、概率模型&#xff09;、判别模型 逻辑回归&#xff1a; 概率分布可由广…
阅读更多...
对数线性模型(Logistic回归算法)

对数线性模型(Logistic回归算法)

1.Logistic分布&#xff1a; logistic分布定义&#xff1a;设X是连续随机变量&#xff0c;X服从logistic分布&#xff0c;即为X具有下列分布函数和密度函数&#xff1a; 其中&#xff0c;mu为位置参数&#xff0c;r>0为形状参数&#xff1b; logistic分布的分布函数F(x)的…
阅读更多...
Log-Linear Models

Log-Linear Models

一&#xff0c;简介 引入 对数线性模型被广泛应用于NLP中&#xff0c;对数线性模型的一个关键优点在于它的灵活性&#xff1a;它允许非常丰富的特征集合被用于模型中。常见的对数线性模型有Logistic回归、最大熵模型、MEMMs和CRFs等。 目的 1&#xff0c;Trigram LM Trigr…
阅读更多...
推荐文章

Copyright @ 2022~2023