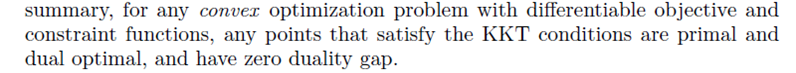【阅读时间】8min - 10mun

【内容简介】直观的解读了什么是拉格朗日乘子法，以及如何求解拉格朗日方程，并且给出几个直观的例子，针对不等式约束解读了KKT条件的必要条件和充分条件

What & Why

拉格朗日乘法(Lagrange multiplier)是一种在最优化的问题中寻找多元函数在其变量受到一个或多个条件的相等约束时的求局部极值的方法。这种方法可以将一个有 n 个变量和 k 个约束条件的最优化问题转换为一个解有 n+k 个变量的方程组的解的问题

考虑一个最优化问题

$$

\operatorname*{max}_{x,y} f(x,y) \qquad s.t.\;\; g(x,y)=c

$$

为了求 $x$ 和 $y$ ，引入一个新的变量 $\lambda$ 称为拉格朗日乘数，再引入朗格朗日函数的极值

$$

\mathcal{L}(x,y,\lambda)=f(x,y)-\lambda \cdot \bigl( g(x,y) - c\bigl) \tag 1

$$

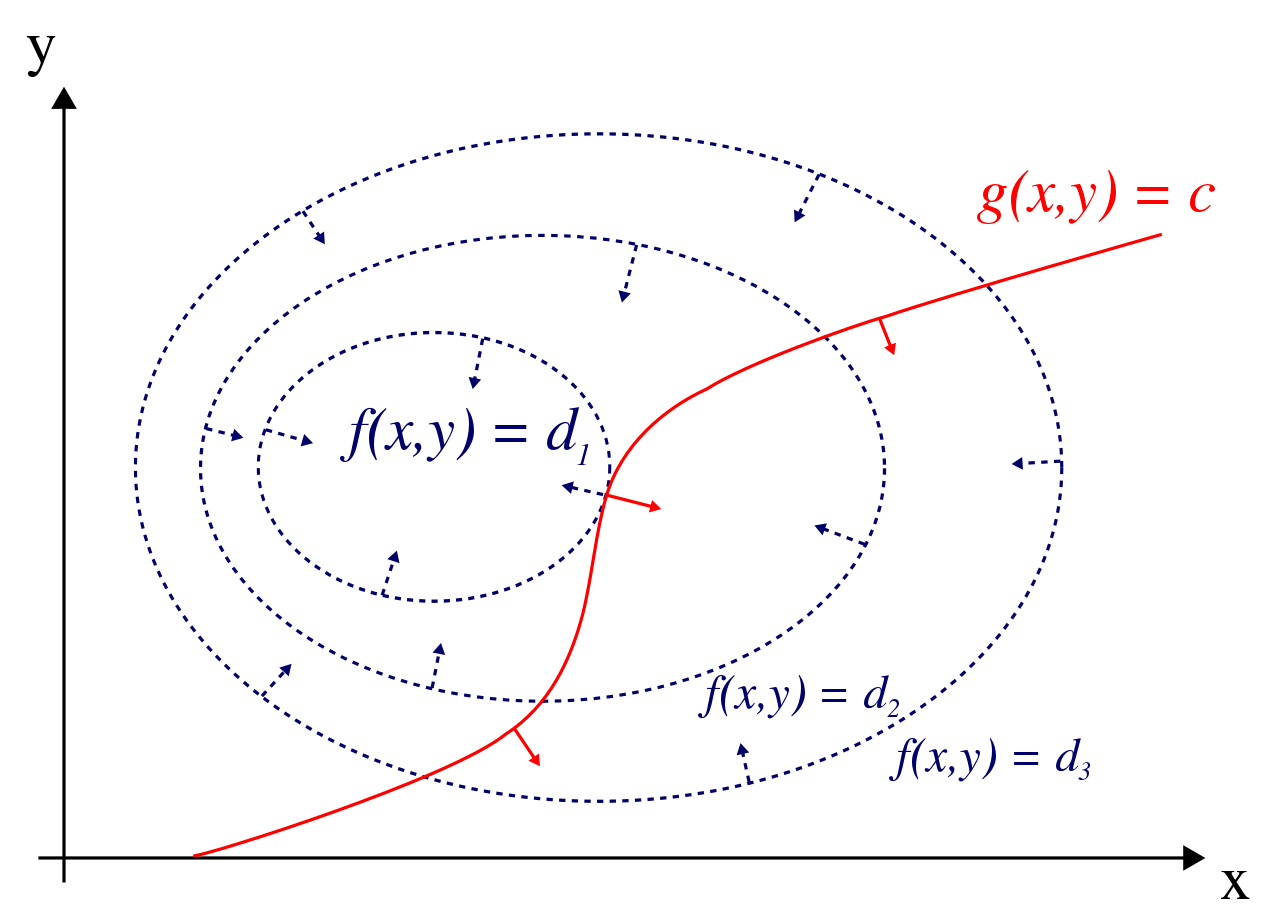
红线表示 $g(x,y) = c$ ，蓝线是 $f(x,y)$ 的等高线，所有箭头表示梯度下降最快的方向。图中红线与等高线相切的位置就是待求的极大值

How

那么如何求这个极值点呢？

单约束

对(1)式直接求微分，并令其为零，计算出鞍点