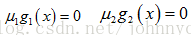主要参考这篇文章和这个知乎回答。
KKT最优化条件是Karush[1939],以及Kuhn和Tucker[1951]先后独立发表出來的。这组最优化条件在Kuhn和Tucker发表之后才逐渐受到重视,因此许多情况下只记载成库恩塔克条件(Kuhn-Tucker conditions)
它是非线性规划领域的重要成果,是判断某点是极值点的必要条件。对于凸规划,KKT条件就是充要条件了,只要满足则一定是极值点,且一定得到的是全局最优解(凸问题)。
KKT条件的引入推广了拉格朗日乘子法,拉格朗日乘数法原本只是解决等式约束下的优化问题,本科的高数里就讲了(我竟读研了才学懂,惭愧),而引入KKT条件的拉格朗日乘子法可用于更普遍的有不等式约束的情况。

(一)问题模型
“等式约束+不等式约束” 优化问题是最复杂也最常见的一种模型。问题建模为:
min f ( x ) s . t . h k ( x ) = 0 , g j ( x ) ≤ 0 j = 1 , 2 … , n ; k = 1 , 2 … , l \min f(x) \quad s.t.h_k(x)=0\quad,\quad g_j(x)\leq0\quad j=1,2\ldots,n;k=1,2\ldots,l minf(x)s.t.hk(x)=0,gj(x)≤0j=1,2…,n;k=1,2…,l
思路是要把问题转化为无约束的简单优化问题,分为两步:
- 先把不等式约束条件转化为等式约束条件。 how? → \to → 引入 松弛变量,即KKT乘子
- 再把等式约束转化为无约束优化问题。 how? → \to → 引入拉格朗日乘子
(二)一点铺垫
后面要用这个结论:
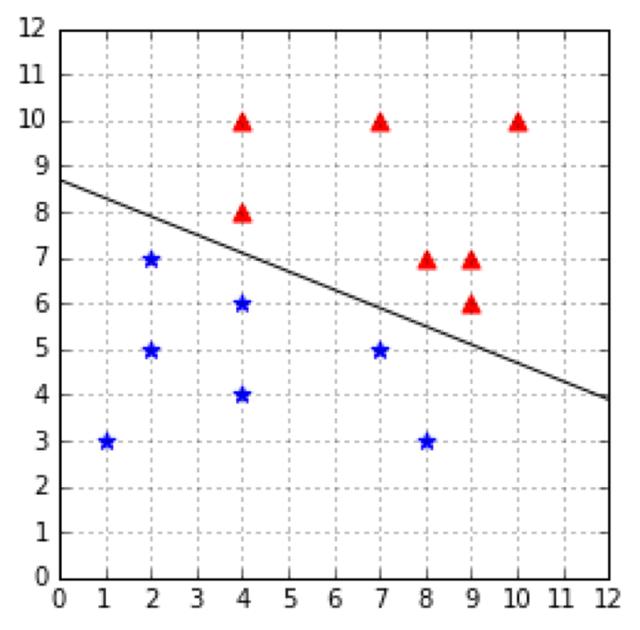
实质上,KKT条件描述的是:这个点已经是可行域(满足所有约束条件的n维空间)的边界了,再走一点就不满足约束条件了。显然,最优解一定在可行域的边界上的,以初中学的线性规划作为简单的例子,
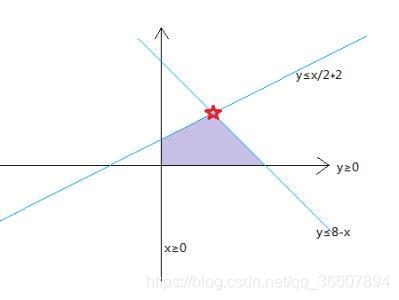
这张图的紫色区域就是四个不等式约束限定的可行域,如果求z=x+2y的最大值,结果当然是红星点取得最大值,总之极值点应该在可行域的边界,这在自变量多的高维可行域空间也是如此,只是不好画图直观去看了。
(三)KKT到底是什么
KKT条件就是说:
如果一个点 x ∗ x^* x∗是满足所有约束的极值点,那么
{ ∇ f ( x ∗ ) + ∑ k λ k ∇ h k ( x ∗ ) + ∑ j μ j ∇ g j ( x ∗ ) = 0 ( 1 ) μ j ≥ 0 ( 2 ) μ j g j ( x ∗ ) = 0 ( 3 ) g j ( x ∗ ) ≤ 0 ( 4 ) \left\{ \begin{aligned} \nabla f(x^*) + \sum_{k}\lambda_k\nabla h_k(x^*)+\sum_{j}\mu_j\nabla g_j(x^*)&=&0 \quad (1)\\ \mu_j & \geq & 0 \quad (2)\\ \mu_jg_j(x^*) & = &0\quad (3)\\ g_j(x^*) &\leq &0 \quad(4)\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∇f(x∗)+k∑λk∇hk(x∗)+j∑μj∇gj(x∗)μjμjgj(x∗)gj(x∗)=≥=≤0(1)0(2)0(3)0(4)
下面进行条件的解读:
(1) 极值点处函数的梯度是约束条件梯度的线性组合;只有满足 g j ( x ∗ ) = 0 g_j(x^*)=0 gj(x∗)=0的那些不等式约束的梯度才会出现在加权式中,才有资格给人加权。
(2) 不等式约束的权值(KKT乘子)必须大于等于0,因为f(x) 和g(x)的梯度方向必须相反。
解释如下:

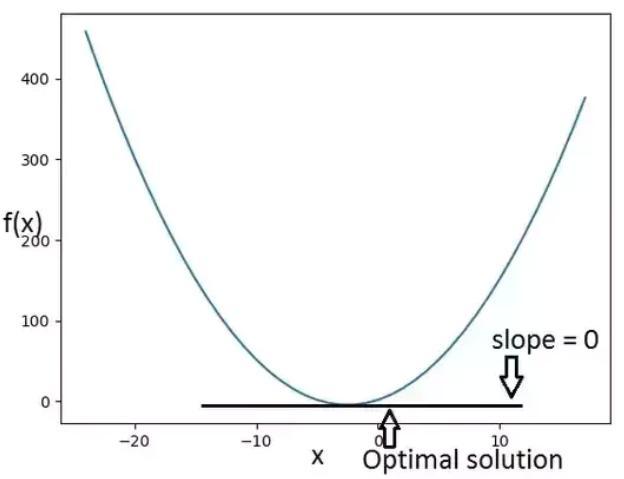
假设某问题的可行域就是(b)图画的这样,仅为便于理解哈,实际可行域不一定必须长成这样。
前面说了,极值点肯定往可行域的边界靠,肯定不会在可行域中间某处,所以边界上极值点处的函数值自然比可行域内的函数值小(这里最小化目标函数,如果是最大化,就是边界比里面大了),所以极值点处函数的梯度方向(函数值增大最快的方向)是向里面的;
而对于约束条件,可行域里的值比边界要小,所以极值点处g(x)的梯度方向朝外面!!
结了,二者必然方向相反,所以KKT乘子必然为正。
从这个推导过程你应该也能明白为啥等式约束下不要求拉格朗日乘子必须为正了。
等式约束的权值(拉格朗日乘子)的正负无要求
(3) 若某个不等式约束在极值点取值严格小于0,则这个约束条件无效,就是说有没有这个约束根本影响不了结果,其KKT乘子为0;
若极值点处不等式约束取值等于0,这个约束就是有效的,可行域的边界的构建就有它出的一份力,则其KKT乘子为正。
这也是KKT乘子为什么又被称为松弛变量的原因,因为它让 ≤ \leq ≤变成了 = = =,把不等式约束变为了等式约束,通过它的引入使得约束变得简单了。
整个可行域是由 g j ( x ) ≤ 0 g_j(x)\leq0 gj(x)≤0和 h k ( x ) = 0 h_k(x)=0 hk(x)=0围成的,但实际上有些不等式约束没对边界的形成做出贡献,就对函数在极值点处的梯度无贡献(都没在边界肯定贡献不了梯度了),所以根本不分配乘子。
总之,拉格朗日乘子法和KKT条件也算是take me a whole day了,从之前上课一直云里雾里乘飞机到现在写完博客脑子像浆糊,算是基本理清了,这篇讲KKT的文章估计读者会看的很晕,可能没完全讲清楚,但理解KKT,重点还是要从几何的角度去想,有那么点只可意会不可言传或者不太好言传的味道。我就是看一大堆博客回答受到启发(晕乎)了以后,想到极值点一定在可行域的边界,从而对三个KKT条件进行了逻辑上串得起来说得通的解读的。
数学的世界好大,我要去喘口气~~~