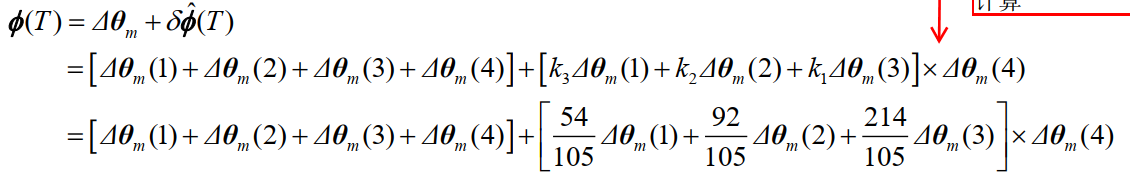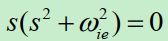1、定轴运动与非定轴运动
即转轴固定不动的转动;因此可得知,在捷联惯导应用中,X、Y、Z轴在空间中都存在转动,所以整个过程为非定轴运动。
2、不可交换性误差:
起因:在非定轴转动情况下, 描述姿态运动的微分方程是非线性的, 其离散化求解会引起转动不可交换误差。
解决:通过陀螺的输出(增量形式)构造等效旋转矢量以补偿和降低不可交换误差。
3、反对称矩阵形式
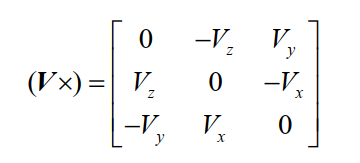
并且,反对称矩阵的转置是其负矩阵:

4、反对称矩阵的矩阵指数函数:
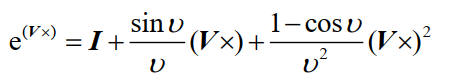
行列式为1的单位正交矩阵为右手直角坐标系变换矩阵;
行列式为-1的单位正交矩阵为左手直角坐标系变换矩阵;
5、坐标变换矩阵和坐标系变换矩阵——(注意说法)

P :从i系到b系的坐标系变换矩阵(过渡矩阵)

![]() 为从b系到i系的坐标变换矩阵;
为从b系到i系的坐标变换矩阵;
注意:前面是,坐标系变换,后面是坐标变换
关于P的特点:
(1)P 中任一行向量为单位向量, 且任意两个不同行向量之间正交
(2)由于矩阵 P 中的每一个元素均表示两套坐标系( b 系和i 系)相应坐标轴之间夹角的余弦值,因此常称 P 为方向余弦阵(direction cosine matrix, DCM)。
如果导航坐标系(以东北天为例)经过三次旋转,旋转顺序为3-1-2,得到载体坐标系;则其表达方式为:
即:0系为导航系、3系为载体坐标系(右前上);即导航系到载体系的方向余弦矩阵

6、等效旋转矢量推导:
纯数学推导:


既:结果如下:该变换是转轴u和转角Θ的函数
![]()
方向余弦矩阵和等效旋转矢量关系:

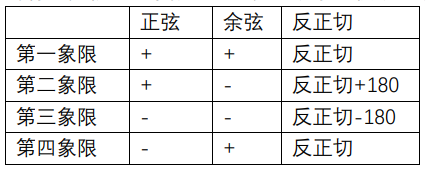
7、姿态角及轴向描述
当运载体水平停放时:
横轴沿左右方向,可取向右方向为正;
纵轴沿前后方向,可取向前方向为正;
立轴沿上下方向, 可取向上方向为正。
描述运载体的一组欧拉角通常也称为姿态角, 包括:
航向角( 方位角或偏航角,yaw/azimuth/heading)、
俯仰角(高低角或纵摇角, pitch/elevation)、
横滚角( 滚动角或横摇角,roll),各角参数的定义与运载体各物理轴向相联系,详细定义如下
以下来自《捷联惯导算法与组合导航原理讲义》附录B1
参见图 B-3:
航向角ψ : 运载体纵轴在当地水平面上的投影线与当地地理北向的夹角, 常取北偏东
为正,即若从空中俯视运载体, 地理北向顺时针旋转至纵轴水平投影线的角度, 角度范围为 0~360° ,
或[0,2π) ;俯仰角θ : 运载体纵轴与其水平投影线之间的夹角, 当运载体抬头时角度定义为正,角度范
围-90° ~90° ,或[-π/2, π/2] ;横滚角γ :运载体立轴与纵轴所在铅垂面之间的夹角,当运载体向右倾
斜时角度定义为正,角度范围-180° ~180° ,或(-π, π]。

注:如果载体坐标系为右前上,则航向角为北偏西为正!
则图 B-3 给出的运载体欧拉角定义可以简单描述为“ (-3)12”方式。 类似的, 如果oxyz(g) 和oxyz(b)分别定义为“ 北-东-地” 地理坐标系和“前-右-下” 载体坐标系, 则运载体欧拉角定义应相应地变为“ 321”方式。由此可见,实际运载体欧拉角本质上是按物理轴向定义的, 一般依次按“ 立轴下->横轴右->纵轴前” 方式进行, 而与具体数学轴向选择无关。
8、方向余弦矩阵微分方程/姿态阵微分方程:
作用:建立了动坐标系相对于参考坐标系之间方向余弦阵与动坐标系运动角速度之间的关系!

等价公式:
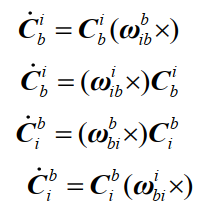
相似变换公式:
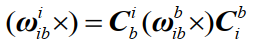
9、方向余弦阵微分方程的求解(前提是:定轴转动)
定轴转动的假设下,不存在不可交换性误差;此处只是理论分析,实际中不直接使用!
即:

经过推导,为如下:

这表示在时间段[0, ] T 内, b 系相对于 i 系的转动角速度方向始终不变, 即为定轴转动!
从数学角度上看, 转动的不可交换性在于/等价于矩阵乘法的不可交换性; 反之,姿态可交换矩阵对应于定轴转动,即若有C1C2=C2C1, 则由C1和C2 所代表的两转轴之间必定相互平行!
(1):


(2):
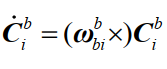
则计算结果:


10、四元数
(1)四元数乘法矩阵表示:

(2)单位四元数三角函数表示法:


(3)根据方向余弦矩阵与单位四元数(三角函数表示法),进行恒等变换:
![]()
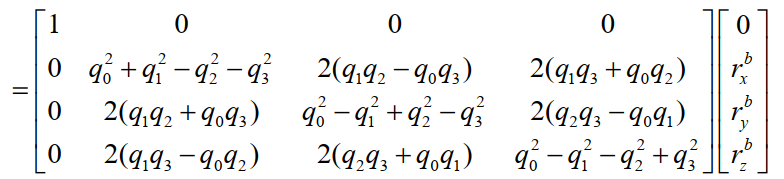
(4)利用四元数进行不同坐标系下的矢量变换

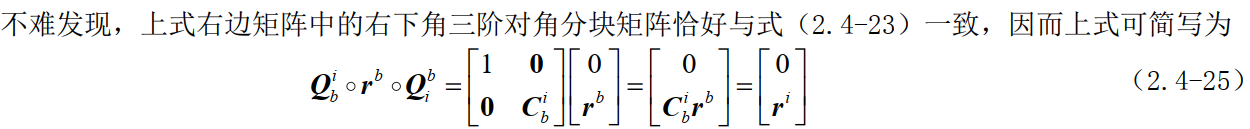
(5)四元数微分方程:
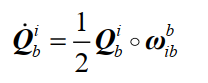
以下四种四元数微分方程之间是相互等价的:
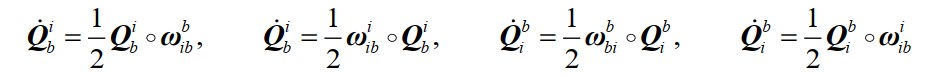
(6)四元数微分方程求解(定轴运动)


11、等效旋转矢量
(1)推导等效旋转矢量微分方程基本形式:
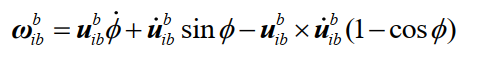
(2)等效旋转矢量微分方程:

经过简化处理,并假设在m-1时刻等效旋转矢量为0,既我们只考虑等效旋转矢量“增量”:
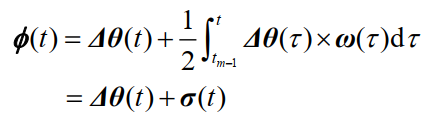

等效旋转矢量微分方程的解(泰勒展开解):以如下方程为基础推导:
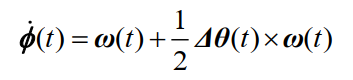
等效旋转矢量双子样:

等效旋转矢量三子样:

双子样:”前一周期+单子样“
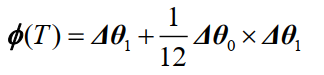
如何计算姿态?
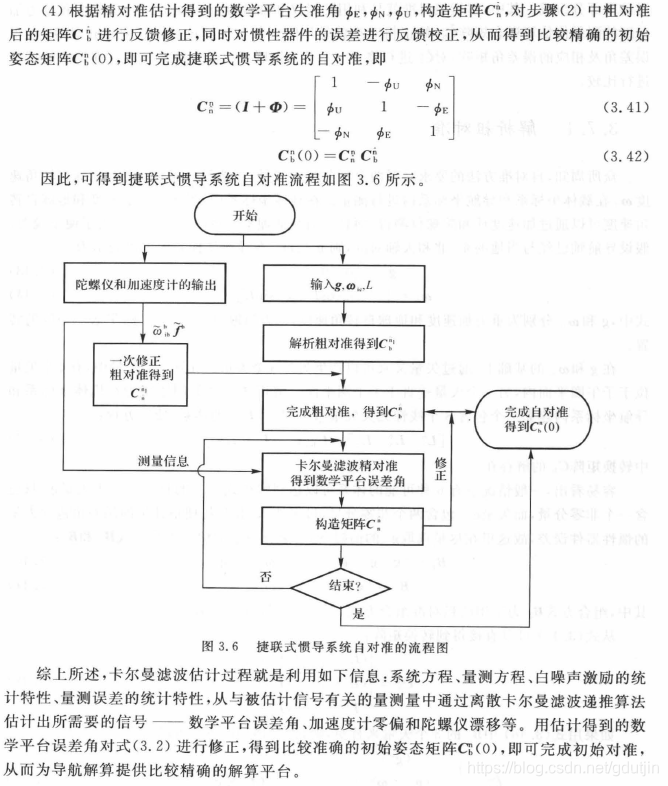
研究者们提出了先通过角增量求解等效旋转矢量(避免了不可交换性误差)、 再利用等效旋转矢量更新方向余弦阵或四元数的方法!
坐标系相对转动的四种数学描述:角速度、姿态矩阵、四元数和等效旋转矢量;
12、圆锥现象:
当陀螺仪在其旋转轴和输出轴出现同频不同相的角振动时,尽管其输入轴净指向不变(从整体上看没有随时间改变的趋势项),但陀螺仪在输入轴上还是会敏感到并输出常值角速率信号。在这种情况下,陀螺仪支架的运动角速度可描述如下:
![]()
其中, a 、 b 和c 均为常数,在 x 和 y 轴表现为同频但相位差 90° 的正弦角振动, 振动频率为Ω , 而在 z轴上表现为常值角速率。 虽然输入轴 z 轴有角速率输入,但从长时间来看陀螺仪整体上并不绕着输入轴产生明显偏转。
具体表现:
圆锥运动假设条件下:
圆锥误差补偿系数:表达式和系数表


以四字样为例: