Git使用教程
Git 是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目..
不BB了,进入正题 》
分支命名规则
- 主分支master:生产环境的稳定分支,生产环境基于该分支构建
- 开发分支develop:开发环境的稳定分支,公共开发环境基于该分支构建。
- 功能分支feature:为了开发某个特定功能,从develop分支上面分出来的,开发完成后,要merge到develop分支;功能分支的命名,可以采用feature-*的形式命名(*为版本号)
- 发布分支release: 测试环境的稳定分支,测试环境基于该分支构建
- 修复分支bug:为了修复某个bug,从release分支上面分出来的,可以采用bug-*的形式命名,修复完成后,再merge到对应的分支,修复后可以删除该分支。
git基本命令
操作步骤:
1.管理员「项目负责人」创建 git 仓库,建立 develop 分支
2.项目成员「开发者」clone 项目,在本地建立自己功能分支
3.在自己的分支上进行开发 : git add ,git commit 等,注意此时不要 push 到远程分支
4.功能完成后可直接合并本地的 develop 分支后 push 到远程仓库,合并的时候很大几率发生冲突,此时需要 merge ,merge的时候确保不影响项目其他成员,如果多个人都操作了同一个类,最好当面确认后在进行修改。等合并完成确认无误后,删除本地分支
5.管理员发布生产环境分支
并行开发bug修复流程

Eclipse git 使用教程
1.配置git
Eclipse自带git工具,我们还需要对 git 进行简单的配置。 Window->Preferences->Team->Git->Configuration,点击 Add Entry ,配置(用户邮箱和用户名)user.email 和 user.name,当提交代码时,这些信息会自动被读取提交。

2.克隆仓库
输入克隆仓库地址

下一步,修改存储路径,选择初始化分支

3.导入工程
选择仓库,import existing maven projects

导入想要的工程
4.分支管理
建议不要直接在主分支或开发分支上直接提交代码,所以整体流程是:
先新建自己的本地分支,本地分支开发完后只提交到本地,然后切换到开发分支,pull一下最新代码,把本地分支合并到开发分支,检查代码有没有冲突,没问题后push。
㈠新建分支New


㈡切换分支Switch

㈢提交分支Commit
◆流程:切换到本地分支 ->提交代码 ->切到开发分支->pull->合并本地分支->push

在local分支上开发完后提交代码(是否需要远程push视情况而定),切换到开发分支 pull一下,合并代码;
检查没问题后push



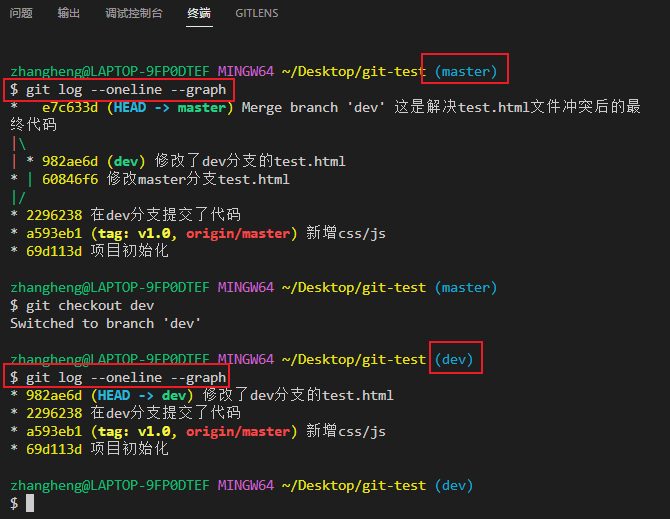
㈣合并分支Merge
当前切换到哪个分支就是要合并的目标分支,然后选中merge


㈤更新分支Pull
◆流程:切换到开发分支 ->pull ->切到本地分支->合并开发分支

更新最新代码到本地分支进行开发

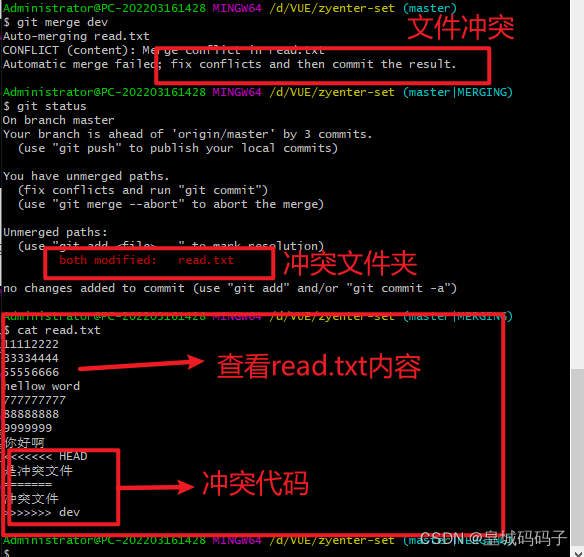
代码冲突处理
Pull 或merge操作都有可能发生冲突,需要手动处理冲突后才能提交,下面是具体解决方法:
①打开同步工具 synchronize

②用merge tool打开冲突文件

③修改代码
在自己代码区修改正确代码后 点击 Add to Index

④提交代码

⑤推送远程push