直线拟合最小二乘法

article/2025/11/8 4:54:07

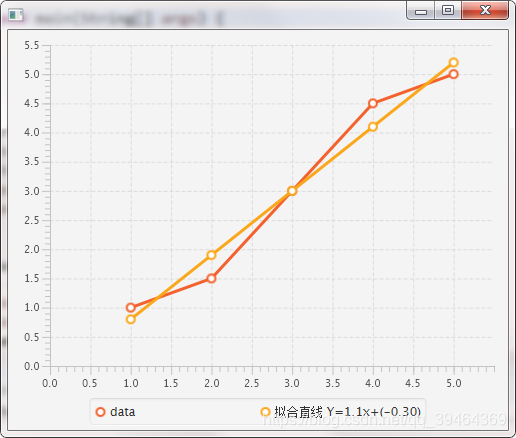
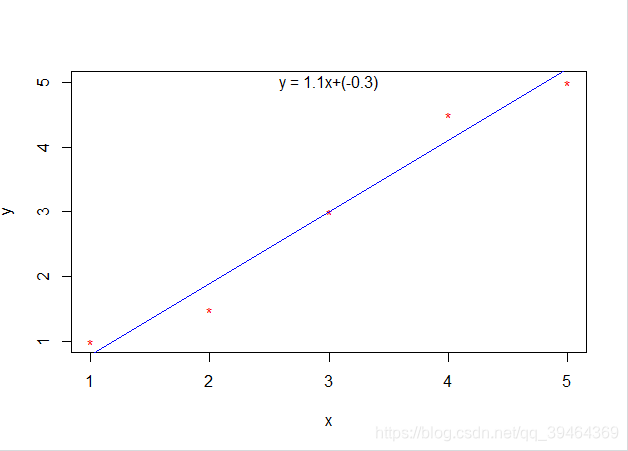
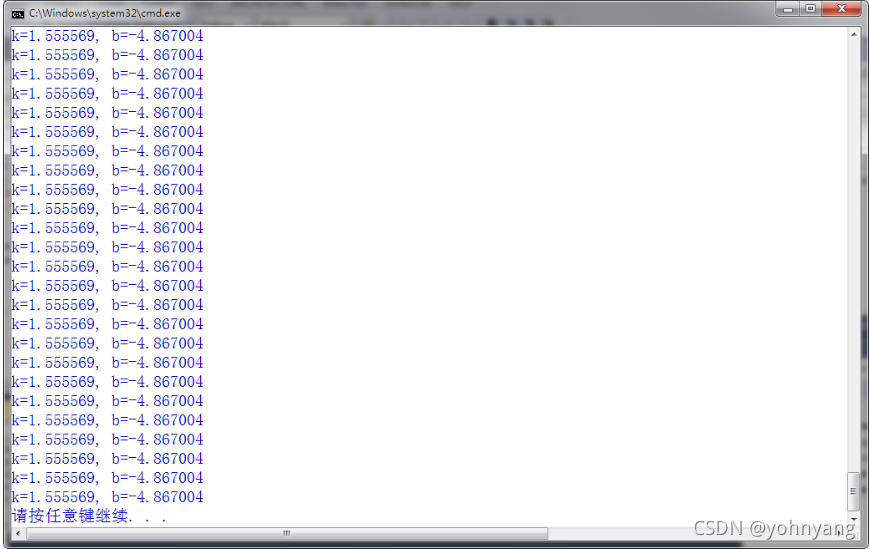
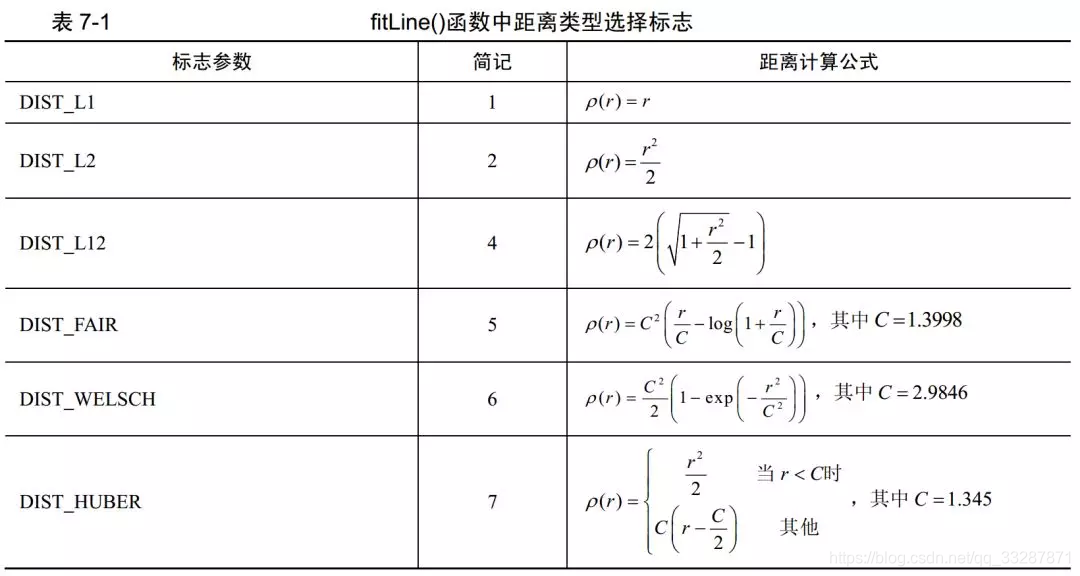
数据

x=(1,2,3,4,5)

y = (1,1.5,3,4.5,5)

算法结果

在这里插入图片描述

R语言运行结果

在这里插入图片描述

算法原理

x的均值：

xp=sum（x1+x2+x3+…+xn）/n

y的均值 :

yp=sum（y1+y2+y3+…+yn）/n

x的平方差之和：

lxx=sum( (xi-xp) ^ 2 )

协方差之和

lxy=sum( (xi-xp)*(yi-yp) )

拟合直线 y’=kx+b

k=lxy / lxx

b=yp-k*xp

代码实现

（数据容器选用集合，这样可以把数据当向量运算）

集合求和方法

	public  static double sum(List<Number> c) {try {Objects.requireNonNull(c);}catch (Exception e) {return Double.NaN;}double ret=0;Iterator<Number> itr=c.iterator();while(itr.hasNext()) {ret+=itr.next().doubleValue();}return ret;}

由于计算协方差需要集合内所有数作乘法，与求和一样，都是对连续计算每个元素，不如定义一个连续计算方法。

集合连续计算方法

第一个参数为一个集合
第二个参数为函数接口，入参1为记录值，入参2为待计算值，出参为计算后的值，是下次迭代的入参1。

	//Continuous computationpublic  static double conc(List<Number> c,BiFunction<Number,Number,Number> fun) {try {Objects.requireNonNull(c);}catch (Exception e) {return Double.NaN;}Number ret=null;Iterator<Number> itr=c.iterator();while(itr.hasNext()) {if(ret==null) {ret=itr.next();}else{ret=fun.apply(ret,itr.next().doubleValue());	//	System.out.println("");}}return ret.doubleValue();}

使用方法，（计算方法由函数接口决定）：
可以求和：
conc(x,(r,n)->r.doubleValue()+n.doubleValue());
可以求积：
conc(x,(r,n)->r.doubleValue()*n.doubleValue());

对集合内每一个元素进行计算更新

计算 xi-xp

	public static  BiFunction< List<Number>,Function<Number,Number>,List<Number> > calc=new BiFunction< List<Number>,Function<Number,Number>,List<Number> >() {public List<Number> apply(List<Number> a, Function<Number,Number> fun) {try {Objects.requireNonNull(a);Objects.requireNonNull(fun);}catch (Exception e) {return null;}List<Number> b=new ArrayList();a.forEach(itme->{b.add(fun.apply(itme));});return b;}};

多个集合运算生成新集合

主要计算协方差----两个集合相乘 (xi-xp)*(yi-yp)

	public static  BiFunction< List<List<Number>>,Function<List<Number>,Number>,List<Number> > call=new BiFunction<  List<List<Number>> ,Function<List<Number>,Number>,List<Number> >() {public List<Number> apply( List<List<Number>> c, Function<List<Number>,Number> fun) {try {Objects.requireNonNull(c);Objects.requireNonNull(fun);}catch (Exception e) {return null;}int width=c.size();List<Number> b=new ArrayList();int height=c.get(0).size();for(int h=0;h<height;h++) {List<Number> tmp=new ArrayList();for(int w=0;w<width;w++) {tmp.add(c.get(w).get(h));} b.add(fun.apply(tmp));}return b;}};

拟合算法

	public static double[] lineFit(List<Number> x,List<Number> y){double xp=mean(x);List<Number> xi_xp = calc.apply(x,e->e.doubleValue()-xp);double lxx = sum(  calc.apply(xi_xp,e->e.doubleValue()*e.doubleValue()) ); System.out.println(lxx);double yp=mean(y);List<Number> yi_yp = calc.apply(y,e->e.doubleValue()-yp);double lxy = sum( call.apply(Arrays.asList(xi_xp,yi_yp),e->conc(e,(r,n)->r.doubleValue()*n.doubleValue()) ));double k=lxy/lxx;double b=yp-k*xp;return new double[] {k,b};}

完整代码

package utility;import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Iterator;
import java.util.List;
import java.util.Objects;
import java.util.function.BiFunction;
import java.util.function.Function;import javafx.application.Application;
import javafx.scene.Parent;
import javafx.scene.Scene;
import javafx.scene.chart.LineChart;
import javafx.scene.chart.NumberAxis;
import javafx.scene.chart.XYChart.Data;
import javafx.scene.chart.XYChart.Series;
import javafx.stage.Stage;
public class LineFit extends Application{public  static double sum(List<Number> c) {try {Objects.requireNonNull(c);}catch (Exception e) {return Double.NaN;}double ret=0;Iterator<Number> itr=c.iterator();while(itr.hasNext()) {ret+=itr.next().doubleValue();}return ret;}//Continuous computationpublic  static double conc(List<Number> c,BiFunction<Number,Number,Number> fun) {try {Objects.requireNonNull(c);}catch (Exception e) {return Double.NaN;}Number ret=null;Iterator<Number> itr=c.iterator();while(itr.hasNext()) {if(ret==null) {ret=itr.next();}else{ret=fun.apply(ret,itr.next().doubleValue());	}}return ret.doubleValue();}public  static  double mean(List<Number> c) {try {Objects.requireNonNull(c);}catch (Exception e) {return Double.NaN;}double ret = c.size()>0? sum(c)/c.size():0;return ret;}public static double[] lineFit(List<Number> x,List<Number> y){double xp=mean(x);List<Number> xi_xp = calc.apply(x,e->e.doubleValue()-xp);	double lxx = sum(  calc.apply(xi_xp,e->e.doubleValue()*e.doubleValue()) ); double yp=mean(y);List<Number> yi_yp = calc.apply(y,e->e.doubleValue()-yp);double lxy = sum( call.apply(Arrays.asList(xi_xp,yi_yp),e->conc(e,(r,n)->r.doubleValue()*n.doubleValue()) ));double k=lxy/lxx;double b=yp-k*xp;return new double[] {k,b};}public static void main(String[] args) {launch();}@Overridepublic void start(Stage primaryStage) throws Exception {List<Number> x = Arrays.asList(1,2,3,4,5);List<Number> y = Arrays.asList(1,1.5,3,4.5,5);primaryStage.setScene(new Scene(plot(x,y)));primaryStage.show();}public Series<Number, Number> test(List<Number> x,List<Number> y){double[] kb = lineFit(x,y);double k = kb[0];double b = kb[1];Iterator<Number> xi = x.iterator();Series<Number, Number> series = new LineChart.Series<Number,Number>();while(xi.hasNext()) {Number tmp = xi.next();series.getData().add(new Data(tmp,k*tmp.doubleValue()+b));}series.setName("拟合直线 "+"Y="+k+"x+("+String.format("%.2f",b)+")");return series;}public  Series<Number, Number> data(List<Number> x,List<Number> y){Series<Number, Number> series = new LineChart.Series<Number,Number>();Iterator<Number> xi = x.iterator();Iterator<Number> yi = y.iterator();while(xi.hasNext()&&yi.hasNext()) {series.getData().add(new Data(xi.next(),yi.next()));}series.setName("data");return series;}public  Parent plot(List<Number> x,List<Number> y) {	NumberAxis xAxis=new NumberAxis();NumberAxis yAxis=new NumberAxis();LineChart chart = new LineChart(xAxis, yAxis);  chart.getData().add(data(x,y));chart.getData().add(test(x,y));return chart;}public static  BiFunction< List<Number>,Function<Number,Number>,List<Number> > calc=new BiFunction< List<Number>,Function<Number,Number>,List<Number> >() {public List<Number> apply(List<Number> a, Function<Number,Number> fun) {try {Objects.requireNonNull(a);Objects.requireNonNull(fun);}catch (Exception e) {return null;}List<Number> b=new ArrayList();a.forEach(itme->{b.add(fun.apply(itme));});return b;}};public static  BiFunction< List<List<Number>>,Function<List<Number>,Number>,List<Number> > call=new BiFunction<  List<List<Number>> ,Function<List<Number>,Number>,List<Number> >() {public List<Number> apply( List<List<Number>> c, Function<List<Number>,Number> fun) {try {Objects.requireNonNull(c);Objects.requireNonNull(fun);}catch (Exception e) {return null;}int width=c.size();List<Number> b=new ArrayList();int height=c.get(0).size();for(int h=0;h<height;h++) {List<Number> tmp=new ArrayList();for(int w=0;w<width;w++) {tmp.add(c.get(w).get(h));} b.add(fun.apply(tmp));}return b;}};
}

R语言代码

x=c(1,2,3,4,5)
y = c(1,1.5,3,4.5,5)
data1=data.frame(x=x,y=y) 
lm.data1<-lm(y~x,data=data1)
b<-round(lm.data1$coefficients[1],3) 
k<-round(lm.data1$coefficients[2],3)
plot(data1$x,data1$y,xlab="x",ylab = "y",col="red",pch="*") 
abline(lm.data1,col="blue") 
text(mean(data1$x),max(data1$y),paste("y = ",k,"x+(",k,")",sep = ""))

http://chatgpt.dhexx.cn/article/3l8F7lbb.shtml

相关文章

直线生成以及pcl直线拟合

直线生成以及pcl直线拟合

目录 写在前面codecompile&run result参考 写在前面 1、本文内容 pcl直线拟合&#xff0c;生成带噪声的直线并进行直线拟合的demo 2、平台 windows, pcl1.10.0 3、转载请注明出处&#xff1a; https://blog.csdn.net/qq_41102371/article/details/127147223 code line_…
阅读更多...
opencv 直线拟合

opencv 直线拟合

一、话说直线拟合 霍夫直线检测容易受到线段形状与噪声的干扰而失真&#xff0c;这个时候我们需要另辟蹊径&#xff0c;通过对图像进行二值分析&#xff0c;提取骨架&#xff0c;对骨架像素点拟合生成直线&#xff0c;这种做法在一些场景下非常有效&#xff0c;而且效果还比较…
阅读更多...
拟合算法之一 直线拟合

拟合算法之一 直线拟合

直线拟合 很早就想学习拟合了&#xff0c;经常听同事用到拟合&#xff0c;当时尚且一窍不通&#xff0c;必须快递加急紧追此处才是&#xff0c;也参考了网上大佬的一些宝贵经验&#xff0c;先将拟合方法总结如下&#xff1a; 最小二乘法 1.原理 2.举例实现 void fitline3(…
阅读更多...
直线拟合问题（Python实现）

直线拟合问题（Python实现）

程序如下&#xff1a; import matplotlib.pyplot as plt import numpy as npx_list [466, 741, 950, 1422, 1634] y_list [7.04, 4.28, 3.40, 2.54, 2.13] # x_list [0, 1, 3, 5] # y_list [1, 2, 4, 8]l_mat11 len(x_list) l_mat12 l_mat21 sum(x for x in x_list) l_…
阅读更多...
OpenCV直线拟合检测

OpenCV直线拟合检测

点击上方“小白学视觉”&#xff0c;选择加"星标"或“置顶” 重磅干货&#xff0c;第一时间送达本文转自&#xff1a;opencv学堂 OpenCV直线拟合检测 霍夫直线检测容易受到线段形状与噪声的干扰而失真&#xff0c;这个时候我们需要另辟蹊径&#xff0c;通过对图像进行…
阅读更多...
RANSAC 直线拟合

RANSAC 直线拟合

result&#xff1a; code&#xff1a; #include "stdafx.h". #include <opencv2\opencv.hpp> #include <iostream> #include <ctime>using namespace std; using namespace cv;//生成[0,1]之间符合均匀分布的数 double uniformRandom(void) {ret…
阅读更多...
OpenCV——直线拟合

OpenCV——直线拟合

相比于直线检测&#xff0c;直线拟合的最大特点是将所有数据只拟合出一条直线 void fitLine( InputArray points, OutputArray line, int distType,double param, double reps, double aeps ); points&#xff1a;输入待拟合直线的2D或者3D点集。line&#xff1a;输出描述直线…
阅读更多...
直线拟合

直线拟合

在进行直线拟合算法中&#xff0c;一直使用最小二乘法&#xff0c;使用时间长了&#xff0c;也比较熟练了&#xff0c;但是在最近一次使用中&#xff0c;最小二乘法在拟合垂直或者接近垂直的直线时&#xff0c;效果不好&#xff1b;斜率很大&#xff0c;使用稳定性不好。查阅《…
阅读更多...
Android 冷启动 热启动 测试

Android 冷启动 热启动 测试

一、应用的启动 启动方式 通常来说&#xff0c;在安卓中应用的启动方式分为两种&#xff1a;冷启动和热启动。 1、冷启动&#xff1a;当启动应用时&#xff0c;后台没有该应用的进程&#xff0c;这时系统会重新创建一个新的进程分配给该应用&#xff0c;这个启动方式就是冷启动…
阅读更多...
Spring Boot 热启动

Spring Boot 热启动

目的&#xff1a;修改类文件可以马上编译发布&#xff0c;提高了工作效率 步骤&#xff1a; 第一步&#xff1a; 修改pom.xml <!-- 热启动 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools&l…
阅读更多...
APP冷热启动专项测试

APP冷热启动专项测试

一、冷热启动的概念 冷启动&#xff1a;当启动应用时&#xff0c;后台没有该应用的进程&#xff0c;这时系统会重新创建一个新的进程分配给该应用&#xff0c;这个启动方式就是冷启动。 热启动&#xff1a;当启动应用时&#xff0c;后台已有该应用的进程&#xff08;例&#…
阅读更多...
嵌入式linux热启动和冷启动,使用keil判断ARM的冷启动和热启动的方法

嵌入式linux热启动和冷启动,使用keil判断ARM的冷启动和热启动的方法

微处理器:LPC2114 编译环境:Keil MDK V4.10 思路: 常把单片机系统的复位分为冷启动和热启动。所谓冷启动&#xff0c;也就是一般所说的上电复位&#xff0c;冷启动后片内外RAM的内容是随机的&#xff0c;通常是0x00或0xFF&#xff1b;单片机的热启动是通过外部电路给运行中的单…
阅读更多...
Android冷启动和热启动以及冷启动优化方案

Android冷启动和热启动以及冷启动优化方案

1、什么是冷启动和热启动 冷启动&#xff1a; 当启动应用时&#xff0c;后台没有该应用的进程&#xff0c;这时系统会重新创建一个新的进程分配给该应用&#xff0c;这个启动方式就是冷启动&#xff0c;也就是先实例化Application。热启动&#xff1a; 当启动应用时&#xff0…
阅读更多...
冷启动和热启动的区别android,app冷启动和热启动的区别（详解两者定义及区别）...

冷启动和热启动的区别android,app冷启动和热启动的区别（详解两者定义及区别）...

介绍一下 app 冷启动和热启动方式来实现 app 秒开的效果。那么，先来看看什么叫冷启动和热启动。 冷启动：指 app 被后台杀死后，在这个状态打开 app，这种启动方式叫做冷启动。 热启动：指 app 没有被后台杀死，仍然在后台运行，通常我们再次去打开这个 app，这种启动方式叫热…
阅读更多...
热启动和冷启动以及复位启动的小知识

热启动和冷启动以及复位启动的小知识

热启动和冷启动的区别&#xff1a; 1、重启是热启动。开机是冷启动。 2、热启动是通过开始菜单、任务管理器或者快捷键&#xff0c;重新启动计算机&#xff0c;叫热启动。冷启动是在关机状态下按POWER启动计算机&#xff0c;叫做冷启动 。 3、热启动是在计算机已经开启的状态…
阅读更多...
dimen属性报错

dimen属性报错

<TextViewandroid:id"id/tvQuote1"android:layout_width"fill_parent"android:layout_height"wrap_content"android:textColor"#FFFFFF"android:textSize"dimen/text_size" /> 发现问题是dimen属性出现错误 别的手机上…
阅读更多...
解决android:padding=“@dimen/activity_vertical_margin“＞ 标红问题

解决android:padding=“@dimen/activity_vertical_margin“＞ 标红问题

解决android:padding“dimen/activity_vertical_margin”> 标红问题 如果有这个问题&#xff0c;可以在values中新建一个dimen.xml文件 在dimen.xml里增加如下代码&#xff1a; <?xml version"1.0" encoding"utf-8"?><resources><…
阅读更多...
android:paddingTop=“@dimen/activity_horizontal_margin“报错（报红）解决方法

android:paddingTop=“@dimen/activity_horizontal_margin“报错（报红）解决方法

android:paddingTop"dimen/activity_horizontal_margin"报错&#xff08;报红&#xff09;解决方法 在app----->res----->values------>dimens.xml中添加如下代码&#xff1a; <dimen name“activity_horizontal_margin” / (后面还有一个尖括号)&#…
阅读更多...
android 手机适配之values适配dimen值

android 手机适配之values适配dimen值

android 适配屏幕的方式有很多,最方便最直接的无非就是适配values里的dimens文件值来进行适配. 张鸿洋大神已经写过一篇适配的文章,很详细 但是我在阅读的时候还是有点疑问,这个values-1920x1080到底是dp值还是手机分辨率,因为我在实际操作中发现这样一句话. 很明显可以看…
阅读更多...
Android开发——AS插件批量解决XML中的String/Color/Dimen硬编码

Android开发——AS插件批量解决XML中的String/Color/Dimen硬编码

1. 问题抛出 1.1 开发方面 对于日常开发中&#xff0c;每写一个"#333"&#xff0c;都要手动的在当前xml与colors.xml中来回切换&#xff0c;查看是否已经定义过&#xff0c;如果定义过则拿过来复用&#xff0c;如果没有就要新定义一个叫"#333"的资源名&a…
阅读更多...
推荐文章

Copyright @ 2022~2023