RANSAC 直线拟合

article/2025/11/8 5:07:34

result：

code：

#include "stdafx.h".
#include <opencv2\opencv.hpp>
#include <iostream>
#include <ctime>using namespace std;
using namespace cv;//生成[0,1]之间符合均匀分布的数
double uniformRandom(void)
{return (double)rand() / (double)RAND_MAX;
}//生成[0,1]之间符合高斯分布的数
double gaussianRandom(void)
{/* This Gaussian routine is stolen from Numerical Recipes and is theircopyright. */static int next_gaussian = 0;static double saved_gaussian_value;double fac, rsq, v1, v2;if (next_gaussian == 0) {do {v1 = 2 * uniformRandom() - 1;v2 = 2 * uniformRandom() - 1;rsq = v1*v1 + v2*v2;} while (rsq >= 1.0 || rsq == 0.0);fac = sqrt(-2 * log(rsq) / rsq);saved_gaussian_value = v1*fac;next_gaussian = 1;return v2*fac;}else {next_gaussian = 0;return saved_gaussian_value;}
}//根据点集拟合直线ax+by+c=0，res为残差
void calcLinePara(vector<Point2d> pts, double &a, double &b, double &c, double &res)
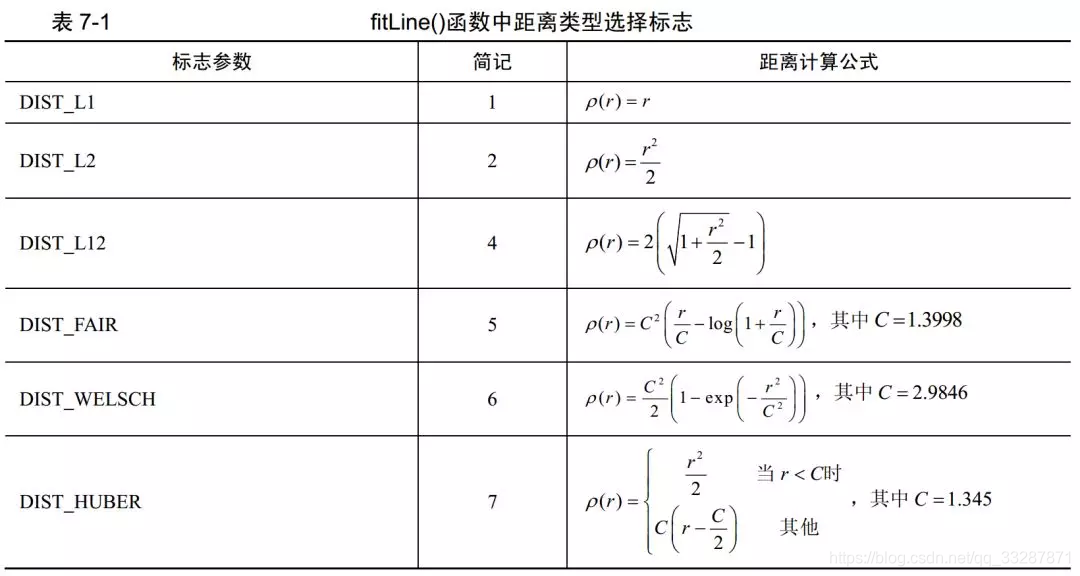
{res = 0;Vec4f line;vector<Point2f> ptsF;for (unsigned int i = 0; i < pts.size(); i++)ptsF.push_back(pts[i]);fitLine(ptsF, line, CV_DIST_L2, 0, 1e-2, 1e-2);a = line[1];b = -line[0];c = line[0] * line[3] - line[1] * line[2];for (unsigned int i = 0; i < pts.size(); i++){double resid_ = fabs(pts[i].x * a + pts[i].y * b + c);res += resid_;}res /= pts.size();
}//得到直线拟合样本，即在直线采样点集上随机选2个点
bool getSample(vector<int> set, vector<int> &sset)
{int i[2];if (set.size() > 2){do{for (int n = 0; n < 2; n++)i[n] = int(uniformRandom() * (set.size() - 1));} while (!(i[1] != i[0]));for (int n = 0; n < 2; n++){sset.push_back(i[n]);}}else{return false;}return true;
}//直线样本中两随机点位置不能太近
bool verifyComposition(const vector<Point2d> pts)
{cv::Point2d pt1 = pts[0];cv::Point2d pt2 = pts[1];if (abs(pt1.x - pt2.x) < 5 && abs(pt1.y - pt2.y) < 5)return false;return true;
}//RANSAC直线拟合
void fitLineRANSAC(vector<Point2d> ptSet, double &a, double &b, double &c, vector<bool> &inlierFlag)
{double residual_error = 2.99; //内点阈值bool stop_loop = false;int maximum = 0;  //最大内点数//最终内点标识及其残差inlierFlag = vector<bool>(ptSet.size(), false);vector<double> resids_(ptSet.size(), 3);int sample_count = 0;int N = 500;double res = 0;// RANSACsrand((unsigned int)time(NULL)); //设置随机数种子vector<int> ptsID;for (unsigned int i = 0; i < ptSet.size(); i++)ptsID.push_back(i);while (N > sample_count && !stop_loop){vector<bool> inlierstemp;vector<double> residualstemp;vector<int> ptss;int inlier_count = 0;if (!getSample(ptsID, ptss)){stop_loop = true;continue;}vector<Point2d> pt_sam;pt_sam.push_back(ptSet[ptss[0]]);pt_sam.push_back(ptSet[ptss[1]]);if (!verifyComposition(pt_sam)){++sample_count;continue;}// 计算直线方程calcLinePara(pt_sam, a, b, c, res);//内点检验for (unsigned int i = 0; i < ptSet.size(); i++){Point2d pt = ptSet[i];double resid_ = fabs(pt.x * a + pt.y * b + c);residualstemp.push_back(resid_);inlierstemp.push_back(false);if (resid_ < residual_error){++inlier_count;inlierstemp[i] = true;}}// 找到最佳拟合直线if (inlier_count >= maximum){maximum = inlier_count;resids_ = residualstemp;inlierFlag = inlierstemp;}// 更新RANSAC迭代次数，以及内点概率if (inlier_count == 0){N = 500;}else{double epsilon = 1.0 - double(inlier_count) / (double)ptSet.size(); //野值点比例double p = 0.99; //所有样本中存在1个好样本的概率double s = 2.0;N = int(log(1.0 - p) / log(1.0 - pow((1.0 - epsilon), s)));}++sample_count;}//利用所有内点重新拟合直线vector<Point2d> pset;for (unsigned int i = 0; i < ptSet.size(); i++){if (inlierFlag[i])pset.push_back(ptSet[i]);}calcLinePara(pset, a, b, c, res);
}void main()
{//demoint width = 640;int height = 320;//直线参数double a = 1, b = 2, c = -640;//随机获取直线上20个点int ninliers = 0;vector<Point2d> ptSet;srand((unsigned int)time(NULL)); //设置随机数种子while (true){double x = uniformRandom()*(width - 1);double y = -(a*x + c) / b;//加0.5高斯噪声x += gaussianRandom()*0.5;y += gaussianRandom()*0.5;if (x >= 640 && y >= 320)continue;Point2d pt(x, y);ptSet.push_back(pt);ninliers++;if (ninliers == 20)break;}int nOutliers = 0;//随机获取10个野值点while (true){double x = uniformRandom() * (width - 1);double y = uniformRandom() * (height - 1);if (fabs(a*x + b*y + c) < 10)  //野值点到直线距离不小于10个像素continue;Point2d pt(x, y);ptSet.push_back(pt);nOutliers++;if (nOutliers == 10)break;}//绘制点集中所有点Mat img(321, 641, CV_8UC3, Scalar(255, 255, 255));for (unsigned int i = 0; i < ptSet.size(); i++)circle(img, ptSet[i], 3, Scalar(255, 0, 0), 3, 8);double A, B, C;vector<bool> inliers;fitLineRANSAC(ptSet, A, B, C, inliers);B = B / A;C = C / A;A = A / A;//绘制直线Point2d ptStart, ptEnd;ptStart.x = 0;ptStart.y = -(A*ptStart.x + C) / B;ptEnd.x = -(B*ptEnd.y + C) / A;ptEnd.y = 0;line(img, ptStart, ptEnd, Scalar(0, 255, 255), 2, 8);cout << "A:" << A << " " << "B:" << B << " " << "C:" << C << " " << endl;imshow("line fitting", img);waitKey();
}

思考：

正在考虑将部分图像像素坐标点进行直线拟合，正在写这部分代码，今天只是参考原始代码，将原始代码跑通了。

I am considering fitting some image pixel coordinate points with straight line. I am writing this part of code. Today, I just refer to the original code and run through the original code.

参考：https://blog.csdn.net/YunlinWang/article/details/78147026?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.channel_param