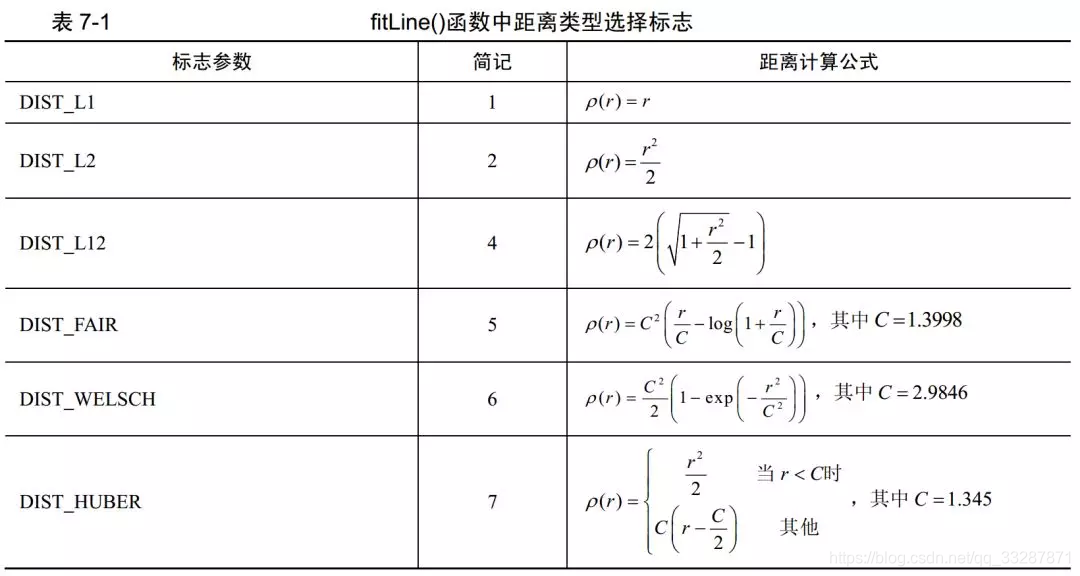
直线拟合
很早就想学习拟合了,经常听同事用到拟合,当时尚且一窍不通,必须快递加急紧追此处才是,也参考了网上大佬的一些宝贵经验,先将拟合方法总结如下:
最小二乘法
1.原理

2.举例实现
void fitline3(){float b = 0.0f, k=0.0f;vector<Point>points;points.push_back(Point(27, 39));points.push_back(Point(8, 5));points.push_back(Point(8, 9));points.push_back(Point(16, 22));points.push_back(Point(44, 71));points.push_back(Point(35, 44));points.push_back(Point(43, 57));points.push_back(Point(19, 24));points.push_back(Point(27, 39));points.push_back(Point(37, 52));Mat src = Mat::zeros(400, 400, CV_8UC3);for (int i = 0; i < points.size(); i++){//在原图上画出点circle(src, points[i], 3, Scalar(0, 255, 0), 1, 8);}int n = points.size();double xx_sum = 0;double x_sum = 0;double y_sum = 0;double xy_sum = 0;for (int i = 0; i < n; i++){x_sum += points[i].x; //x的累加和y_sum += points[i].y; //y的累加和xx_sum += points[i].x * points[i].x; //x的平方累加和xy_sum += points[i].x * points[i].y; //x,y的累加和}k = (n*xy_sum - x_sum * y_sum) / (n*xx_sum - x_sum * x_sum); //根据公式求解kb = (-x_sum * xy_sum + xx_sum*y_sum) / (n*xx_sum - x_sum * x_sum);//根据公式求解bprintf("k = %f, b = %f\n", k, b); //k = 1.555569, b = -4.867031cv::Point first = { 5, int(k * 5 + b) }, second = { int((400 - b) / k), 400 };cv::line(src, first, second, cv::Scalar(0, 0, 255), 2);cv::imshow("name", src);cv::waitKey(0);
}
上面求解出来的结果是k = 1.555569, b = -4.867031。
图像显示结果为:
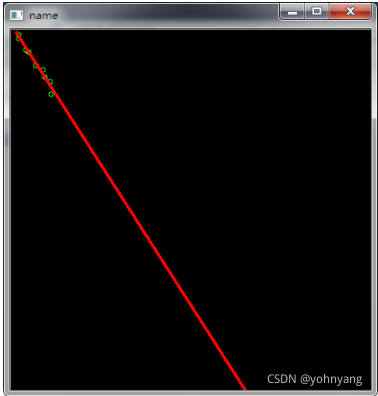
3.使用opencv自带的函数求解k和b值
void fitline1()
{vector<Point>points;//(27 39) (8 5) (8 9) (16 22) (44 71) (35 44) (43 57) (19 24) (27 39) (37 52)points.push_back(Point(27, 39));points.push_back(Point(8, 5));points.push_back(Point(8, 9));points.push_back(Point(16, 22));points.push_back(Point(44, 71));points.push_back(Point(35, 44));points.push_back(Point(43, 57));points.push_back(Point(19, 24));points.push_back(Point(27, 39));points.push_back(Point(37, 52));Mat src = Mat::zeros(400, 400, CV_8UC3);for(int i=0;i<points.size();i++){cicle(src,points[i],3,Scalar(0,0,255),1,8);}//构建A矩阵int N=2;Mat A=Mat::zeros(N,N,CV_64FC1);for (int row = 0; row < A.rows; row++){for (int col = 0; col < A.cols; col++){for (int k = 0; k < points.size(); k++){A.at<double>(row, col) = A.at<double>(row, col) + pow(points[k].x, row + col);}}}
//构建B矩阵Mat B = Mat::zeros(N, 1, CV_64FC1);for (int row = 0; row < B.rows; row++){for (int k = 0; k < points.size(); k++){B.at<double>(row, 0) = B.at<double>(row, 0) + pow(points[k].x, row)*points[k].y;}}//A*X=BMat X;//cout << A << endl << B << endl;solve(A, B, X, DECOMP_LU);cout << X << endl;vector<Point>lines;for (int x = 0; x < src.size().width; x++){ // y = b + ax;double y = X.at<double>(0, 0) + X.at<double>(1, 0)*x; //b = -4.867031, k = 1.555569,printf("b = %f, k = %f, (%d,%lf)\n", X.at<double>(0, 0), X.at<double>(1, 0), x, y);lines.push_back(Point(x, y));}polylines(src, lines, false, Scalar(255, 0, 0), 1, 8);imshow("src", src);//imshow("src", A);waitKey(0);
}梯度下降法
1.原理

2.举例实现
//梯度下降法进行线性拟合
// y = theta0 * x + theta1
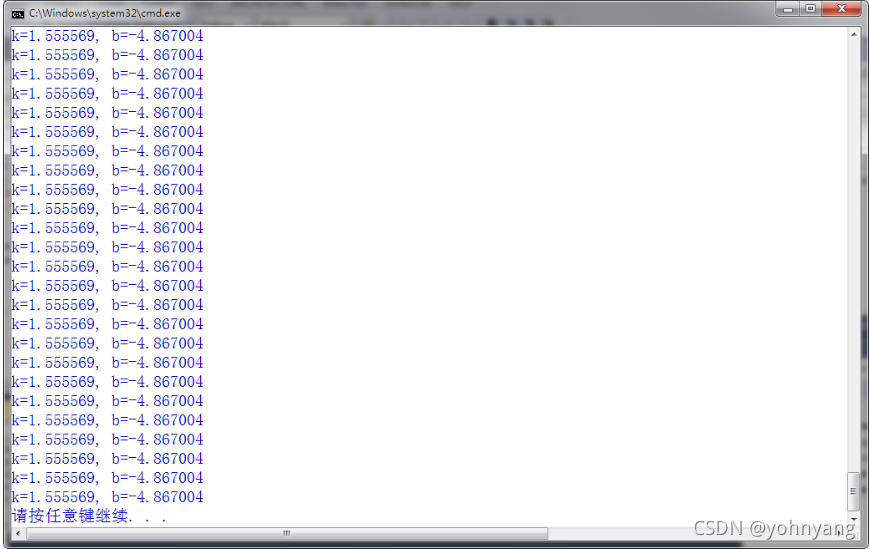
void fitline4(){const int m = 10;double Train_set_x[m] = { 27, 8, 8, 16, 44, 35, 43, 19, 27, 37 };double Train_set_y[m] = { 39, 5, 9, 22, 71, 44, 57, 24, 39, 52 };//alpha是学习率,error是结束误差,theta0就是k,theta1就是b。double theta0 = 0.0, theta1 = 0.0, alpha = 0.002, error = 1e-8; double tmp_theta0 = theta0, tmp_theta1 = theta1;double sum_theta0 = 0.0, sum_theta1 = 0.0;while (1){sum_theta0 = 0.0, sum_theta1 = 0.0;for (size_t i = 0; i < m; i++) {sum_theta0 += (theta0 * Train_set_x[i] + theta1 - Train_set_y[i])*Train_set_x[i]; sum_theta1 += (theta0 * Train_set_x[i] + theta1 - Train_set_y[i]); //累加和}theta0 = theta0 - alpha * (1.0 / m) * sum_theta0; //k更新公式theta1 = theta1 - alpha * (1.0 / m) * sum_theta1; //b更新公式printf("k=%lf, b=%lf\n", theta0, theta1);if (abs(theta0 - tmp_theta0) < error && abs(theta1 - tmp_theta1) < error){ //break;}tmp_theta0 = theta0;tmp_theta1 = theta1;}
}
结果:
参考:
1.https://blog.csdn.net/stf1065716904/article/details/107594710
2.https://blog.csdn.net/LaplaceSmoothing/article/details/94581854?utm_medium=distribute.pc_relevant.none-task-blog-2defaultCTRLISTdefault-2.no_search_link&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2defaultCTRLISTdefault-2.no_search_link