文章目录
- PT@经典二维分布@二维均匀分布@二维正态分布
- 二维均匀分布
- 性质
- 例
- 正态分布小结
- 一维正态分布
- 二维正态分布
- 二维正态分布
- 二维正态概率密度
- 边缘密度函数😊
- 分布函数😊
- 性质
- 独立性
- 二维随机变量函数的相关分布规律
- 确定性和不确定性
- 🎈正态分布的可加性
PT@经典二维分布@二维均匀分布@二维正态分布
二维均匀分布
-
设 D 为平面有界区域 , 其面积为 S D 设D为平面有界区域,其面积为S_D 设D为平面有界区域,其面积为SD
-
如果二维随机变量 ( X , Y ) 的概率密度为 : 如果二维随机变量(X,Y)的概率密度为: 如果二维随机变量(X,Y)的概率密度为:
-
f ( x , y ) = { 1 S D , ( x , y ) ∈ D 0 , e l s e f(x,y)=\begin{cases} \frac{1}{S_D},&(x,y)\in{D} \\0,&else \end{cases} f(x,y)={SD1,0,(x,y)∈Delse
-
称 ( X , Y ) 服从区域 D 上的二维均匀分布 ( X , Y ) ∼ U D ( D ) 称(X,Y)服从区域D上的二维均匀分布(X,Y)\sim{U_D(D)} 称(X,Y)服从区域D上的二维均匀分布(X,Y)∼UD(D)
-
性质
-
对于D 的子区域 , G ⊂ D 的子区域,G\sub{D} 的子区域,G⊂D
- P { ( X , Y ) ∈ G } = ∬ G f ( x , y ) d x d y = ∬ G 1 S D d x d y = 1 S D ∬ G d x d y = S G S D P\set{(X,Y)\in G}=\iint\limits_{G}f(x,y)\mathrm{d}x\mathrm{d}y =\iint\limits_{G}\frac{1}{S_D}\mathrm{d}x\mathrm{d}y =\frac{1}{S_D}\iint\limits_{G}\mathrm{d}x\mathrm{d}y =\frac{S_G}{S_D} P{(X,Y)∈G}=G∬f(x,y)dxdy=G∬SD1dxdy=SD1G∬dxdy=SDSG
-
可见, ( X , Y ) 落在 D 中的任意一个子区域 G 中的概率和 G 的面积成正比 ( 与形状 , 位置都无关 ) (X,Y)落在D中的任意一个子区域G中的概率和G的面积成正比(与形状,位置都无关) (X,Y)落在D中的任意一个子区域G中的概率和G的面积成正比(与形状,位置都无关)
- 服从平面区域上的均匀分布的二维随机变量在该区域内的取值是等可能的
例
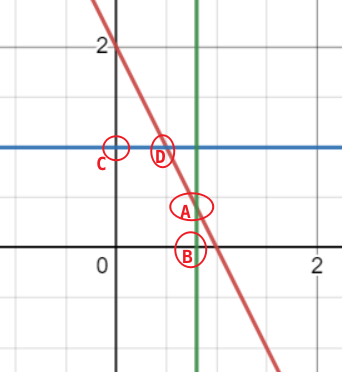
- 设 ( X , Y ) 服从区域 D 上的均匀分布 区域 D : x = 0 , y = 0 , 2 x + y = 2 所围成的面积 设(X,Y)服从区域D上的均匀分布 \\区域D:x=0,y=0,2x+y=2所围成的面积 设(X,Y)服从区域D上的均匀分布区域D:x=0,y=0,2x+y=2所围成的面积
容易得到 f ( x , y ) = { 1 , ( x , y ) ∈ D 0 , e l s e 容易得到f(x,y)= \begin{cases} 1,&(x,y)\in{D} \\0,&else \end{cases} 容易得到f(x,y)={1,0,(x,y)∈Delse
-
由 2 x + y = 2 由2x+y=2 由2x+y=2
- y = 2 − 2 x y=2-2x y=2−2x
- x = 2 − y 2 x=\frac{2-y}{2} x=22−y
-
A ( x 0 , 2 − 2 x 0 ) A(x_0,2-2x_0) A(x0,2−2x0)
-
B ( x 0 , 0 ) B(x_0,0) B(x0,0)
-
C ( 0 , y 1 ) C(0,y_1) C(0,y1)
-
D ( 2 − y 1 2 , y 1 ) D(\frac{2-y_1}{2},y_1) D(22−y1,y1)
-
从区域 D 可以看出 , f ( x , y ) 在 x ∉ [ 0 , 1 ] 内为 0 当 x ∈ [ 0 , 1 ] 时 , f ( x , y ) = 1 ; f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y = 0 + ∫ 0 2 − 2 x 1 d y + 0 = y ∣ 0 2 − 2 x = 2 − 2 x 从区域D可以看出,f(x,y)在x\notin[0,1]内为0 \\当x\in[0,1]时,f(x,y)=1; \\ f_X(x)=\int_{-\infin}^{+\infin}f(x,y)dy =0+\int_{0}^{2-2x}1dy+0=y|_{0}^{2-2x}=2-2x 从区域D可以看出,f(x,y)在x∈/[0,1]内为0当x∈[0,1]时,f(x,y)=1;fX(x)=∫−∞+∞f(x,y)dy=0+∫02−2x1dy+0=y∣02−2x=2−2x
-
从区域 D 可以看出 , f ( x , y ) 在 y ∉ [ 0 , 2 ] 内为 0 当 x ∈ [ 0 , 2 ] 时 , f ( x , y ) = 1 ; f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d x = 0 + ∫ 0 2 − y 2 1 d y + 0 = x ∣ 0 2 − y 2 = 2 − y 2 从区域D可以看出,f(x,y)在y\notin[0,2]内为0 \\当x\in[0,2]时,f(x,y)=1; \\ f_X(x)=\int_{-\infin}^{+\infin}f(x,y)dx =0+\int_{0}^{\frac{2-y}{2}}1dy+0 =x|_{0}^{\frac{2-y}{2}}=\frac{2-y}{2} 从区域D可以看出,f(x,y)在y∈/[0,2]内为0当x∈[0,2]时,f(x,y)=1;fX(x)=∫−∞+∞f(x,y)dx=0+∫022−y1dy+0=x∣022−y=22−y
正态分布小结
一维正态分布
-
仅讨论密度函数
-
一般式:
-
X ∼ ( μ , σ 2 ) X\sim(\mu,\sigma^2) X∼(μ,σ2)
-
f ( x ) = 1 2 π ⋅ σ e − 1 2 1 σ 2 ( x − u ) 2 f(x)=\frac{1}{\sqrt{2\pi}\cdot{\sigma}}e^{-\frac{1}{2}\frac{1}{\sigma^2}(x-u)^2} f(x)=2π⋅σ1e−21σ21(x−u)2
-
-
标准式
-
X ∼ ( 0 , 1 ) X\sim(0,1) X∼(0,1)
- ( μ = 0 , σ 2 = 1 \mu=0,\sigma^2=1 μ=0,σ2=1)
-
ϕ ( x ) = 1 2 π e − 1 2 x 2 \phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2} ϕ(x)=2π1e−21x2
-
二维正态分布
-
( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) (X,Y)\sim{N(\mu_1,\mu_2,\sigma_1^2,\sigma^2_2,\rho)} (X,Y)∼N(μ1,μ2,σ12,σ22,ρ)
- f ( x , y ) = 1 2 π σ 1 σ 2 1 − ρ 2 e − 1 2 ( 1 − ρ 2 ) ( ( x − μ 1 σ 1 ) 2 − 2 ρ x − μ 1 σ 1 ⋅ y − μ 2 σ 2 + ( y − μ 2 σ 2 ) 2 ) f(x,y) =\frac{1}{{2\pi}\sigma_1\sigma_2\sqrt{1-\rho^2}} \Huge e^{ \large -\frac{1}{2(1-\rho^2)} \left( (\frac{x-\mu_1}{\sigma_1})^2 -2\rho\frac{x-\mu_1}{\sigma_1}\cdot \frac{y-\mu_2}{\sigma_2} +(\frac{y-\mu_2}{\sigma_2})^2 \right) } f(x,y)=2πσ1σ21−ρ21e−2(1−ρ2)1((σ1x−μ1)2−2ρσ1x−μ1⋅σ2y−μ2+(σ2y−μ2)2)
二维正态分布
二维正态概率密度
-
设二维随机变量 ( X , Y ) 的概率密度为 : 设二维随机变量(X,Y)的概率密度为: 设二维随机变量(X,Y)的概率密度为:
-
比较和一维正态分布的密度函数的区别
- 分母: 2 π → 2 π \sqrt{2\pi}\to{2\pi} 2π→2π
- 引入参数 ρ 引入参数\rho 引入参数ρ
- 形如 : ( x − μ 1 σ 1 − y − μ 2 σ 2 ) 2 形如:(\frac{x-\mu_1}{\sigma_1}-\frac{y-\mu_2}{\sigma_2})^2 形如:(σ1x−μ1−σ2y−μ2)2
- 展开后再为混合积乘以一个 ρ \rho ρ
-
f ( x , y ) = 1 2 π σ 1 σ 2 1 − ρ 2 e − 1 2 ( 1 − ρ 2 ) ( ( x − μ 1 σ 1 ) 2 − 2 ρ x − μ 1 σ 1 ⋅ y − μ 2 σ 2 + ( y − μ 2 σ 2 ) 2 ) f(x,y) =\frac{1}{{2\pi}\sigma_1\sigma_2\sqrt{1-\rho^2}} \Huge e^{ \large -\frac{1}{2(1-\rho^2)} \left( (\frac{x-\mu_1}{\sigma_1})^2 -2\rho\frac{x-\mu_1}{\sigma_1}\cdot \frac{y-\mu_2}{\sigma_2} +(\frac{y-\mu_2}{\sigma_2})^2 \right) } f(x,y)=2πσ1σ21−ρ21e−2(1−ρ2)1((σ1x−μ1)2−2ρσ1x−μ1⋅σ2y−μ2+(σ2y−μ2)2)
-
exp
-
约定写法: exp ( f ( x ) ) = e f ( x ) \exp(f(x))=e^{f(x)} exp(f(x))=ef(x)
f ( x , y ) = 1 2 π σ 1 σ 2 1 − ρ 2 exp ( − 1 2 ( 1 − ρ 2 ) ( ( x − μ 1 σ 1 ) 2 − 2 ρ x − μ 1 σ 1 ⋅ y − μ 2 σ 2 + ( y − μ 2 σ 2 ) 2 ) ) f(x,y) =\scriptsize\frac{1}{{2\pi}\sigma_1\sigma_2\sqrt{1-\rho^2}} \exp{\left( -\frac{1}{2(1-\rho^2)} \left( (\frac{x-\mu_1}{\sigma_1})^2 -2\rho\frac{x-\mu_1}{\sigma_1}\cdot \frac{y-\mu_2}{\sigma_2} +(\frac{y-\mu_2}{\sigma_2})^2 \right) \right)} f(x,y)=2πσ1σ21−ρ21exp(−2(1−ρ2)1((σ1x−μ1)2−2ρσ1x−μ1⋅σ2y−μ2+(σ2y−μ2)2))
-
-
令 : u = u ( x ) = x − μ 1 σ 1 ; v = v ( y ) = y − μ 2 σ 2 τ = 1 − ρ 2 t = − 1 2 1 τ 2 = − 1 2 1 ( 1 − ρ 2 ) f ( x , y ) = 1 2 π σ 1 σ 2 τ exp ( t ( u 2 − 2 ρ u v + v 2 ) ) = 1 2 π σ 1 σ 2 τ exp ( − 1 2 ( 1 τ 2 ) ( u 2 − 2 ρ u v + v 2 ) ) 令: \\ u=u(x)=\frac{x-\mu_1}{\sigma_1}; \\ v=v(y)=\frac{y-\mu_2}{\sigma_2} \\ \tau=\sqrt{1-\rho^2} \\ t=-\frac{1}{2}\frac{1}{\tau^2}={-\frac{1}{2}\frac{1}{(1-\rho^2)}} \\\\ f(x,y)=\frac{1}{2\pi{\sigma_1\sigma_2}\tau}\exp{(t(u^2-2\rho{uv}+v^2))} \\=\frac{1}{2\pi{\sigma_1\sigma_2}\tau}\exp{(-\frac{1}{2}{(\frac{1}{\tau^2})}(u^2-2\rho{uv}+v^2))} 令:u=u(x)=σ1x−μ1;v=v(y)=σ2y−μ2τ=1−ρ2t=−21τ21=−21(1−ρ2)1f(x,y)=2πσ1σ2τ1exp(t(u2−2ρuv+v2))=2πσ1σ2τ1exp(−21(τ21)(u2−2ρuv+v2))
-
记为 : ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) 记为:(X,Y)\sim{N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)} 记为:(X,Y)∼N(μ1,μ2,σ12,σ22,ρ)
- μ 1 , μ 2 > 0 − 1 < ρ < 1 \mu_1,\mu_2>0\\-1<\rho<1 μ1,μ2>0−1<ρ<1
-
边缘密度函数😊
-
f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y = 1 2 π σ 1 σ 2 1 − ρ 2 ∫ − ∞ + ∞ e t ( u 2 + 2 ρ u v + v 2 ) d y = d v = 1 σ 2 d y = 1 2 π σ 1 1 − ρ 2 ∫ − ∞ + ∞ e t ( u 2 + 2 ρ u v + v 2 ) d v f_X(x)=\int_{-\infin}^{+\infin}f(x,y)\mathrm{d}y \\=\frac{1}{{2\pi}\sigma_1\sigma_2\sqrt{1-\rho^2}} \int_{-\infin}^{+\infin}e^{t(u^2+2\rho{uv}+v^2)}\mathrm{d}y \\\xlongequal{dv=\frac{1}{\sigma_2}dy} =\frac{1}{{2\pi}\sigma_1 \sqrt{1-\rho^2}} \int_{-\infin}^{+\infin}e^{t(u^2+2\rho{uv}+v^2)}\mathrm{d}v fX(x)=∫−∞+∞f(x,y)dy=2πσ1σ21−ρ21∫−∞+∞et(u2+2ρuv+v2)dydv=σ21dy=2πσ11−ρ21∫−∞+∞et(u2+2ρuv+v2)dv
-
t ( u 2 + 2 ρ u v + v 2 ) 中为了将 u 2 分离出去 , 同时使得剩余部分是一个平方形式 t ( ( u 2 ( 1 − ρ 2 ) + ρ 2 u 2 ) − 2 ρ u v + v 2 ) = − u 2 2 + t ( ρ 2 u 2 − 2 ρ u v + v 2 ) = − u 2 2 + t ( ( v − ρ u ) 2 ) = − u 2 2 − 1 2 ( 1 − ρ 2 ) ( ( v − ρ u ) 2 ) \\ t(u^2+2\rho{uv}+v^2)中为了将u^2分离出去, \\同时使得剩余部分是一个平方形式 \\ t((u^2(1-\rho^2)+\rho^2u^2)-2\rho{uv}+v^2) \\=-\frac{u^2}{2}+t(\rho^2u^2-2\rho{uv}+v^2) \\=-\frac{u^2}{2}+t((v-\rho{u})^2) \\=-\frac{u^2}{2}-\frac{1}{2(1-\rho^2)}((v-\rho{u})^2) t(u2+2ρuv+v2)中为了将u2分离出去,同时使得剩余部分是一个平方形式t((u2(1−ρ2)+ρ2u2)−2ρuv+v2)=−2u2+t(ρ2u2−2ρuv+v2)=−2u2+t((v−ρu)2)=−2u2−2(1−ρ2)1((v−ρu)2)
-
f X ( x ) = 1 2 π σ 1 e − u 2 2 ( 1 2 π 1 − ρ 2 ⋅ ∫ − ∞ + ∞ e − 1 2 ( 1 − ρ 2 ) ( ( v − ρ u ) 2 d v ) 记 Q = 1 2 π 1 − ρ 2 ⋅ ∫ − ∞ + ∞ e − 1 2 ( 1 − ρ 2 ) ( ( v − ρ u ) 2 这恰好符合一维随机变量正态分布的规范性表达式 , Q = 1 其中 : 随机变量取值 V ∼ ( μ , σ 2 ) ; σ = 1 − ρ 2 ; μ = ρ u ; f X ( x ) = 1 2 π σ 1 e − u 2 2 = 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 \\f_X(x)=\frac{1}{\sqrt{2\pi}\sigma_1} e^{-\frac{u^2}{2}} \left( \frac{1}{\sqrt{2\pi}\sqrt{1-\rho^2}} \cdot \int_{-\infin}^{+\infin} e^{-\frac{1}{2(1-\rho^2)}((v-\rho{u})^2}\mathrm{d}v \right) \\ 记Q=\frac{1}{\sqrt{2\pi}\sqrt{1-\rho^2}} \cdot\int_{-\infin}^{+\infin} e^{-\frac{1}{2(1-\rho^2)}((v-\rho{u})^2} \\这恰好符合一维随机变量正态分布的规范性表达式,Q=1 \\其中:随机变量取值V\sim(\mu,\sigma^2);\sigma=\sqrt{1-\rho^2};\mu=\rho{u}; \\f_X(x)=\frac{1}{\sqrt{2\pi}\sigma_1} e^{-\frac{u^2}{2}} =\frac{1}{\sqrt{2\pi}\sigma_1} e^{-\frac{({x-\mu_1})^2}{2\sigma_1^2}} fX(x)=2πσ11e−2u2(2π1−ρ21⋅∫−∞+∞e−2(1−ρ2)1((v−ρu)2dv)记Q=2π1−ρ21⋅∫−∞+∞e−2(1−ρ2)1((v−ρu)2这恰好符合一维随机变量正态分布的规范性表达式,Q=1其中:随机变量取值V∼(μ,σ2);σ=1−ρ2;μ=ρu;fX(x)=2πσ11e−2u2=2πσ11e−2σ12(x−μ1)2
-
类似的:
- f Y ( y ) = 1 2 π σ 2 e − v 2 2 = 1 2 π σ 2 e − ( y − μ 2 ) 2 2 σ 2 2 f_Y(y)=\frac{1}{\sqrt{2\pi}\sigma_2} e^{-\frac{v^2}{2}} =\frac{1}{\sqrt{2\pi}\sigma_2} e^{-\frac{({y-\mu_2})^2}{2\sigma_2^2}} fY(y)=2πσ21e−2v2=2πσ21e−2σ22(y−μ2)2
分布函数😊
- F X ( x ) = 1 2 π σ 1 2 ∫ − ∞ x e − 1 2 σ 1 2 ( x − μ 1 ) 2 F Y ( y ) = 1 2 π σ 2 2 ∫ − ∞ x e − 1 2 σ 2 2 ( y − μ 2 ) 2 F_X(x)=\frac{1}{\sqrt{2\pi}\sigma_1^2}\int_{-\infin}^{x}e^{-\frac{1}{2\sigma_1^2}{(x-\mu_1)^2}} \\ F_Y(y)=\frac{1}{\sqrt{2\pi}\sigma_2^2}\int_{-\infin}^{x}e^{-\frac{1}{2\sigma_2^2}{(y-\mu_2)^2}} FX(x)=2πσ121∫−∞xe−2σ121(x−μ1)2FY(y)=2πσ221∫−∞xe−2σ221(y−μ2)2
性质
-
对于: ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) (X,Y)\sim{N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)} (X,Y)∼N(μ1,μ2,σ12,σ22,ρ)
-
根据上面的推导,可以知道(X,Y)关于X,Y的密度函数是一维正态分布的密度函数
-
所有:
- X , Y 均服从一维正态分布 : X ∼ ( μ 1 , σ 1 2 ) Y ∼ ( μ 2 , σ 2 2 ) X,Y均服从一维正态分布: \\X\sim{(\mu_1,\sigma_1^2)} \\Y\sim{(\mu_2,\sigma_2^2)} X,Y均服从一维正态分布:X∼(μ1,σ12)Y∼(μ2,σ22)
-
独立性
- X 与 Y 相互独立的充要条件是 ρ = 0 X与Y相互独立的充要条件是\rho=0 X与Y相互独立的充要条件是ρ=0
二维随机变量函数的相关分布规律
-
∣ a b c d ∣ ≠ 0 则 ( a X + b Y , c X + d Y ) 也服从二维正态分布 a X + b Y 也服从一维正态分布 \\ \begin{vmatrix} a & b\\ c & d \end{vmatrix} \neq{0} \\则(aX+bY,cX+dY)也服从二维正态分布 \\aX+bY也服从一维正态分布 acbd =0则(aX+bY,cX+dY)也服从二维正态分布aX+bY也服从一维正态分布
-
X ∼ ( μ 1 , σ 1 2 ) Y ∼ ( μ 2 , σ 2 2 ) 且 X , Y 相互独立 , ( 否则没有后续结论 ) 那么 ρ = 0 , ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) \\X\sim{(\mu_1,\sigma_1^2)} \\Y\sim{(\mu_2,\sigma_2^2)} \\且X,Y相互独立,(否则没有后续结论) \\ 那么\rho=0, (X,Y)\sim{N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)} X∼(μ1,σ12)Y∼(μ2,σ22)且X,Y相互独立,(否则没有后续结论)那么ρ=0,(X,Y)∼N(μ1,μ2,σ12,σ22,ρ)
确定性和不确定性
-
边缘分布为正态分布的二维联合分布,未必是二维正态分布
- 例如 : f ( x , y ) = 1 2 π e − x 2 + y 2 2 ( 1 + sin x cos y ) = 1 2 π 1 2 π e − x 2 ⋅ e − y 2 ( 1 + sin x cos y ) = 1 2 π e − x 2 1 2 π e − y 2 ( 1 + sin x cos y ) F X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y = 1 2 π e − x 2 ∫ − ∞ + ∞ 1 2 π e − y 2 ( 1 + sin x cos y ) d y = 1 2 π e − x 2 ( ∫ − ∞ + ∞ 1 2 π e − y 2 d y + ∫ − ∞ + ∞ sin x cos y d y ) = 1 2 π e − x 2 ( ∫ − ∞ + ∞ 1 2 π e − y 2 d y + sin x ∫ − ∞ + ∞ cos y d y ) = 1 2 π e − x 2 ( 1 + 0 ) = 1 2 π e − x 2 这是个标准的正态分布 ( X ∼ N ( 0 , 1 ) ) 例如: \\f(x,y)=\frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}}(1+\sin{x}\cos{y}) \\={\frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt{2\pi}}}e^{-{x^2}}\cdot e^{-y^2}(1+\sin{x}\cos{y}) \\ =\frac{1}{\sqrt{2\pi}}e^{-{x^2}} \frac{1}{\sqrt{2\pi}}e^{-{y^2}} (1+\sin{x}\cos{y}) \\F_X(x)=\int_{-\infin}^{+\infin}f(x,y)dy \\ =\frac{1}{\sqrt{2\pi}}e^{-{x^2}} \int_{-\infin}^{+\infin}\frac{1}{\sqrt{2\pi}} e^{-{y^2}}(1+\sin{x}\cos{y})dy \\=\frac{1}{\sqrt{2\pi}}e^{-{x^2}} (\int_{-\infin}^{+\infin}\frac{1}{\sqrt{2\pi}} e^{-{y^2}}dy + \int_{-\infin}^{+\infin}\sin{x}\cos{y}\mathrm{d}y) \\ =\frac{1}{\sqrt{2\pi}}e^{-{x^2}} (\int_{-\infin}^{+\infin}\frac{1}{\sqrt{2\pi}} e^{-{y^2}}dy + \sin{x}\int_{-\infin}^{+\infin}\cos{y}\mathrm{d}y) \\=\frac{1}{\sqrt{2\pi}}e^{-{x^2}}(1+0) =\frac{1}{\sqrt{2\pi}}e^{-{x^2}} \\这是个标准的正态分布(X\sim{N(0,1)}) 例如:f(x,y)=2π1e−2x2+y2(1+sinxcosy)=2π12π1e−x2⋅e−y2(1+sinxcosy)=2π1e−x22π1e−y2(1+sinxcosy)FX(x)=∫−∞+∞f(x,y)dy=2π1e−x2∫−∞+∞2π1e−y2(1+sinxcosy)dy=2π1e−x2(∫−∞+∞2π1e−y2dy+∫−∞+∞sinxcosydy)=2π1e−x2(∫−∞+∞2π1e−y2dy+sinx∫−∞+∞cosydy)=2π1e−x2(1+0)=2π1e−x2这是个标准的正态分布(X∼N(0,1))
-
由于轮换对称 , 所以 f Y ( y ) 也还是标准正态分布 由于轮换对称,所以f_Y(y)也还是标准正态分布 由于轮换对称,所以fY(y)也还是标准正态分布
- 而 f ( x , y ) 显然不是二维正态分布 而f(x,y)显然不是二维正态分布 而f(x,y)显然不是二维正态分布
🎈正态分布的可加性
- PT_二维随机变量:正态分布的可加性_xuchaoxin1375的博客-CSDN博客