三. 微分方程

1. 概念理解

专业术语 ==> 大白话

微分方程 ==> 含导数 微分方程的阶 ==> 最高阶导数
微分方程的解 ==> x与y的关系式
微分方程通解 ==> 含任意常数
微分方程通解的阶 ==> 任意常数的个数
微分方程初始条件 ==> 通解确定了数字
微分方程特解 ==> 确定了初始条件的解

2. 求一阶微分方程的通解的方法

2.1 可分离变量法

对应方程：变量可分离的微分方程
适用题型：可整理成x和y两者 井水不犯河水 的式子
$$f(x)dx=g(y)dy$$
使用：左右两侧同时不定积分
$$\int f(x)dx=\int g(y)dy+C$$

2.2 换元法

对应方程：齐次微分方程
题型：若某一阶微分方程可以整理为：
$$\frac{dy}{dx}=f（\frac{y}{x}）$$

使用: 把y/x换成u,得到：
$$\frac{dy}{dx}=u+x\ast \frac{du}{dx}$$

2.3 公式法（线性）

对应方程：一阶线性微分方程
题型：可以整理为
$$y^{\prime }+p(x)y=0或者y^{\prime }+p(x)y=q(x)$$
使用：不定积分积出来的不需要再加常数C

2.4 变量替换（非线性）

• 对应方程：伯努利方程（别努力方程）

• 题型：
  $$y^{\prime }+p(x)y=q(x)y^n$$

• 使用：
  

3. 二阶微分方程的通解

Ay’’ + By’ + Cy = []

若系数中的ABC都是常数，则称二阶微分方程 为 二阶常系数微分方程。

齐次： Ay’’ + By’ + Cy = 0

非齐次： Ay’’ + By’ + Cy = f(x)

3.1 二阶常系数齐次微分方程的通解

1. 把系数A化成1,得到 y’’ + py’ + q = 0
2. 求解一元二次方程 r^2 + pr + q = 0，得到r1，r2 根据特征方程的解分三种情况
   • r1 != r2
     $$y=C_1{e}^{r_{1}x}+C_2{e}^{r_{2}x}$$
   • r1 = r2
     $$y=(C_1+C_{2}x)e^{r_{1}x}$$
   • 一对共轭 ： r1 = r2 = α ± β i
     $$y=(C_{1}cos\beta x+C_{2}sin\beta x)e^{\alpha x}$$

3.2 二阶常系数非齐次微分方程的通解

1. 先求出对应的齐次方程的解（假设右边是0）
2. 再求出非齐次的特解
3. 两者相加

• 技巧
  y1,y2,y3 是三个非齐特，那么 y1 - y2 以及 y2 - y3 是对应的齐次的解

3.3 二阶变系数微分方程的通解

Ay’’ + By’ + Cy = []

其中的A，B，C不全为数字，则称为二阶变系数微分方程

但从考研数学角度,仅有两种：

1. 不含y：把y’换成P，把y’‘换成P’
2. 不含x: 把y’换成P，把y’'换成P * dp/dy

求通解：可以含常数C
求表达式：不可以含常数C，得求出来。

• 经典问题：已知解，求对应的微分方程
  通过系数对应方程，直接得出结果。

4. 补充（知能行）

4.1 解题技巧：非齐次解的差为齐次解

4.2 建模与应用：未知函数的选择

4.3 解题技巧：非齐次方程解的叠加

4.4 解题技巧：f(x) = Asinβx的特解

4.5 基础知识：k重复根的设解

出现了三角函数、代表存在复数。
三角函数内的系数为复数的系数。
外圈出现了e的指数函数，则表示实数位置的系数。
k个重复的根、则x的指数为k-1。

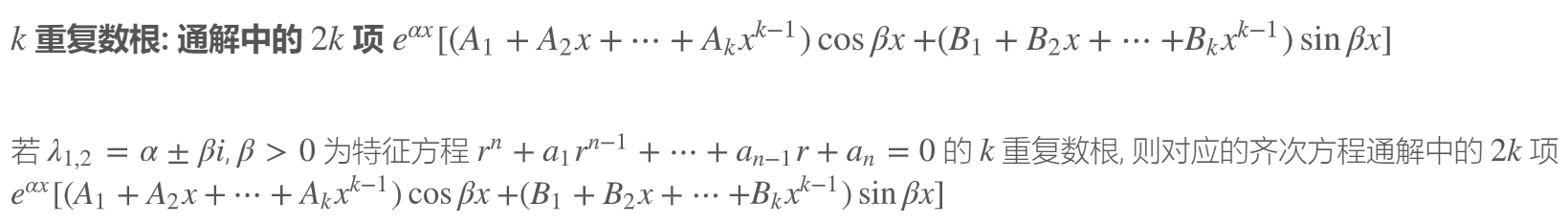
4.6 自由项对应的特征方程的根⭐

4.7 求解欧拉方程

核心：1）记住欧拉方程形式。2）理解怎么换元的。

4.8 解题技巧：三阶常系数微分方程

求解常系数齐次线性微分方程：先写出其特征方程, 求出特征根, 再根据特征根写出通解结构。

如果全是y及y的高阶导，不需要考虑换元，直接列特征方程！
例如：y″′-2y″+y′-2y=0
就不需要设置p = y′。
求得方程的特征根分别为：λ1=2，λ2=±i，
于是方程的基本解组为：e2x，cosx，sinx，
从而方程的通解为：
y(x)＝C1e2x+C2cosx+C3sinx，其中C1，C2，C3为任意常量。

5. 学习链接

1. 知乎：高阶常系数线性微分方程解法
2. CSDN博客：二阶常系数齐次线性微分方程的通解

6. 其他知识点的结合

6.1 抽象幂级数的和函数求解

与幂级数中和函数的结合，表面是求和函数，实际上需要构造和函数S(x)的微分方程，进而求解出S(x).

20年数一真题：

构造微分方程需要求导，所以写求S‘(x)，通过与S(x)的形式上的一致，构造等式。

至此解S’(x) = 1 + xS’(x) + 1/2 S(x) 的微分方程即可。