解方程AX=b与矩阵分解：奇异值分解（SVD分解） 特征值分解 QR分解 三角分解 LLT分解

article/2025/8/30 6:55:59

目录

1. 前言

1.1 为什么要进行矩阵分解？

1.2 矩阵与矩阵分解的几何意义？

2. LU三角分解

3. Cholesky分解 — LDLT分解

4. Cholesky分解 — LLT分解 

5. QR分解

6. 奇异值分解

7. 特征值分解

本文转自大佬博客：https://blog.csdn.net/Hansry/article/details/104174651

1. 前言

        本博客主要介绍在SLAM问题中常常出现的一些线性代数相关的知识，很早就想整理一下了，刚好看到Manii 的博客对矩阵分解的方法进行了总结，以方便求解线性方程组AX=B。在基于《计算机视觉—算法与应用》附录A 的内容 ，重点介绍了各种分解的适用情况、分解的特点。

1.1 为什么要进行矩阵分解？

        1、矩阵分解可以在一定程度上降低存储空间，可以大大减少问题处理的计算量（如对一个矩阵进行求逆、求解方程组等），从而高效地解决目标问题。
        2、矩阵分解可以提高算法的数值稳定性。

1.2 矩阵与矩阵分解的几何意义？

        在矩阵分解中，我们常常期望将矩阵分解成正交矩阵、对角矩阵以及上三角（下三角）矩阵的乘积。以三维矩阵为例，一个普通矩阵的几何意义是对坐标进行某种线性变换，而正交矩阵的几何意义是坐标的旋转，对角矩阵的几何意义是坐标的缩放，三角矩阵的几何意义是对坐标的切边。因此对矩阵分解的几何意义就是将这种变换分解成缩放、切边和旋转的过程。

2. LU三角分解

        三角分解又称为LU分解或LR分解，是将原正方（square）矩阵分解成一个上三角矩阵和一个下三角矩阵。

 其中L是单位下三角矩阵，D是对角矩阵，U是单位上三角矩阵。

3. Cholesky分解 — LDLT分解

        假设矩阵A为对称矩阵，且任意K阶主子式均不为0时(即正定)，A有如下唯一的分解形式：

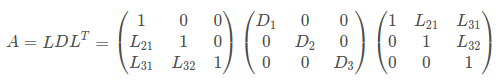
即L为下三角单位矩阵，D为对角矩阵。LDLT方法实际上是Cholesky分解法的改进（LLT分解需要开平方），具体代码可见Chelesky分解LDLT用于求解线性方程组。

注：一个对称矩阵A是正定的充要条件是对任何非零向量 x 有  ，即对称矩阵A正定，非奇异，也可以说任意K阶主子式均不为0。

 这里举个例子，比如VINS的初始化过程中，在做视觉sfm和IMU预积分的PVQ对齐的时候（即在initial_alignment.cpp文件中的LinearAlignment()函数中），会在对齐流程的第3步利用平移约束估计重力、速度和尺度初始值时用到ldlt来求解待优化的变量[v0, v1, ...vn, g, s]。构建H△x=b的形式进行优化参数求解，具体代码如下：

/*** @brief 求解各帧的速度，枢纽帧的重力方向，以及尺度* * @param[in] all_image_frame * @param[in] g * @param[in] x * @return true * @return false */
bool LinearAlignment(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)
{// 这一部分内容对照论文进行理解// 这里是《VIO 第7讲》 —— 视觉与IMU对齐估计流程第3步：利用平移约束估计重力、速度以及尺度初始值int all_frame_count = all_image_frame.size();int n_state = all_frame_count * 3 + 3 + 1;      // 速度 + 重力 + 尺度因子MatrixXd A{n_state, n_state};A.setZero();VectorXd b{n_state};b.setZero();map<double, ImageFrame>::iterator frame_i;map<double, ImageFrame>::iterator frame_j;int i = 0;for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i ++, i ++){frame_j = next(frame_i);MatrixXd tmp_A(6, 10);tmp_A.setZero();VectorXd tmp_b(6);tmp_b.setZero();double dt = frame_j->second.pre_integration->sum_dt;// 《VIO第7讲》，公式（17）tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();tmp_A.block<3, 3>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity();tmp_A.block<3, 1>(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;     tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0];// cout << "delta_p   " << frame_j->second.pre_integration->delta_p.transpose() << endl;tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;tmp_A.block<3, 3>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity();tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v;// cout << "delta_v   " << frame_j->second.pre_integration->delta_v.transpose() << endl;Matrix<double, 6, 6> cov_inv = Matrix<double, 6, 6>::Zero();// cov.block<6, 6>(0, 0) = IMU_cov[i + 1];// MatrixXd cov_inv = cov.inverse();cov_inv.setIdentity();MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();b.segment<6>(i * 3) += r_b.head<6>();A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();b.tail<4>() += r_b.tail<4>();A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();}// 增强数值稳定性A = A * 1000.0;b = b * 1000.0;x = A.ldlt().solve(b);      // 注意这里的求解方式是ldlt分解 △△△△△double s = x(n_state - 1) / 100.0;  // 取出尺度ROS_DEBUG("estimated scale: %f", s);g = x.segment<3>(n_state - 4);      // 取出重力ROS_DEBUG_STREAM(" result g     " << g.norm() << " " << g.transpose());// 做一些检查if(fabs(g.norm() - G.norm()) > 1.0 || s < 0){return false;}// 重力修复：《VIO第7讲》 —— 视觉与IMU对齐流程中第4步：对重力向量g_c0进行优化RefineGravity(all_image_frame, g, x);// 得到真实尺度s = (x.tail<1>())(0) / 100.0;(x.tail<1>())(0) = s;ROS_DEBUG_STREAM(" refine     " << g.norm() << " " << g.transpose());if(s < 0.0 )return false;   elsereturn true;
}

4. Cholesky分解 — LLT分解 

         LLT分解又被称为平方根分解，是LDLT分解的一种特殊形式，即其中的D为单位矩阵。

一个对称正定矩阵A可以唯一地被分解成一个下三角矩阵L和L的转置LT相乘的形式：

 其中的L是下三角矩阵，R是上三角矩阵。
(正定要求矩阵的所有特征值必须大于0，因此分解的下三角对角元也是大于0的）
LLT分解常用于求解最小二乘问题中的。

因子经过因子分解后，x 可以通过解下面的方程获得，即只需求解两个三角系统，通过一系列前向和后向迭代运算。 

LLT分解的总操作数为O (N2)，具体代码可见Chelesky分解LLT，对于系数矩阵来说操作数会大大降低。

5. QR分解

        如果A是mxn实（复）矩阵，且其n个列线性无关，则A有分解：

 

        QR分解有三种常用方法：Givens 变换、Householder 变换，以及 Gram-Schmidt正交化。
        QR分解是一项广泛用于稳定求解病态最小二乘问题的方法，也是一些更复杂算法的矩阵，如计算SVD及特征值分解。在计算机视觉中，QR分解可以用于将相机矩阵转换为一个旋转矩阵和一个上三角的标定矩阵。 

        这里比如ICP算法中求解R和t。

// 《SLAM14讲》SVD求解  P174
void pose_estimation_3d3d(const vector<Point3f>& pts1,const vector<Point3f>& pts2,Mat& R, Mat& t)
{Point3f p1, p2;                     // center of mass  质心int N = pts1.size();for(int i=0; i<N; i ++){p1 += pts1[i];p2 += pts2[i];}p1 = Point3f ( Vec3f(p1) / N );p2 = Point3f ( Vec3f(p2) / N );vector<Point3f> q1(N), q2(N);       // remove the center，去中心化之后的点for(int i=0; i<N; i ++){q1[i] = pts1[i] - p1;q2[i] = pts2[i] - p2;}// compute q1*q2^T 求出《SLAM14讲》P174页的 WEigen::Matrix3d W = Eigen::Matrix3d::Zero();for(int i=0; i<N; i ++){W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();}cout << "W = " << W << endl;// SVD on WEigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeThinV);Eigen::Matrix3d U = svd.matrixU();      // 得到U矩阵Eigen::Matrix3d V = svd.matrixV();      // 得到V矩阵// 第2帧到第1帧的变换，与PnP中第1    determinant行列式if( U.determinant() * V.determinant() < 0 ){for(int x=0; x < 3; x ++){U(x, 2) *= -1;}}cout << "U = " << U << endl;cout << "V = " << V << endl;Eigen::Matrix3d R_ = U * (V.transpose());Eigen::Vector3d t_ = Eigen::Vector3d( p1.x, p1.y, p1.z ) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);      // P174页 式7.53 t* = p - R p'// convert to cv::Mat 将矩阵和向量统一转换为转换为Mat矩阵形式R = (Mat_<double> (3,3) <<R_(0,0), R_(0,1), R_(0,2),R_(1,0), R_(1,1), R_(1,2),R_(2,0), R_(2,1), R_(2,2));t = (Mat_<double>(3,1) <<t_(0,0), t_(1,0), t_(2,0));
}

6. 奇异值分解

        设A是一个mxn的矩阵，则存在一个分解的m阶正交矩阵U、非负对角阵Σ和n阶正交矩阵V：

在这里插入图片描述

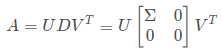
        其中Σ = d i a g ( σ 1 , σ 2 , . . . , σ r ) ，σ 为矩阵A的全部非零奇异值，且一般我们会将Σ 的值从大到小排序。奇异值分解的一个重要性质是：在实际大多数情况中，奇异值σ 减小的速度特别快，因此可以使用前r  个奇异值来对矩阵做近似（即丢弃U和V的后几列），将获得原始矩阵A在最小二乘意义下的最佳逼近。

        矩阵的奇异值分解通常是不唯一的。
        SVD分解在最优化问题、特征值问题、最小二乘问题（尤其是亏秩最小二乘问题）等具有巨大的作用。
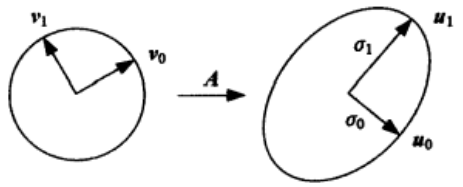
        SVD分解的几何意义可以通过公式的重写获得：

另一种解释为：当一个矩阵A作用于一个向量时，由于矩阵A可以被分解为正交矩阵、对角矩阵、正交矩阵，因此可以理解为对该向量先旋转、再缩放，然后再旋转。 

7. 特征值分解

        如果A是一个NxN的方阵，且有N个线性无关的特征向量，则可以被写成特征值分解的形式：

        其中U为NxN方阵，且第i 列为 A 的特征向量，Λ 为对角矩阵，其对角线上的元素为对应的特征值。注意只有可对角化矩阵才能作特征值分解。

        特征值分解可用于求解矩阵的逆：

        在数据统计分析中常常出现A为半正定矩阵，其表示数据点的协方差，此时特征值分解就是通常所说的主分量分析（PCA），因为它完成了对数据点分布在其中心周围变化的主方向和幅度的建模。 

        在求解最小二乘问题时，常常通过一系列外积之和构造对称矩阵C，此时C也是半正定的：

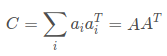
此时C的特征值和特征向量与A的奇异值和奇异向量：

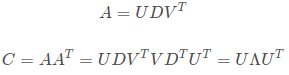
由此我们可以得到特征值。

        对称矩阵：任意的 N×N 实对称矩阵都有 N 个线性无关的特征向量。并且这些特征向量都可以正交单位化而得到一组正交且模为 1 的向量。故实对称矩阵 A 可被分解成 A=UΛU，其中 U 为 正交矩阵， Λ 为实对角矩阵，因此一个实对称矩阵有实特征值，其特征向量两两正交。—《多视图几何》附录A4.2


http://chatgpt.dhexx.cn/article/uOsGvbGH.shtml

相关文章

基于gtest、mockcpp写C++LLT测试入门级教程

基于gtest、mockcpp写C++LLT测试入门级教程

一、googletest 下载地址&#xff1a;https://github.com/google/googletest 编译googletest: 在根目录下执行 cmake . make 编译出的libgtest.a后面用 注意&#xff1a;有可能编译会失败&#xff0c;是gtest需要C11以上 可以在顶级的CMakeList.txt里加入 set(CMAKE_CXX_STA…
阅读更多...
量化策略分享 | MA超进化：LLT低延迟趋势线

量化策略分享 | MA超进化：LLT低延迟趋势线

移动平均线&#xff08;MA&#xff09;是我们技术分析中常用的一种趋势跟踪指标&#xff0c;但在使用的时候你是否也会有这样的烦恼&#xff1a;交易信号延迟太久&#xff0c;或者交易信号太频繁了&#xff01;延迟性和平滑性问题似乎是不可兼得的“鱼和熊掌”。 针对这个问题&…
阅读更多...
LLT-发现股市中的“大浪”

LLT-发现股市中的“大浪”

引言&#xff1a; 股市中小的波动经常干扰股票投资人对大趋势的判断&#xff0c;倘若股市的波动同信号波动类似&#xff0c;那是不是可以用处理信号的方式处理股票波动发现大的波动呢&#xff1f;我们知道通信领域在处理信号波动时也常会遇到被噪音干扰的问题&#xff0c;这些噪…
阅读更多...
HDU2544 最短路dij

HDU2544 最短路dij

纯最短路。 1 ///HDU 2544堆优化的最短路2 #include <cstdio>3 #include <iostream>4 #include <sstream>5 #include <cmath>6 #include <cstring>7 #include <cstdlib>8 #include <string>9 #include <vector>10 #include &l…
阅读更多...
dij算法堆优化_迪杰斯特拉算法(Dijkstra) （基础dij+堆优化） BY：优少(示例代码)...

dij算法堆优化_迪杰斯特拉算法(Dijkstra) （基础dij+堆优化） BY：优少(示例代码)...

算法实现步骤&#xff1a; a.初始时&#xff0c;只包括源点&#xff0c;即S {v}&#xff0c;v的距离为0。U包含除v以外的其他顶点&#xff0c;即&#xff1a;U {其余顶点}&#xff0c;若v与U中顶点u有边&#xff0c;则(u,v)为正常权值&#xff0c;若u不是v的出边邻接点,则(u,v…
阅读更多...
dij算法堆优化_迪杰斯特拉算法(Dijkstra) （基础dij+堆优化） BY：优少

dij算法堆优化_迪杰斯特拉算法(Dijkstra) （基础dij+堆优化） BY：优少

算法实现步骤&#xff1a; a.初始时&#xff0c;只包括源点&#xff0c;即S {v}&#xff0c;v的距离为0。U包含除v以外的其他顶点&#xff0c;即&#xff1a;U {其余顶点}&#xff0c;若v与U中顶点u有边&#xff0c;则(u,v)为正常权值&#xff0c;若u不是v的出边邻接点,则(u,v…
阅读更多...
图的最短路径——DIJ算法，有向图的矩阵实现，图的基本操作

图的最短路径——DIJ算法，有向图的矩阵实现，图的基本操作

图是一种非常重要的数据结构&#xff0c;在研究从一点出发到各个顶点的最短距离。 实验目的 1. 掌握图的基本概念、表示方法、遍历方法。 2. 掌握图的最短路径算法。 实验要求 1&#xff0e; 输入图的顶点数n&#xff08;不超过10个&#xff09;、边数m&#xff0c;顶点分…
阅读更多...
堆优化dij

堆优化dij

模板 【算法介绍】 用一个优先级队列来记录点和dis值&#xff0c;按照顺序进行边的松弛即可 1.农场派对 【题意】 有向图&#xff0c;求1-n所有点中到x点一去一回的最短路的最大值 【分析】 建立原图和反图&#xff0c;以x为源点跑两次dijkstra&#xff0c;对于1-n每个点…
阅读更多...
图中的搜索——dij

图中的搜索——dij

Dijkstra(迪杰斯特拉算法)常常用于求解图中的单点最短路径问题。其主要实现方法可拆分为两个步骤&#xff1a;①更新距离信息②找出当前最小路径 如下图所示&#xff0c;要求求出1结点到6结点的最短路径。 我们可以先定义一下重点内容&#xff1a; 邻接矩阵map[i][j]&#xf…
阅读更多...
关于普通dij算法为什么不能解决负权边的分析

关于普通dij算法为什么不能解决负权边的分析

我们首先来分析下含负权边的无向图&#xff1a; 1.先看图 我们求A点到C点的最短距离&#xff0c;很明显答案为1. 2.我们用dij来跑下&#xff0c;看过程&#xff1a; 先把A点标记哈&#xff0c;不需要访问本身首先找到距A最近的且直接相连的点&#xff08;也就是两点间没有…
阅读更多...
dij最短路+堆优化

dij最短路+堆优化

dij一个主要思路&#xff0c;将所有点分为两个集合S&#xff0c;T&#xff0c;初始集合S中只包含了起点&#xff0c;T集合包含所有点&#xff0c;要做的就是从T集合中不断选取与S集合中的点距离最短的并且未被加入S集合中的点&#xff0c;将这个点加入S集合&#xff0c;并用这个…
阅读更多...
FreeType移植到 STM32 单片机以支持矢量字体

FreeType移植到 STM32 单片机以支持矢量字体

目录 一、准备工作 二、复制文件 三、添加C文件到Keil中 四、修改接口 五、调用 六、优化 七、效果 一、准备工作 下载Freetype源码 ----- 下载FreeType 以移植到Keil 的STM32工程为例 移植前的软件环境&#xff1a; 1&#xff0c;实现了内存分配函数 2&#xff0c;实现了文件…
阅读更多...
freetype库实现文字显示

freetype库实现文字显示

原文&#xff1a;http://www.cnblogs.com/lifexy/p/8503070.html 1 .数码相框-通过freetype库实现矢量显示 本章主要内容如下: 1)矢量字体原理2)使用freetype库实现矢量字体显示 1. 矢量字体原理 将汉字的笔划边缘用直线段描述成封闭的曲线&#xff0c;并将线段各端点的坐标经压…
阅读更多...
常用字体介绍（freetype）

常用字体介绍（freetype）

字体显示原理 字体和图片一样&#xff0c;存储为像素&#xff0c;绘制的时候需要找到字体对应的像素显示 字体文件格式 ttf&#xff0c;只包含一种字体格式&#xff0c;矢量字体ttc&#xff0c;ttc包含多个ttf文件&#xff0c;包含多种字体格式otf&#xff0c;ttf的扩展&…
阅读更多...
FreeType 简单使用

FreeType 简单使用

FreeType 2 第一步 &#xff0d;&#xff0d; 简易的字形装载 介绍 这是“FreeType2 教程”的第一部分。它将教会你如何&#xff1a; * 初始化库 * 通过创建一个新的 face 对象来打开一个字体文件 * 以点或者象素的形式选择一个字符大小 * 装载一个字形(glyph)图像&…
阅读更多...
freetype的安装与使用

freetype的安装与使用

一、在PC上的安装与使用 1) 开发环境 系统版本&#xff1a; ubuntu14.04 freetype版本&#xff1a; freetype-2.4.10 gcc版本&#xff1a; gcc version 4.8.4 (Ubuntu 4.8.4-2ubuntu1~14.04.3) 2) 步骤 1. 解压缩 tar xjf freetype-2.4.10.tar.bz2 2. 配置 …
阅读更多...
freetype环境安装记录

freetype环境安装记录

&#xff08;一&#xff09;摘要 最近在学习韦东山老师的驱动入门课程&#xff0c;在freetype环境安装时碰到到了一下这个报错&#xff0c;于是想记录下自己的安装过程方便其他碰到问题的同学解决&#xff01; &#xff08;二&#xff09;碰到的报错 我是用的是IMX6ULL PRO开…
阅读更多...
freetype的简单使用

freetype的简单使用

安装完毕以后我们先做个简单的实例程序看看效果 1.首先先下载字体 链接&#xff1a;https://pan.baidu.com/s/1FCOh9SYcVkYCkaT6wtXWtA 提取码&#xff1a;rohm 2.编写程序 编译测试文件example.c /*编译命令*/ -I指定库文件所在位置-L指定动态库位置gcc example.c…
阅读更多...
（转）FreeType字体位图属性

（转）FreeType字体位图属性

原文链接&#xff1a;https://blog.csdn.net/wlk1229/article/details/92424456 从原文中摘取一部分记录如下&#xff1a; FreeType获取的位图是一张刚好包含文字的位图&#xff0c;不包含左右上下的空白信息。如果绘制文字时直接把每一张位图连接在一起&#xff0c;文字则会一…
阅读更多...
freetype编译

freetype编译

freetype简介 FreeType库是一个完全免费(开源)的、高质量的且可移植的字体引擎&#xff0c;它提供统一的接口来访问多种字体格式文件&#xff0c;包括TrueType, OpenType, Type1, CID, CFF, Windows FON/FNT, X11 PCF等。支持单色位图、反走样位图的渲染。FreeType库是高度模块…
阅读更多...
推荐文章

Copyright @ 2022~2023