引言:
股市中小的波动经常干扰股票投资人对大趋势的判断,倘若股市的波动同信号波动类似,那是不是可以用处理信号的方式处理股票波动发现大的波动呢?我们知道通信领域在处理信号波动时也常会遇到被噪音干扰的问题,这些噪音通常需要用对应的滤波器过滤,那么在股市中我们是不是也可以设计合适的滤波器来过滤小的波动留下股市“大浪”呢?本文介绍的LLT模型就是基于此思想产生的。本文参考对象是广发证券的《低延迟趋势线与交易性择时——短线择时策略研究之三》,有兴趣更深入理解LLT原理的读者可以阅读原研报。
前言:
股票应该怎么交易?不就是低点买入高点卖出吗。
理想中的股票波动大致是这样的: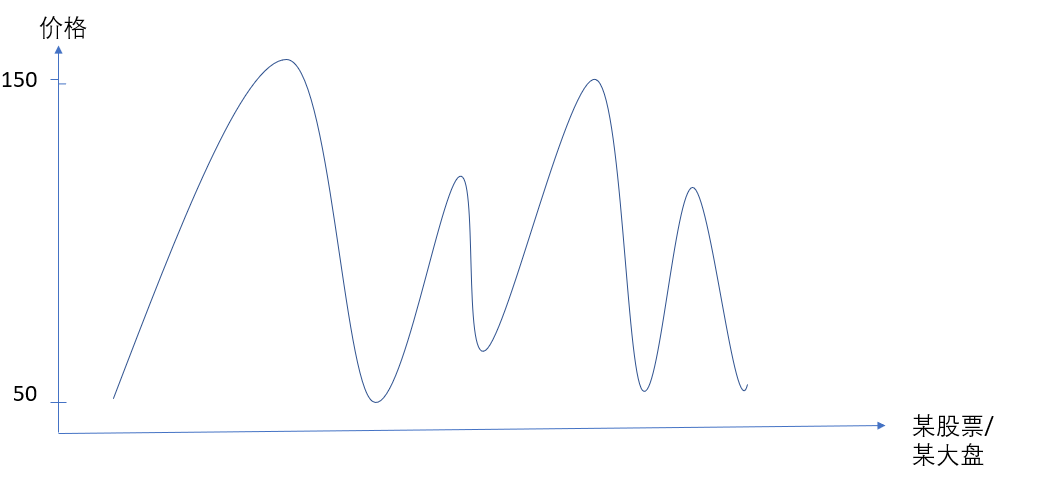
然后,理想的交易状态状态是这样的: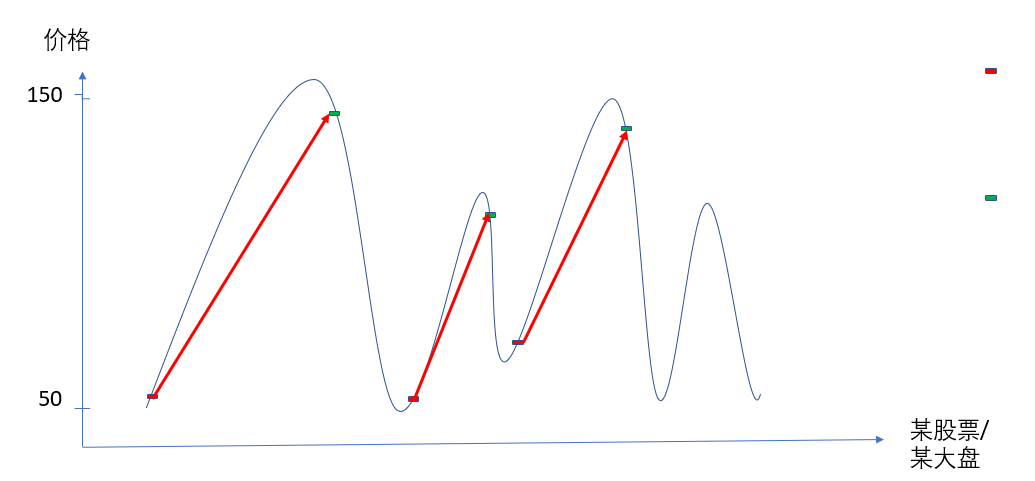
图一
图一图一
在有上涨趋势出现的时候买入,下跌趋势出现的时候卖出,稍微滞后一点没关系,总体肯定会赚的。
那么是不是从此资产飙升,过上睡觉睡到自然醒,数钱数到手抽筋的生活。然而,事实总是这样的:
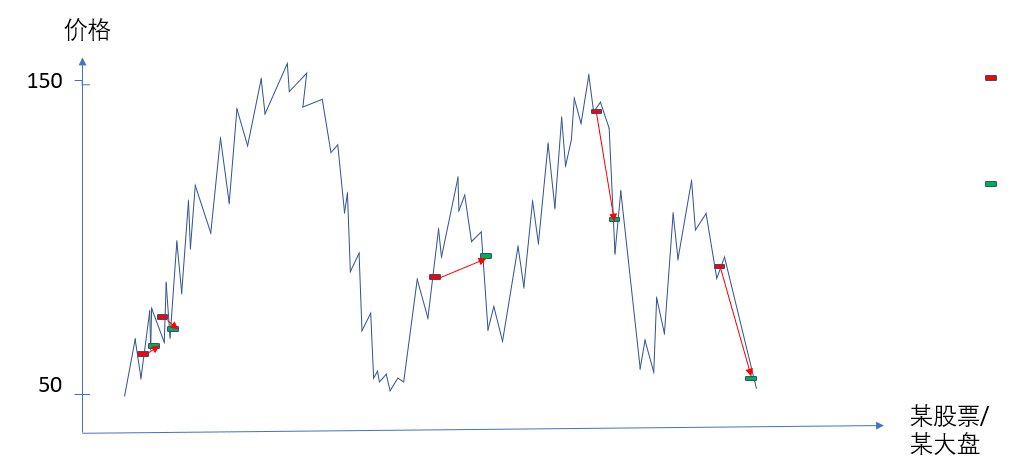
图二
图二图二
说好的一起做手拉手做一辈子的朋友呢?友谊的小船怎么说翻就翻?这些小波浪该怎么整!!!!
只有对大的趋势判断准确,才能规避掉股市中的小的波动,那么怎样作出正确的大趋势判断,来更好的的择时呢?这就是本文策略要解决的目标。本文的主角LLT趋势线(滤波器)为此而生。
正文:
1, MA,EMA指标
先从现有的择时策略引入,MA是一种常用的趋势跟踪指标,可以在一定程度上把图二转化为图一,MA的计算天数越长,曲线越平滑,过滤小“波浪”能力越强。但同时滞后性也越高,往往在股市最高最低点出现若干天后,MA才真正反应,这在震荡横盘的市场中劣势及其明显。
与MA类似的指标还有EMA,EMA计算的是过去数据的加权均值,并通过赋予邻近点更大的权重来提高指标的灵敏度。把 EMA的公式用通信的角度解释,EMA就是一个一阶低通滤波器,用以过滤高频率的波动留下低频率的波动。那么假设股价波动同样也是波动的这一假设成立,那么我们是不是可以利用通信领域常年积累的滤波器原理设计一个比EMA更加平滑灵敏的滤波器来实现引言中图一到图二的转化呢?本文讲述的LLT就是这样一个2阶滤波器。
2,LLT思路简介
LLT滤波器是广发证券短线择时研报提出的一种滤波器,旨在过滤股市中的低频波动留下高频波动,以便择时,是一种2阶的滤波器。
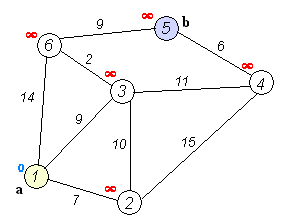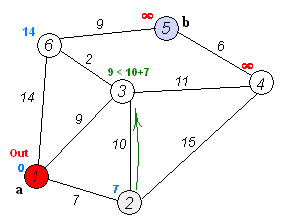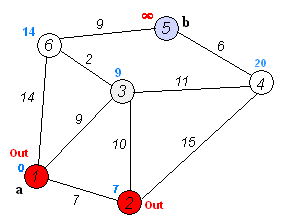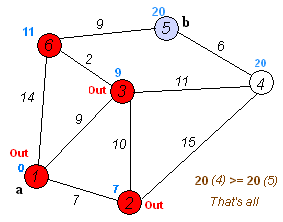
这一趋势跟踪策略的核心思路是把股市波动当做我们平时所见的信号波处理。信号传输过程中经常被噪音所干扰,所以通信领域大量使用滤波器函数来过滤不需要的频率的波动。若要发现股市中的“大浪”,我们需要把高频率的“小浪”过滤掉,于是股市趋势跟踪策略在通信领域就被转化成寻找股市波动中表现优良的滤波器的任务。(过高频波动留下低频波动的滤波器)
3,LLT模型的理解
通信领域习惯于过滤高频或低频的信号波,用以过滤噪音。首先我们用很多人熟悉的EMA公式来引入LLT模型。
1,EMA(1阶滤波器)引入:
指数平均线EMA:
textEMA(t)=α∗textprice(T)+(1−α)∗textEMA(t−1)
textEMA(t)=α∗textprice(T)+(1−α)∗textEMA(t−1)textEMA(t)=α∗textprice(T)+(1−α)∗textEMA(t−1)
(1)
其中EMA(1)=Price(1)EMA(1)=Price(1)EMA(1)=Price(1),ααα是一个取值在 0 到 1 之间的比例,EMA本质上是赋予邻近点更大权重比例的移动平均值数据
由于我们认为一个特定的波是由不同频率的波组合而成,所以一个随时间波动的波也可以表述成多个频率波动的组合,及自变量由时间(时域)变成了不同波的频率(频域)。我们可以用一个Z变换来将这一时域公式转化为频域公式
Z变换的公式是:
F(z)=∑k=−∞∞f(k)∗z−k
F(z)=∑k=−∞∞f(k)∗z−kF(z)=∑k=−∞∞f(k)∗z−k
其中 z 定义复频域,f(k)是时域离散信号,
接着定义传输函数:
H(z)=textEMA(z)textprice(z)
H(z)=textEMA(z)textprice(z)H(z)=textEMA(z)textprice(z)
(2)
在这顺便一提传输函数,传输函数是是指零初始条件下线性系统响应(即输出)量的拉普拉斯变换(或z变换)与激励(即输入)量的拉普拉斯变换之比。传输函数代表了输入和输出之间的联系,不受输入输出值的影响,可以用它来分析系统的动态特性,稳定性,或根据给定要求设计满意的控制器。
将(2)带入(1)式,并借助Z变换的线性性质:
a1f1(k)+a2f2(k)↔a1F1(k)+a2F2(k)
a1f1(k)+a2f2(k)↔a1F1(k)+a2F2(k)a1f1(k)+a2f2(k)↔a1F1(k)+a2F2(k)
和时位移性质:
f(k−m)↔z−mF(z)
f(k−m)↔z−mF(z)f(k−m)↔z−mF(z)
可以推导出EMA均线的传输函数为:
H1(z)=α1−(1−α)∗z−1
H1(z)=α1−(1−α)∗z−1H1(z)=α1−(1−α)∗z−1
这样就实现了EMA的时域频域转化。
2,LLT的设计
LLT是一个二阶的滤波器,广发证券此研报作者做了三部转化将EMA一阶滤波器转化为LLT二阶滤波器:
1, 为了使构造的高通滤波器,即不存在高频分量输出的1−H(z)1−H(z)1−H(z),首先修改EMA公式为:
textEMA′(T)=α∗textprice(T)+textprice(T−1)2+(1−α)∗textEMA′(T−1)
textEMA′(T)=α∗textprice(T)+textprice(T−1)2+(1−α)∗textEMA′(T−1)textEMA′(T)=α∗textprice(T)+textprice(T−1)2+(1−α)∗textEMA′(T−1)
接着我们将公式转换至频域以便于进行滤波,那么修改后的EMA滤波器变为
H2(z)=α∗(1+z−1)/21−(1−α)∗z−1
H2(z)=α∗(1+z−1)/21−(1−α)∗z−1H2(z)=α∗(1+z−1)/21−(1−α)∗z−1
2, 构建一阶高通滤波器,其结构为
H3(z)=1−H2(z)=(1−α/2)∗(1−z−1)1−(1−α)∗z−1
H3(z)=1−H2(z)=(1−α/2)∗(1−z−1)1−(1−α)∗z−1H3(z)=1−H2(z)=(1−α/2)∗(1−z−1)1−(1−α)∗z−1
3, 完成二阶滤波函数的构建
H4(z)=H3(z)∗H3(z)=(1−α/2)∗(1−2z−1+z−2)1−2(1−α)∗z−1+(1−α)2z−2
H4(z)=H3(z)∗H3(z)=(1−α/2)∗(1−2z−1+z−2)1−2(1−α)∗z−1+(1−α)2z−2H4(z)=H3(z)∗H3(z)=(1−α/2)∗(1−2z−1+z−2)1−2(1−α)∗z−1+(1−α)2z−2
相应的,对应的2阶高通滤波器为:
H5(z)=1−H4(z)=(α−α2/4)+(α2/2)z−1−(α−3α2/4)z−21−2(1−α)∗z−1+(1−α)2z−2
H5(z)=1−H4(z)=(α−α2/4)+(α2/2)z−1−(α−3α2/4)z−21−2(1−α)∗z−1+(1−α)2z−2H5(z)=1−H4(z)=(α−α2/4)+(α2/2)z−1−(α−3α2/4)z−21−2(1−α)∗z−1+(1−α)2z−2
最终得到了二阶高通滤波函数:
LLT(t)textprice(z)=1−H4(z)=(α−α2/4)+(α2/2)z−1−(α−3α2/4)z−21−2(1−α)∗z−1+(1−α)2z−2
LLT(t)textprice(z)=1−H4(z)=(α−α2/4)+(α2/2)z−1−(α−3α2/4)z−21−2(1−α)∗z−1+(1−α)2z−2LLT(t)textprice(z)=1−H4(z)=(α−α2/4)+(α2/2)z−1−(α−3α2/4)z−21−2(1−α)∗z−1+(1−α)2z−2
最后由拉普拉斯逆转换得到的 LLT(t)的公式为
LLT(t)=1−H4(z)=(α−α2/4)textprice(t)+(α2/2)textprice(t−1)−(α−3α2/4)textprice(t−2)+2(1−α)LLT(t-1)−(1−α)2LLT(t-2)
LLT(t)=1−H4(z)=(α−α2/4)textprice(t)+(α2/2)textprice(t−1)−(α−3α2/4)textprice(t−2)+2(1−α)LLT(t-1)−(1−α)2LLT(t-2)LLT(t)=1−H4(z)=(α−α2/4)textprice(t)+(α2/2)textprice(t−1)−(α−3α2/4)textprice(t−2)+2(1−α)LLT(t-1)−(1−α)2LLT(t-2)
理论上讲LLT就是原波动从前言中图二到图一的转化,及我们应该在LLT值大于LLT的上一值时大趋势来临,买入股票:当LLT值小于LLT前值时大趋势变为下降,卖出股票。
4,HS300应用
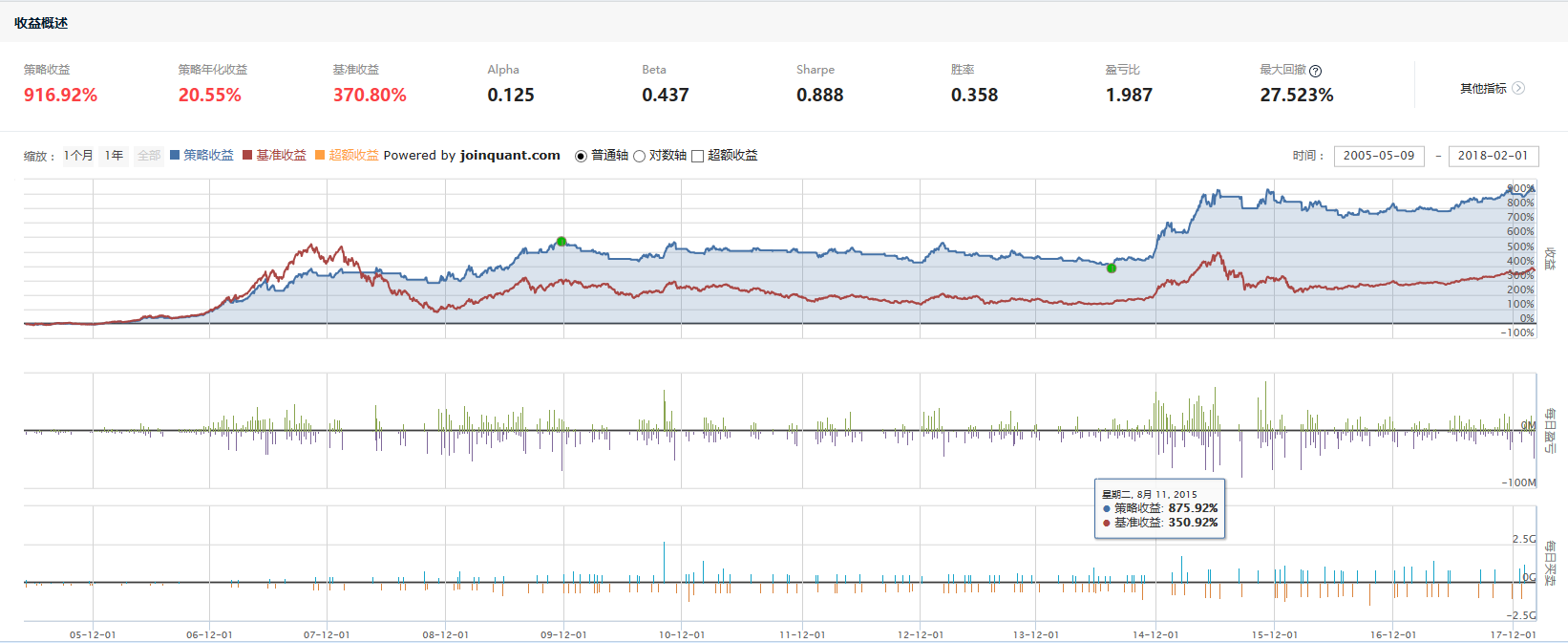
LLT策略的参数只有alpha一个。在HS300中本文用梯度下降的方法将alpha调整为2/35.
此图是无交易费用的策略表现,从2005年至今,年化收益20%,回撤27.5%,表现尚可吧。后面附代码是加入了交易费用后的表现,年化收益将至17%。总的来说这一策略预防股灾的效果尚可。
5,补充和扩展
LLT本质上只是一种滤波器罢了,某些邮电学校通信工程专业仓库里不要的滤波器函数一抓一大把,是不是可以废物利用一下试试股市上好不好用呢?只恨当年没学好通信原理啊!(哭晕在厕所)
小编个人感觉择时策略有较好的预测股灾能力,虽然大部分收益一般,但可以作为其他选股策略的止损函数,从而获得其他策略高收益的同时降低风险。另一个大盘择时策略RSRS效果也不错,推荐大家阅读。此外,聚宽论坛上也有很多择时模型,有兴趣的读者可以继续研究。
本文由JoinQuant量化课堂推出,版权归JoinQuant所有,商业转载请联系我们获得授权,非商业转载请注明出处。文章更迭记录:
v1.0,2018-02-16,文章上线
v1.1,2018-03-16,增加代码中LLT1,LLT2的注释