模板
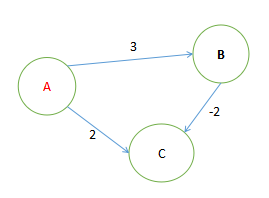
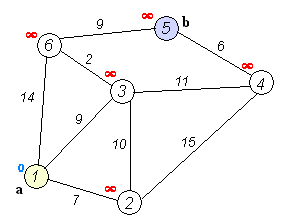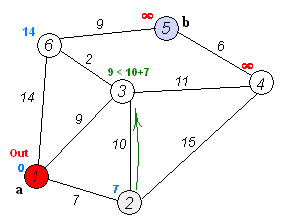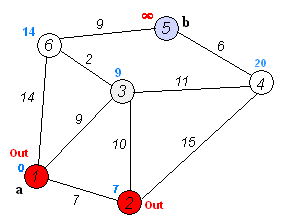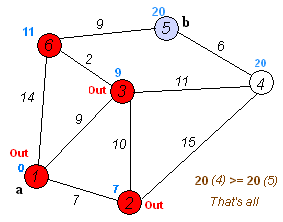
【算法介绍】
用一个优先级队列来记录点和dis值,按照顺序进行边的松弛即可
1.农场派对
【题意】
有向图,求1-n所有点中到x点一去一回的最短路的最大值
【分析】
建立原图和反图,以x为源点跑两次dijkstra,对于1-n每个点的两个dis之和取最大即可
【代码】
#include<bits/stdc++.h>
using namespace std;
int n,m,xx;
const int maxn=1e3+5;
const int maxm=1e5+5;
int head[maxn],tot;
struct edge
{int to,nxt,v;
}e[maxm],g[maxm];
void add(int x,int y,int z)
{e[++tot].to=y; e[tot].nxt=head[x]; e[tot].v=z; head[x]=tot;
}
int h[maxn],cnt;
void addedge(int x,int y,int z)
{g[++cnt].to=y; g[cnt].nxt=h[x]; g[cnt].v=z; h[x]=cnt;
}
int dis[maxn],vis[maxn],diss[maxn],viss[maxn];
const int inf=0x3f3f3f3f;
void dij()
{priority_queue <pair<int,int> > q;for(int i=0;i<=n;i++) dis[i]=inf;q.push(make_pair(0,xx)); dis[xx]=0;vis[xx]=1;while(!q.empty()){int u=q.top().second;q.pop();for(int i=head[u];i;i=e[i].nxt){int to=e[i].to;if(dis[to]>dis[u]+e[i].v){dis[to]=dis[u]+e[i].v;if(!vis[to]){q.push(make_pair(-dis[to],to));vis[to]=1;}}}vis[u]=0;}
}
void dijj()
{priority_queue <pair<int,int> > q;for(int i=0;i<=n;i++) diss[i]=inf;q.push(make_pair(0,xx)); diss[xx]=0;viss[xx]=1;while(!q.empty()){int u=q.top().second;q.pop();for(int i=h[u];i;i=g[i].nxt){int to=g[i].to;if(diss[to]>diss[u]+g[i].v){diss[to]=diss[u]+g[i].v;if(!viss[to]){q.push(make_pair(-diss[to],to));viss[to]=1;}}}viss[u]=0;}
}
int main()
{freopen("a.in","r",stdin);freopen("a.out","w",stdout);scanf("%d%d%d",&n,&m,&xx);for(int i=1;i<=m;i++){int x,y,z;scanf("%d%d%d",&x,&y,&z);add(x,y,z); addedge(y,x,z);}dij();dijj();int ans=-inf;for(int i=1;i<=n;i++)ans=max(ans,dis[i]+diss[i]);printf("%d",ans);return 0;
}
2.Roadblocks (次短路问题)
【题意】
无向图,求次短路
【分析】
这个也是十分经典的一个题了
我们需要记录一个dis[]表示1-i的最短路,还要记录一个1-i的第二短的路径长度
更新方式和正常的dijkstra很相似,注意更新时dis2=u.first+e[i].v 调了好久........
这里之所以必须用u.first的原因是:
1-i的次短路可能由两种情况转移来,一种是1-j的最短路+e[j][i],另一种是i-j的次短路+e[j][i],这两种情况都要兼顾,所以用u.first区分他是从那种转移来的
【代码】
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int maxn=5e3+5;
const int maxm=1e5+5;
int head[maxn],tot;
struct edge
{int to,nxt,v;
}e[maxm<<1];
void add(int x,int y,int z)
{e[++tot].to=y; e[tot].nxt=head[x]; e[tot].v=z; head[x]=tot;
}
int dis[maxn],vis[maxn],diss[maxn];
const int inf=0x3f3f3f3f;
void dij()
{priority_queue <pair<int,int> > q;for(int i=1;i<=n;i++) dis[i]=inf,diss[i]=inf;q.push(make_pair(0,1)); dis[1]=0;while(!q.empty()){int u=q.top().second,v=-q.top().first;q.pop();if(diss[u]<v) continue;for(int i=head[u];i;i=e[i].nxt){int to=e[i].to;int dis2=v+e[i].v;if(dis[to]>dis2){swap(dis[to],dis2);q.push(make_pair(-dis[to],to));}if(diss[to]>dis2 && dis[to]<dis2){diss[to]=dis2;q.push(make_pair(-diss[to],to));}}}
}
int main()
{freopen("a.in","r",stdin);freopen("a.out","w",stdout);scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int x,y,z;scanf("%d%d%d",&x,&y,&z);add(x,y,z); add(y,x,z);}dij();printf("%d",diss[n]);return 0;
}3.最短路计数
【题意】
给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1∼N。问从顶点 1 开始,到其他每个点的最短路有几条。
【分析】
dijkstra当dis相等时更新一下cnt即可
【代码】
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int maxn=1e5+5;
const int maxm=2e5+5;
int head[maxn],tot;
struct edge
{int to,nxt,v;
}e[maxm<<1];
void add(int x,int y,int z)
{e[++tot].to=y; e[tot].nxt=head[x]; e[tot].v=z; head[x]=tot;
}
int dis[maxn],cnt[maxn];
const int inf=0x3f3f3f3f;
const int mod=100003;
void dij()
{priority_queue <pair<int,int> > q;for(int i=1;i<=n;i++) dis[i]=inf;q.push(make_pair(0,1)); dis[1]=0; cnt[1]=1;while(!q.empty()){int u=q.top().second;q.pop();for(int i=head[u];i;i=e[i].nxt){int to=e[i].to;if(dis[to]>dis[u]+e[i].v){dis[to]=dis[u]+e[i].v;cnt[to]=cnt[u];q.push(make_pair(-dis[to],to));}else if(dis[to]==dis[u]+e[i].v)cnt[to]=(cnt[to]+cnt[u])%mod;}}
}
int main()
{freopen("a.in","r",stdin);freopen("a.out","w",stdout);scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);add(x,y,1); add(y,x,1);}dij();for(int i=1;i<=n;i++)printf("%d\n",cnt[i]);return 0;
}