dij最短路+堆优化

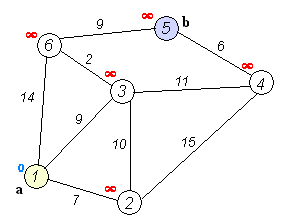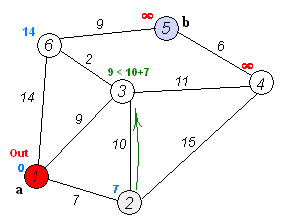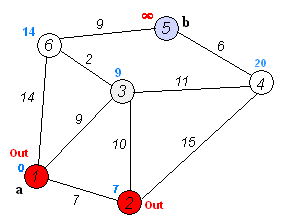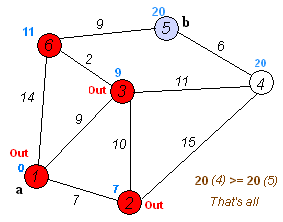
dij一个主要思路，将所有点分为两个集合S，T，初始集合S中只包含了起点，T集合包含所有点，要做的就是从T集合中不断选取与S集合中的点距离最短的并且未被加入S集合中的点，将这个点加入S集合，并用这个点去更新所有与这个点相邻的点，重复操作直到所有点都被加入S集合中。下面看一下dij的过程：

dij算法步骤：

dij动态图展示a到b最短路：

普通dij代码：

//时间复杂度O(n*n),
//空间复杂度O(n*n)，采用邻接矩阵存图，若采用邻接表则为(nlogn)
//关于邻接表邻接矩阵使用：
//讲述前先看这，假设一个图点有n个，边有m条，当n>mlogm时为稀疏图，反之为稠密图
//而邻接表适合于稀疏图，邻接矩阵适合稠密图
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int INF=0x3f3f3f3f;//无穷大
int edge[maxn][maxn];//邻接矩阵存边
bool vis[maxn];//标记点是否访问
int dis[maxn];//记录起点到终点的最短路
int n,m;
void init()
{for(int i=1;i<=n;i++){dis[i]=INF;vis[i]=false;}for(int i=0;i<=n;i++){for(int j=0;j<=n;j++){if(i==j) edge[i][j]=0;//自己到自己else     edge[i][j]=INF;//}}
}
void dij(int st)
{int pos;dis[st]=0;for(int i=1;i<n;i++)//进行n-1次操作{int len=INF;for(int j=1;j<=n;j++){if(!vis[j]&&dis[j]<len)//从未加入点中选一个与当前集合中的点路径最短的边{pos=j;len=dis[j];}}if(dis[pos]==INF) break;//没有可选的点了则提前退出vis[pos]=true;//将选出的点加入集合for(int j=1;j<=n;j++)//松弛与该点相邻的所有点{if(dis[pos]+edge[pos][j]<dis[j])//松弛操作，这里对比prim进行理解以区分prim和dij{dis[j]=dis[pos]+edge[pos][j];}}}
}
int main()
{while(scanf("%d%d",&n,&m)!=EOF){init();for(int i=1;i<=m;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);if(u!=v) edge[u][v]=edge[v][u]=w;}int st,en;scanf("%d%d",&st,&en);dij(st);printf("%d\n",dis[en]);}return 0;
}
/*
6 8
1 2 1
1 3 10
2 4 4
3 5 6
4 6 10
5 6 6
2 5 7
3 4 5
1 6
ans=14
*/

堆优化dij，思路和普通dij是一样的，主要是采用堆这种数据结构优化顶点出队顺序。

使用邻接矩阵实现的dijkstra算法的复杂度是O(V²)。使用邻接表的话，更新最短距离只需要访问每条边一次即可，因此这部分的复杂度是O(E).但是每次要枚举所有的顶点来查找下一个使用的顶点，因此最终复杂度还是O(V²)。在|E|比较小时，大部分的时间都花在了查找下一个使用的顶点上，因此需要使用合适的数据结构进行优化。

需要优化的是数值的插入(更新)和取出最小值两个操作，因此使用堆就可以了。把每个顶点当前的最短距离用堆来维护，在更新最短距离时，把对应的元素往根的方向移动以满足堆的性质。而每次从堆中取出的最小值就是下一次要用的顶点。这样堆中的元素共有O(V)个，更新和取出的操作有O(E)次，因此整个算法的复杂度是O(ElogV)。
堆主要使用C++ STL的priority_queue实现。在每次更新时往堆里插入当前最短距离和顶点的值对。插入的次数是O(E)次，当取出的最小值不是最短距离的话，就丢弃这个值。这样整个算法也可以在同样的时间内完成。

代码：

//时间复杂度O(nlogn),空间复杂度O(mlogm)
#include<bits/stdc++.h>
using namespace std;
const int maxn=105;
const int INF=0x3f3f3f3f;
typedef long long LL;
struct edge
{int en,len,next;
}E[maxn*maxn];
struct node
{int id,len;node(int id1=0,int len1=0)//C++构造点的编号和边长度{id=id1;len=len1;}friend bool operator<(node x,node y)//优先队列(堆)自定义优先级{return x.len>y.len;}
};
int head[maxn],num;
int n,m;
int vis[maxn],dis[maxn];
void init()
{memset(head,-1,sizeof(head));num=0;
}
void add(int st,int en,int len)
{E[num].en=en;E[num].len=len;E[num].next=head[st];head[st]=num++;
}
void dij(int st)
{for(int i=1;i<=n;i++){vis[i]=0;dis[i]=INF;}dis[st]=0;priority_queue<node>q;q.push(node(st,0));while(!q.empty()){node now=q.top();q.pop();if(vis[now.id]==1) continue;vis[now.id]=1;for(int i=head[now.id];i!=-1;i=E[i].next){int en=E[i].en;int len=E[i].len;if(!vis[en]&&(dis[en]>dis[now.id]+len)){dis[en]=dis[now.id]+len;q.push(node(en,dis[en]));}}}
}
int main()
{while(scanf("%d%d",&n,&m)!=EOF){if(n==0&&m==0) break;init();for(int i=1;i<=m;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);add(u,v,w);add(v,u,w);}int st,en;scanf("%d%d",&st,&en);dij(st);printf("%d\n",dis[en]);}return 0;
}
/*
测试数据：
6 8
1 2 1
1 3 10
2 4 4
3 5 6
4 6 10
5 6 6
2 5 7
3 4 5
1 6
ans=14
*/

整个图最短路详细版：

/*描述:求图中所有任意两点最短路的最大值、中位数、平均值*/
/*思路：采用堆优化的dij，普通dij一个主要思路，将所有点分为两个集合S，T，
初始集合S中只包含了起点，T集合包含所有点，要做的就是从T集合中不断选
取与S集合中的点距离最短的并且未被加入S集合中的点，将这个点加入S集合，
并用这个点去更新所有与这个点相邻的点，重复操作直到所有点都被加入S集合中。
堆优化dij采用堆这种数据结构优化出队顺序，因此时间复杂度较普通dij由n^2降低为nlogn*/
//算法时间复杂度O(n^2logn),空间复杂度O(m^2)
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int INF=0x3f3f3f3f;
typedef long long LL;
struct edge
{int en,len,next;
}E[maxn*maxn];
struct node
{int id,len;node(int id1=0,int len1=0)//C++构造点的编号和边长度{id=id1;len=len1;}friend bool operator<(node x,node y)//优先队列(堆)自定义优先级{return x.len>y.len;}
};
int head[maxn],num;
int n,m;
int vis[maxn],dis[maxn];
int ans[maxn];
int pre[maxn];
int path[maxn];
void init()
{memset(ans,0,sizeof(ans));memset(head,-1,sizeof(head));memset(path,-1,sizeof(path));num=0;
}
void add(int st,int en,int len)
{E[num].en=en;E[num].len=len;E[num].next=head[st];head[st]=num++;
}
void dij(int st)
{for(int i=1;i<=n;i++){vis[i]=0;dis[i]=INF;}dis[st]=0;pre[st]=-1;priority_queue<node>q;q.push(node(st,0));while(!q.empty()){node now=q.top();q.pop();if(vis[now.id]==1) continue;vis[now.id]=1;for(int i=head[now.id];i!=-1;i=E[i].next){int en=E[i].en;int len=E[i].len;if(!vis[en]&&(dis[en]>dis[now.id]+len)){pre[en]=now.id;dis[en]=dis[now.id]+len;q.push(node(en,dis[en]));}}}
}
int cnt1=0;
void print(int x)
{if(pre[x]==-1) return;print(pre[x]);path[++cnt1]=x;
}
int main()
{while(scanf("%d%d",&n,&m)!=EOF)//n个点m条边{if(n==0&&m==0) break;init();for(int i=1;i<=m;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);add(u,v,w);//无向图，因此构造两遍add(v,u,w);}int cnt=0;int sum=0;for(int i=1;i<n;i++)//枚举起点{dij(i);for(int j=i+1;j<=n;j++)//枚举终点{ans[++cnt]=dis[j];//存储i点到j点的最短路sum+=dis[j];}}//sort(ans+1,ans+1+cnt);for(int i=1;i<=cnt;i++){cout<<ans[i]<<" ";}cout<<endl;sort(ans+1,ans+1+cnt);printf("图中任意两点最短路最大值为：%d\n",ans[cnt]);printf("图中任意两点最短路平均值为：%.2f\n",(sum*1.0)/cnt);if(cnt&1)//奇数最短路点对中位数{printf("图中任意两点最短路的中位数为：%d\n",ans[cnt/2+1]);}else{printf("图中任意两点最短路的中位数为：%.2f\n",(ans[cnt/2+1]+ans[cnt/2])/2.0);}for(int i=1;i<n;i++){cnt1=0;path[++cnt1]=i;dij(i);for(int j=i+1;j<=n;j++){print(j);if(dis[j]==INF){printf("%d到%d之间不可达\n",i,j);continue;}printf("%d到%d得最短路径为:",i,j);for(int k=1;k<=cnt1;k++){if(k<cnt1) cout<<path[k]<<"-->";else cout<<path[k]<<endl;}cout<<"最短路值为:"<<dis[j]<<endl;cnt1=1;}}}return 0;
}
/*
测试数据：
6 8
1 2 1
1 3 10
2 4 4
3 5 6
4 6 10
5 6 6
2 5 7
3 4 5
*/

关于dij和floyd算法思想以及详细算法步骤参见这位博主：dij算法和floyd算法