统计学(第6版) 贾俊平读书笔记

第9章分类数据分析

9.1 分类数据与χ²统计量

统计数据的类型有分类数据、顺序数据和数值型数据。分类数据是对事物进行分类的结果。例如在泰坦尼克号海难的例子中，船上共2208人，其中男性1738人，女性470人。这里，性别是分类变量，有两个类别：男性和女性，男性和女性的人数都是事件结果，以频数的方式表现。χ²检验是对分类数据的频数进行分析的统计方法。

χ²可以用于测定两个分类变量之间的相关程度。若用f_o表示观察值频数，用f_e表示期望值频数，则χ²统计量可以写为：
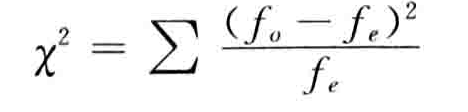
在这里插入图片描述
χ²统计量有如下特征：首先，χ² ≥ 0，因为它是对平房结果的汇总；其次，χ²统计量的分布与自由度有关；最后，χ²统计量描述了观察值与期望值的接近程度。两者越接近，计算出的χ²越小。χ²检验真是通过对χ²的计算结果与χ²分布中的临界值进行比较，做出是否拒绝原假设的统计决策。
卡方分布形状与自由度的关系
自由度越小，分布就越向左倾斜，随着自由度的增加，χ²分布的倾斜程度趋于缓解，χ²分布将趋近于对称的正态分布。利用χ²统计量，可以对分类数据进行拟合优度检验和独立性检验。

9.2 拟合优度检验

拟合优度检验是根据总体分布状况，计算出分类变量中各类别的期望频数，与分布的观察频数进行对比，判断期望频数与观察频数是否有显著差异，从而达到对分类变量进行分析的目的。

例题：
1912年4月15日，豪华巨轮泰坦尼克号与冰山相撞沉没。当时船上共有2208人，其中男性1738人，女性470人。海难发生后，幸存者共718人，其中男性374人，女性344人，以α = 0.1的显著水平检验存活状况与性别是否有关。
解：在本例中需要判断观察频数与期望频数是否一致。
H₀：观察频数与期望频数一致
H₁：观察频数与期望频数不一致
根据卡方检验公式进行计算：

f_o1 = 374，f_e1 = 1738*(718/2208) = 565
(f_o1 - f_e1)²/f_e1 = 64.6
f_o2 = 344，f_e2 = 470*(718/2208) = 153
(f_o2 - f_e2)²/f_e2 = 238.4
χ² = ∑ (f_o - f_e)²/f_e = 303

自由度计算公式为df = R - 1，R为分类变量的个数。df = 2-1=1，经查 χ²分布表， χ_0.1²(1) = 2.706，括号中的数字表示自由度。因为 χ²远大于χ_0.1²，故拒绝H₀，接受H₁，说明存活状况与性别显著相关。

9.3 列联分析：独立性检验

拟合优度检验是对一个分类变量的检验有时我们会遇到两个以上分类变量的问题。对于两个分类变量的分析，称为独立性检验，分析过程可以通过列联表的方式呈现。

列联表是由两个以上的变量进行交叉分类的频数分布表。由于列联表中的每个变量都可以有两个以上的类别，可以将横向变量（行）的划分类别视为R，纵向变量（列）的划分类别视为C，则可以把每一个具体的列联表称为R*C列联表。

独立性检验就是分析列联表中行变量和列变量是否相互独立。
在独立性检验中，可以采用下式计算任何一个单元中频数的期望值：
f_e = ( RT / n ) * ( CT / n ) * n = RT * CT / n
式中，f_e为给定单元中的频数期望值；RT为给定单元所在行的合计，CT为给定单元所在列的合计；n为观察值的总个数，即样本量。 χ²计算公式同9.1。 χ²的自由度 = (R - 1) * (C - 1)

9.4 列联表中的相关测量

φ相关系数是描述2*2列联表数据相关程度最常用的一种相关系数。它的计算公式为：

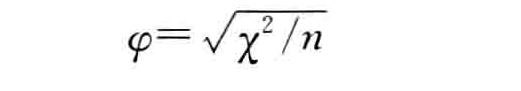
式中，χ²是按卡方公式计算出的值，n为列联表中的总频数，也即样本量。计算出的φ系数可以控制在0~1这个范围。

列相关系数又称列联系数，简称c系数，主要用于大于22列联表的情况。c系数的计算公式为：

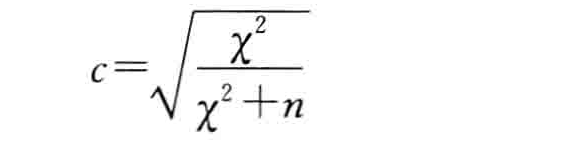
当列联表中的两个变量相互独立时，系数c = 0，但它不可能大于1。c系数的特点是，其可能的最大值依赖于列联表的行数和列数，且随着R和C的增大而增大。
V相关系数
克莱默提出了V相关系数，其计算公式为：

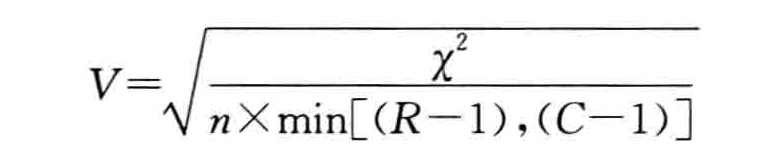
它的计算也是以χ*²值为基础，式中的min[(R-1),(C-1)]表示取(R-1)，(C-1)中较小的一个。当两个变量完全相关时，V=1；当两个变量相互独立时，V=0。

分析原料的质量是否与生产地有关，将500件随机抽取的产品按质量和产地构造列联表如下：

f_e = ( RT / n ) * ( CT / n ) * n = RT * CT / n
χ² = ∑ (f_o - f_e)²/f_e = 19.82
n = 500, min[(R-1),(C-1)] = 3-1=2
φ = sqrt(19.82/500) = 0.199
c = sqrt(19.82/(19.82+500)) = 0.195
V = sqrt(19.82/(500*2)) = 0.141
三种列联表系数的值都较小，因此综合起来可以认为，虽然检验表明原料的等级和地区有一定关系，但这种关系的密切程度不太高。

用χ²分布进行独立性检验，要求样本量必须足够大，特别是每个单元中的期望频数不能过小，否则会造成对χ²的高估，从而导致不适当地拒绝H₀的结论，处理的方法是将较小的f_e合并。

第10章方差分析

方差分析就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否具有显著影响。
在方差分析中，所要检验的对象称为因素或因子。因素的不同表现称为水平或处理。每个因子水平下得到的样本数据称为观测值。

进行方差分析时，需要考虑数据误差的来源。数据的误差是用平方和来表示的。反映全部数据误差大小的平方和称为总平方和(SST)，它反映了全部观测值的离散状况；反映组内误差大小的平方和称为组内平方和(SSE)，也称为误差平方和或残差平方和，它反映了每个样本内各观测值的离散状况；反映组间误差大小的平方和称为组间平方和(SSA)，它反映了样本均值之间的差异程度。

方差分析步骤

提出假设
在方差分析中，原假设所描述的是按照自变量的取值分成的类中，因变量的均值相等。因此，检验因素的k个水平（总体）的均值是否相等，需提出如下形式的假设：
H₀：μ₁ = μ₂ = … = μ_k 自变量对因变量没有显著影响
H₁：μ_i不全相等( i = 1，2，…，k ) 自变量对因变量有显著影响
构造检验的统计量
(1) 计算各样本的均值
(2) 计算全部观测值的总均值
(3) 计算各误差平方和

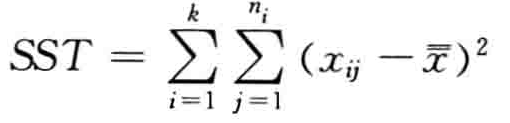
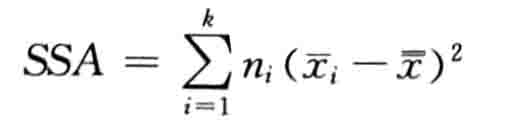
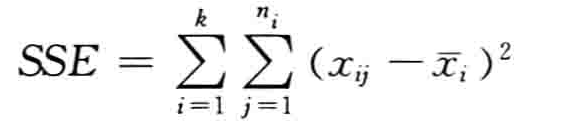
(4) 计算统计量
由于各误差平方和的大小与观测值的多少有关，为了消除观测值多少对误差平方和大小的影响，需要将其平均，也就是用各平方和除以它们所对应的自由度，这一结果称为均方。三个平方和所对应的自由度分别为：
SST的自由度为n-1，其中n为全部观测值的个数；
SSA的自由度为k-1，其中k为因素水平（总体）的个数；
SSE的自由度为n-k。
SSA的均方也称为组间均方或组间方差，记为MSA：MSA = SSA / ( k-1 )
SSE的均方也称为组内均方或组内方差，记为MSE：MSE = SSE / ( n-k )
将上述MSA和MSE进行对比，即得到所需要的检验统计量F。当H₀为真时，二者的比值服从分子自由度为k-1、分母自由度为n-k的F分布，即：
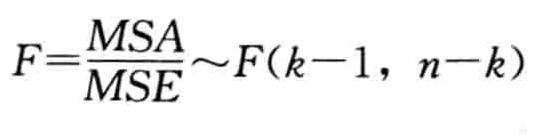
统计决策
将统计量的值F与给定的显著性水平α的临界值F_α进行比较，在F分布表中查找与分子自由度df₁ = k - 1、分母自由度df₂ = n - k相应的临界值 F_α(df₁, df₂)。
若F > F_α，则拒绝原假设H₀，表明各组均值之间的差异是显著的；若F < F_α，则不拒绝原假设。