Linux KSM共享内存

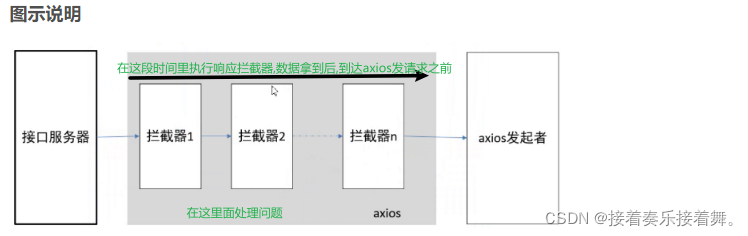
简介：作为一个系统管理程序（hypervisor），Linux® 有几个创新，2.6.32 内核中一个有趣的变化是 KSM(Kernel Samepage Merging) 允许这个系统管理程序通过合并内存页面来增加并发虚拟机的数量。本文探索 KSM 背后的理念（比如存储去耦合）、KSM 的实现、以及如何管理 KSM。

服务器虚拟化

虚拟化技术从上世纪 60 年代开始出现，经由 IBM® System/360® 大型机得以流行。50 年过后，虚拟化技术取得了跨越式发展，使得多个操作系统和应用程序共享一个服务器成为可能。这一特殊用途（称为服务器虚拟化）正在演变为数据中心，因为单个物理机能够用于托管 10 个（一般情况）或更多虚拟机（VM），如图 1 所示。这种虚拟化使基础设施更动态、更省电、（因而也）更经济。

图 1. 通过虚拟化进行的服务器合并

页面都是相同的。假如操作系统和应用程序代码以及常量数据在 VMs 之间相同，那么这个特点就很有用。当页面惟一时，它们可以被合并，从而释放内存，供其他应用程序使用。图 2 演示了内存共享，并展示了在内容相同的 VMs 之间共享页面时更多可用闲置内存的好处。

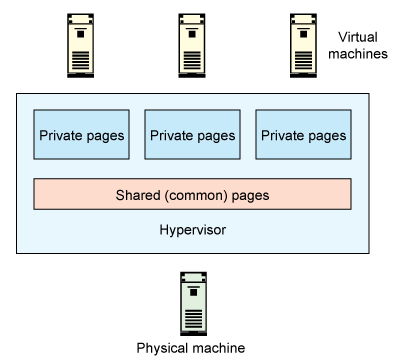
图 2. 跨 VMs 的内存共享

特性命名
本文描述的特性非常新；因此，其名称经历了一些变化。您将发现这个 Linux 内核特性称为 Kernel Shared Memory 或 Kernel Samepage Merging。

您很快就会发现，尽管 Linux 中的内存共享在虚拟环境中有优势（KSM 最初设计用于基于内核的虚拟机），但它在非虚拟环境中仍然有用。事实上，KSM 甚至在嵌入式 Linux 系统中也有用处，表明了这种方法的灵活性。下面，我们将探索这种 Linux 内存共享方法，以及如何使用该方法提高服务器的内存密度，从而增加其托管其他应用程序或 VMs 的能力。

其他技术支持

存储技术中的一个称为去耦合（de-duplication）的最新进展是 Linux 和其他系统管理程序中的内存共享的先驱。去耦合这种技术通过删除冗余数据（基于数据块，或者基于更大的数据片段，比如文件）来减少已存储的数据。公共数据片段被合并（以一种 copy-on-write [CoW] 方式），释放空间供其他用途。使用这种方法，存储成本更低，最终需要的存储器也更少。鉴于当前的数据增长速度，这个功能显得非常重要。

KSM 操作

KSM 作为内核中的守护进程（称为 ksmd）存在，它定期执行页面扫描，识别副本页面并合并副本，释放这些页面以供它用。KSM 执行上述操作的过程对用户透明。例如，副本页面被合并（然后被标记为只读），但是，如果这个页面的其中一个用户由于某种原因更改该页面，该用户将（以 CoW 方式）收到自己的副本。可以在内核源代码 ./mm/ksm.c 中找到 KSM 内核模块的完整实现。

KSM 依赖高级应用程序来提供指导，根据该指导确定合并的候选内存区域。尽管 KSM 可以只扫描系统中的匿名页面，但这将浪费 CPU 和内存资源（考虑到管理页面合并进程所需的空间）。因此，应用程序可以注册可能包含副本页面的虚拟区域。

KSM 应用程序编程接口（API）通过 madvise 系统调用（见清单 1）和一个新的建议参数（advice parameter）MADV_MERGEABLE（表明已定义的区域可以合并）来实现。可以通过 MADV_UNMERGEABLE 参数（立即从一个区域取消合并任何已合并页面）从可合并状态删除一个区域。注意，通过 madvise 来删除一个页面区域可能会导致一个 EAGAIN 错误，因为该操作可能会在取消合并过程中耗尽内存，从而可能会导致更大的麻烦（内存不足情况）。

清单 1. madvise 系统调用

#include <sys/mman.h>

int madvise( void *start, size_t length, int advice );

一旦某个区域被定义为 “可合并”，KSM 将把该区域添加到它的工作内存列表。启用 KSM 时，它将搜索相同的页面，以写保护的 CoW 方式保留一个页面，释放另一个页面以供它用。

KSM 使用的方法与内存去耦合中使用的方法不同。在传统的去耦合中，对象被散列化，然后使用散列值进行初始相似性检查。当散列值一致时，下一步是进行一个实际对象比较（本例中是一个内存比较），以便正式确定这些对象是否一致。KSM 在它的第一个实现中采用这种方法，但后来开发了一种更直观的方法来简化它。

在当前的 KSM 中，页面通过两个 “红-黑” 树管理，其中一个 “红-黑” 树是临时的。第一个树称为不稳定树，用于存储还不能理解为稳定的新页面。换句话说，作为合并候选对象的页面（在一段时间内没有变化）存储在这个不稳定树中。不稳定树中的页面不是写保护的。第二个树称为稳定树，存储那些已经发现是稳定的且通过 KSM 合并的页面。为确定一个页面是否是稳定页面，KSM 使用了一个简单的 32 位校验和（checksum）。当一个页面被扫描时，它的校验和被计算且与该页面存储在一起。在一次后续扫描中，如果新计算的校验和不等于此前计算的校验和，则该页面正在更改，因此不是一个合格的合并候选对象。

使用 KSM 进程处理一个单一的页面时，第一步是检查是否能够在稳定树中发现该页面。搜索稳定树的过程很有趣，因为每个页面都被视为一个非常大的数字（页面的内容）。一个 memcmp（内存比较）操作将在该页面和相关节点的页面上执行。如果 memcmp 返回 0，则页面相同，发现一个匹配值。反之，如果 memcmp 返回 -1，则表示候选页面小于当前节点的页面；如果返回 1，则表示候选页面大于当前节点的页面。尽管比较 4KB 的页面似乎是相当重量级的比较，但是在多数情况下，一旦发现一个差异，memcmp 将提前结束。请参见图 3 查看这个过程的视觉呈现。

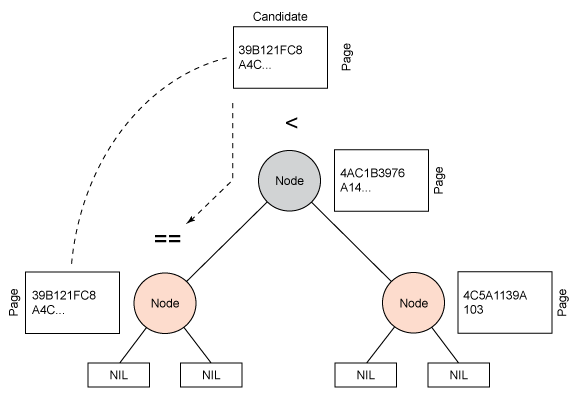
图 3. 搜索树中的页面的搜索过程

如果候选页面位于稳定树中，则该页面被合并，候选页面被释放。有关代码位于 ksm.c/stable_tree_search()（称为 ksm.c/cmp_and_merge_page()）中。反之，如果没有发现候选页面，则应转到不稳定树（参见 ksm.c/unstable_tree_search()）。

在不稳定树中搜索时，第一步是重新计算页面上的校验和。如果该值与原始校验和不同，则本次扫描的后续搜索将抛弃这个页面（因为它更改了，不值得跟踪）。如果校验和没有更改，则会搜索不稳定树以寻找候选页面。不稳定树的处理与稳定树的处理有一些不同。第一，如果搜索代码没有在不稳定树中发现页面，则在不稳定树中为该页面添加一个新节点。但是如果在不稳定树中发现了页面，则合并该页面，然后将该节点迁移到稳定树中。

当扫描完成（通过 ksm.c/ksm_do_scan() 执行）时，稳定树被保存下来，但不稳定树则被删除并在下一次扫描时重新构建。这个过程大大简化了工作，因为不稳定树的组织方式可以根据页面的变化而变化（还记得不稳定树中的页面不是写保护的吗？）。由于稳定树中的所有页面都是写保护的，因此当一个页面试图被写入时将生成一个页面故障，从而允许 CoW 进程为写入程序取消页面合并（请参见 ksm.c/break_cow()）。稳定树中的孤立页面将在稍后被删除（除非该页面的两个或更多用户存在，表明该页面还在被共享）。

如前所述，KSM 使用 “红-黑” 树来管理页面，以支持快速查询。实际上，Linux 包含了一些 “红-黑” 树作为一个可重用的数据结构，可以广泛使用它们。“红-黑” 树还可以被 Completely Fair Scheduler (CFS) 使用，以便按时间顺序存储任务。您可以在 ./lib/rbtree.c 中找到 “红-黑” 树的这个实现。

KSM 配置和监控

KSM 的管理和监控通过 sysfs（位于根 /sys/kernel/mm/ksm）执行。在这个 sysfs 子目录中，您将发现一些文件，有些用于控制，其他的用于监控。

第一个文件 run 用于启用和禁用 KSM 的页面合并。默认情况下，KSM 被禁用（0），但可以通过将一个 1 写入这个文件来启用 KSM 守护进程（例如，echo 1 > sys/kernel/mm/ksm/run）。通过写入一个 0，可以从运行状态禁用这个守护进程（但是保留合并页面的当前集合）。另外，通过写入一个 2，可以从运行状态（1）停止 KSM 并请求取消合并所有合并页面。

KSM 运行时，可以通过 3 个参数（sysfs 中的文件）来控制它。sleep_millisecs 文件定义执行另一次页面扫描前 ksmd 休眠的毫秒数。max_kernel_pages 文件定义 ksmd 可以使用的最大页面数（默认值是可用内存的 25%，但可以写入一个 0 来指定为无限）。最后，pages_to_scan 文件定义一次给定扫描中可以扫描的页面数。任何用户都可以查看这些文件，但是用户必须拥有根权限才能修改它们。

还有 5 个通过 sysfs 导出的可监控文件（均为只读），它们表明 ksmd 的运行情况和效果。full_scans 文件表明已经执行的全区域扫描的次数。剩下的 4 个文件表明 KSM 的页面级统计数据：

•pages_shared：KSM 正在使用的不可交换的内核页面的数量。
•pages_sharing：一个内存存储指示。
•pages_unshared：为合并而重复检查的惟一页面的数量。
•pages_volatile：频繁改变的页面的数量。
KSM 作者定义：较高的 pages_sharing/pages_shared 比率表明高效的页面共享（反之则表明资源浪费）。

结束语

Linux 并不是使用页面共享来改进内存效率的惟一系统管理程序，但是它的独特之处在于将其实现为一个操作系统特性。VMware 的 ESX 服务器系统管理程序将这个特性命名为 Transparent Page Sharing (TPS)，而 XEN 将其称为 Memory CoW。不管采用哪种名称和实现，这个特性都提供了更好的内存利用率，从而允许操作系统（KVM 的系统管理程序）过量使用内存，支持更多的应用程序或 VM。您可以在最新的 2.6.32 Linux 内核中发现 KSM — 以及其他很多有趣的特性。