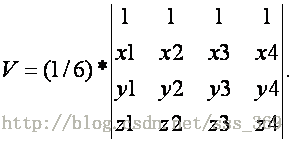当正四面体的棱长为a时,体积:√2a³/12,表面积√3a^2。
解答过程如下:

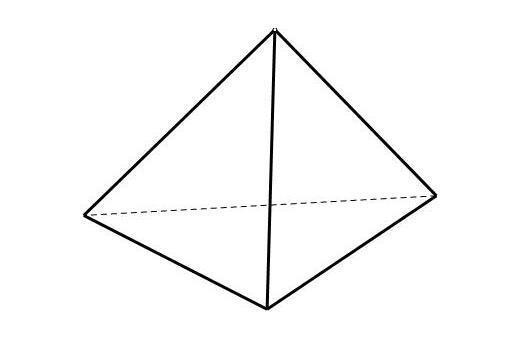
正四面体是由四个全等的正三角形所组成的几何体。它有四个面、四个顶点、六条棱。每个二面角均为70°32’,有四个三面角,每个三面角的面角均为60°,以a表示棱长,A表示全面积,V表示体积。
例如,表面积为8平方厘米的正四面体,体积约为1.1697立方米;表面积为8平方厘米的正六面体(正方体),体积约为1.539立方厘米;而表面积是8平方厘米的球,体积却约有2.128立方厘米。
扩展资料
常用结论
(1)与体积有关的几个结论。
①一个组合体的体积等于它的各部分体积的和或差。
②底面面积及高都相等的两个同类几何体的体积相等。
(2)几个与球有关的切、接常用结论。
a、正方体的棱长为a,球的半径为R,
①若球为正方体的外接球,则;2R=√3a
②若球为正方体的切球,则2R=a;
③若球与正方体的各棱相切,则2R=√2a。
b、正四面体的外接球与切球的半径之比为3:1.