层次分析法
层次分析法是笔者参加建模比赛最喜欢用的模型,也是各种算法中最简单的算法,大部分类型的题目都可以用层次分析法入手,进行初步的分析。
层次分析法的优点在于不需要任何数据,矩阵中用到的数据都是建模者主观上的比较,适用于没有数据或者数据少的问题中,缺点在于有些时候逻辑不够严谨以及模型较单一,推广能力差。
层次分析法概念:
层次分析法(AHP)特点在于对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。是对难以完全定量的复杂系统做出决策的模型和方法
- 注:决策是指面临多种方案时需要根据一定的标准选择某一种方案,如根据景区的景色、居住环境、餐饮特色、交通便利程度、旅游费用等来选择某一旅游目的地。
层次分析法原理:
根据问题的性质和要达到的总目标,将问题分解成不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
层次分析法步骤:
1、 建立层次结构模型
2、 构造成对比较矩阵
3、 层次单排序及其一致性检验
4、 层次总排序及其一致性检验
如何构建层次结构模型
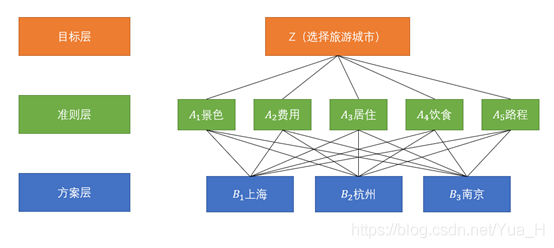
将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分为目标层、准则层、方案层,绘制出层次结构图
目标层:决策的目的,要解决的问题
准则层:考虑的因素、决策的准则
方案层:决策时的备选方案
如何构造成对比较矩阵
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因此提出一致矩阵法,即
(1)不把所有因素放在一起比较,而是两两相互比较
(2)对此时采用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,以提高准确度。
- 成对比较矩阵时表示本层所有因素针对上一层某一个因素的相对重要性的比较。成对比较矩阵的元素a_ij用1——9的标度方法给出。

如何一致性检验

计算一致性指标CI
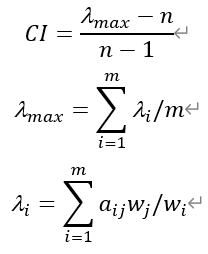

为了避免随机因素所造成的误差,还需将 CI 和随机一致性指标 RI 进行比较,得出检验系数 CR,当CR<0.1,该矩阵的一致性可以接受,若CR>=0.1,该矩阵的一致性不能接受。
公式如下:
CR=CI/RI
实例:
在上海,杭州,南京三个旅游目的地中选择一个最合适的城市进行旅游。
符号说明

步骤一:绘制层次结构模型
列举出影响游客选择旅游目的地的因素——景色,费用,居住,饮食,路程。
然后列出旅游的城市——上海,杭州,南京
确定目标层、准则层和方案层。
步骤二:构建成对比较矩阵
根据资料和实际数据,我们可以列出成对比较矩阵

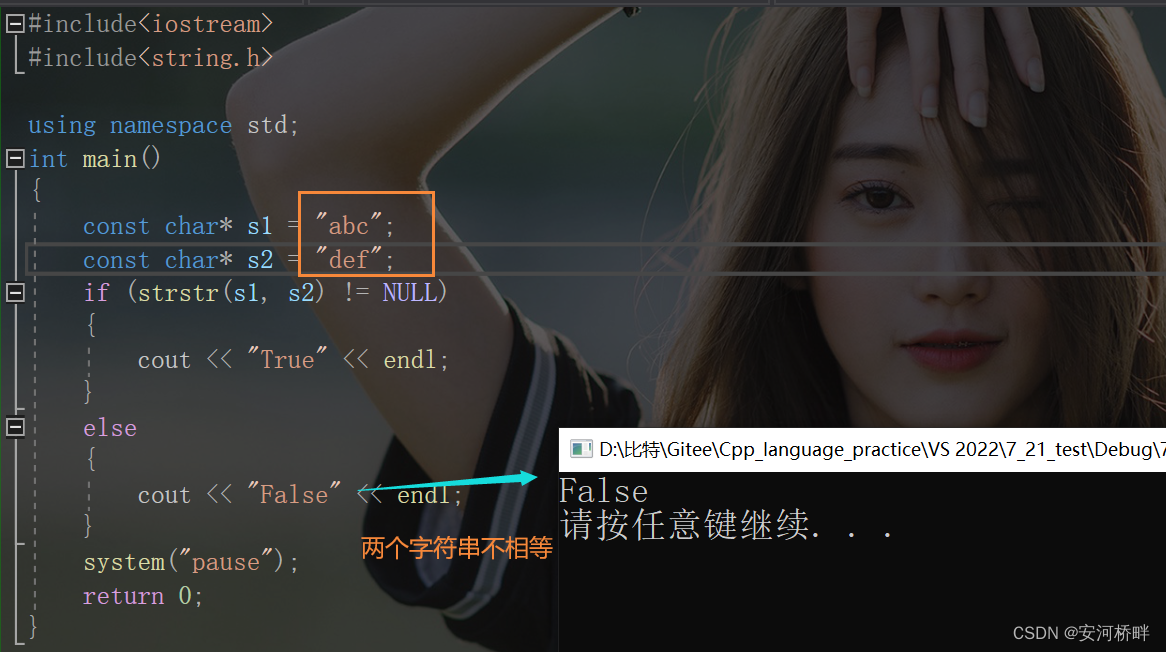
步骤三:一致性检验(代码见最后)
A矩阵的CI=0.0180,CR=0.0161,一致性检验通过
步骤四:得出结果
经过计算
A_1 A_2 A_3 A_4 A_5对Z的权重为【0.2636,0.4758,0.0538,0.0981,0.1087】
B_1 B_2 B_3对A_1的权重为【0.5954,0.2764,0.1283】
B_1 B_2 B_3对A_2的权重为【0.0819,0.2363,0.6817】
B_1 B_2 B_3对A_3的权重为【0.4286,0.4286,0.1429】
B_1 B_2 B_3对A_4的权重为【0.6337,0.1919,0.1744】
B_1 B_2 B_3对A_5的权重为【0.1667,0.1667,0.6667】
结论:
B_1 B_2 B_3对总目标的权重为【0.3,0.245,0.455】,因此选择南京作为旅游目的地最合适。
多属性决策
多属性决策模型实质:
利用已有的决策信息,通过一定的方式,对一组(有限个)备选方案进行排序或择优。
主要由两部分构成:(1)获取决策信息——一般包括属性权重和属性值(实数、区间数和语言),其中属性权重的确定是多属性决策中的一个重要研究内容;(2)通过一定方法对决策信息进行集结并对方案进行排序和择优。
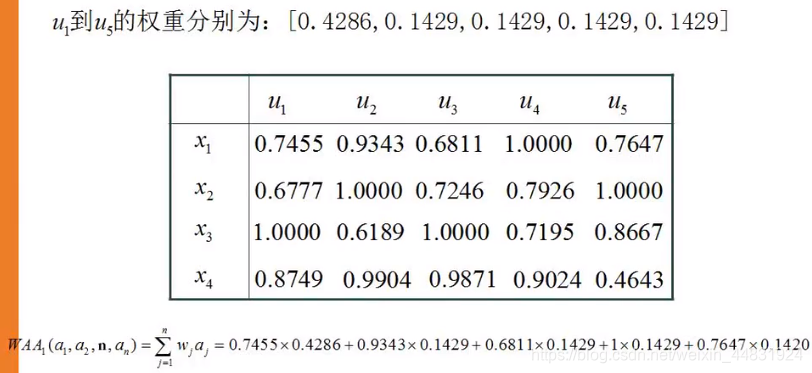
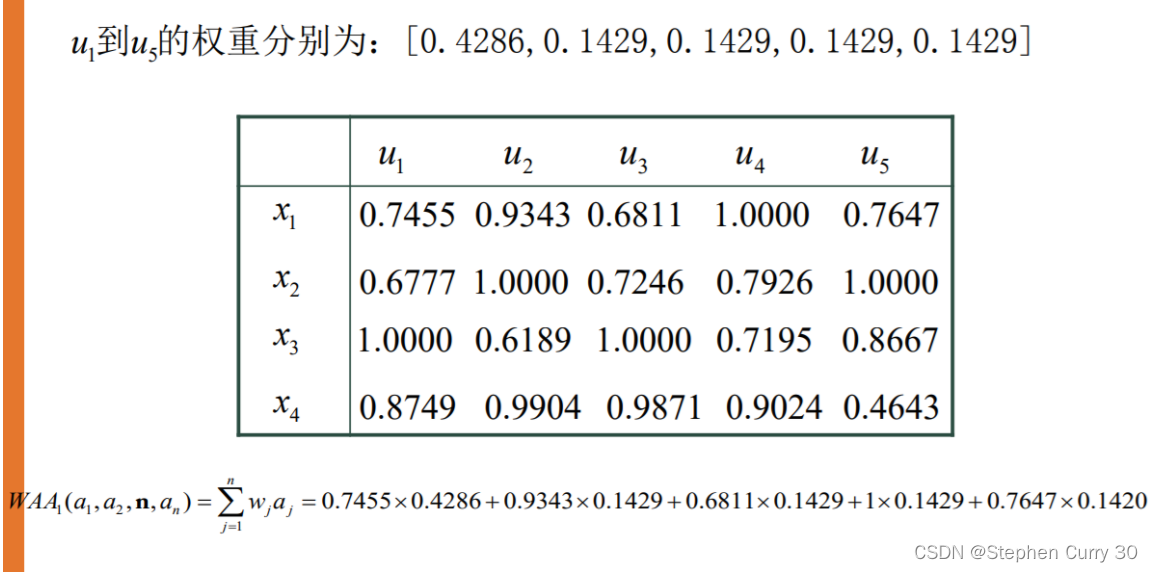
加权算数平均算子(WAA)
信息集结方法包括加权算数平均算子(WAA)、加权几何平均算子(WGA),有序加权平均算子(OWA),本文主要介绍WAA。
定义

属性归一化
属性类型一般有效益型、成本性、固定性、区间型、偏离区间型等。其中效益型属性是指属性值越大越好的属性;成本型属性是指属性值越小越好的属性;固定型属性是指属性值越接近某个固定值α_i越好的属性;区间型属性是指属性值越接近某个固定区间[〖q_1〗j,〖q_2〗j](包括落入该区间)越好的属性,偏离区间型属性是指属性值越偏离某个固定区间[〖q_1〗j,〖q_2〗j ]越好的属性。为了消除不同物理量纲对决策结果的影响,决策时可按下列公式对数据进行规范化处理。
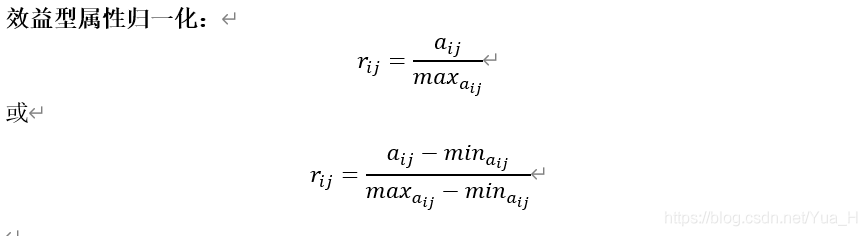


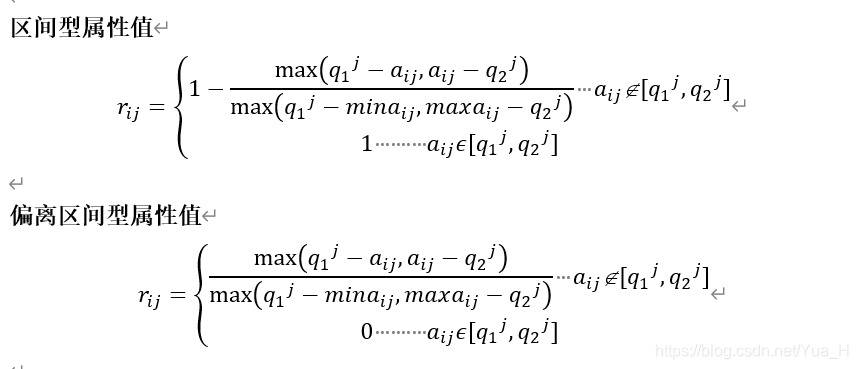
多属性决策实例:
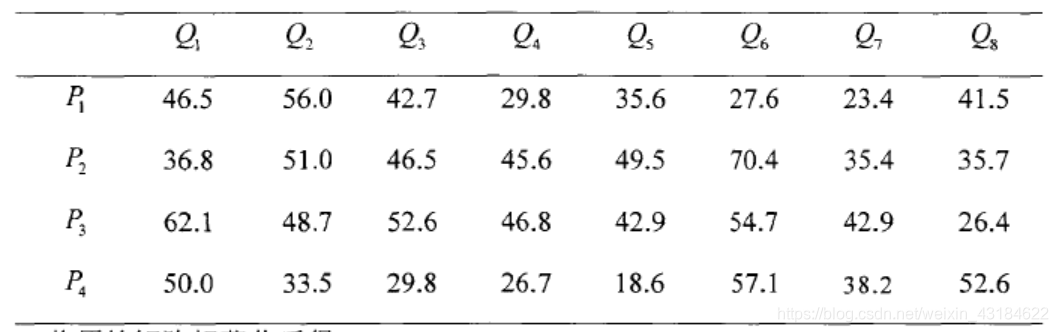
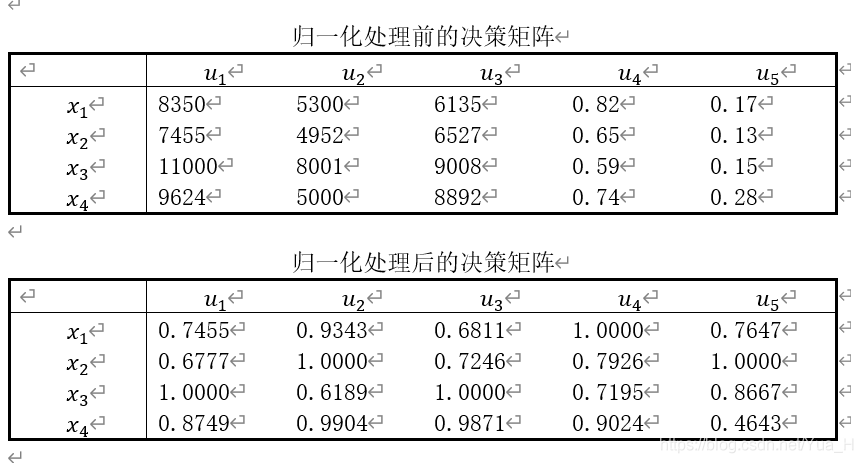
投资银行拟对四家企业(方案)进行投资,抽取下列5项指标(属性)进行评估——产值(万元);投资成本(万元);销售额(万元);国家收益比重;环境污染程度
投资银行考察了上年度4家企业的上述指标情况(其中污染程度系有环保部门历时检测并量化),所得结果如表所示。
在各项指标中,投资成本、环境污染程度为成本型,其他为效益型,属性权重信息完全未知,试确定最佳投资方案。
计算属性权重
对五个属性构建成对比较矩阵,计算属性权重

一致性检验的MATLAB代码
disp(' 请输入成对比较矩阵A ');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>pi=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);
% 以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
end