matlab---多属性决策模型
- 加权算术平均算子
- 属性值的归一化处理
- 多属性决策模型举例
多属性决策的实质是利用已有的决策信息通过一定的方式对一组(有限个)备选方案进行排序或择优。它主要由2部分组成:
-
获取决策信息。
决策信息一般包括两个方面的内容:属性权重和属性值(属性值主要有三种形式:实数、区间数和语言)。其中,属性权重的确定是多属性决策中的一个重要研究内容。 -
通过一定的方式对决策信息进行集结并对方案进行排序和择优。
加权算术平均算子

下面列举一例:
我校教学水平评估,在4项指标:办学指导思想,学分,教学效果,特色项目。得分为数据组(91,82,83,93),4项指标的权重向量为w=(0.4,0.1,0.2,0.3)^T。则加权平均综合得分为:
W A Aw(91,82,83,93)
=91 * 0.4 + 82 * 0.1 + 83 * 0.2 + 93 * 0.3
=89.1
注意: 量纲必须要统一,即属性值要归一化,如打分要么都以百分制,要么都以十分制。
那么怎么进行属性值的归一化,见下:
属性值的归一化处理
属性类型一般有效益型、成本型、固定性、偏离型、区间型、偏离区间型等,其中效益型属性是指属性值越大越好的属性,成本型属性是指属性值越小越好的属性,固定型属性是指属性值越接近某个固定值越好的属性,偏离型属性是指属性值越偏离某个固定值越好的属性。区间型属性是指属性值越接近某个固定区间(包括落在该区间)越好的属性,偏离区间型属性是指属性值越偏离某个固定区间越好的属性。为了消除不同物理量纲对决策结果的影响,决策时可按下列公式对数据进行规范化处理:
a_ij表示待处理的属性值
-
效益型

-
成本型

-
固定型
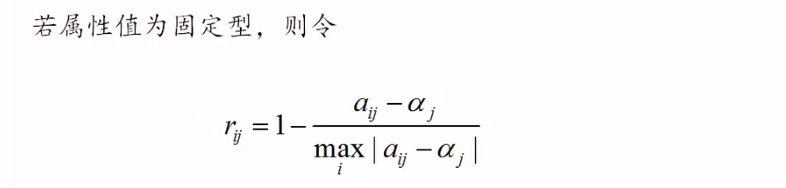
-
偏离型
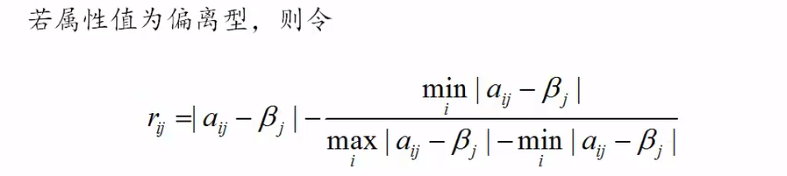
-
区间型

-
偏离区间型

多属性决策模型举例
用加权平均算子与属性归一化来做多属性决策
例:投资银行拟对某市4家企业(方案)进行投资,抽取下列5项指标(属性)进行评估:
产值(万元);投资成本(万元);销售额(万元);国家收益比重;环境污染程度。
投资银行考察了上半年4家企业的上述指标情况(其中污染程度系有环保部门历时检测并量化),所得评估结果如下表所示。在各项指标中,投资成本、环境污染程度为成本型,其他为效益型。属性权重信息完全未知,试确定最佳投资方案。

其中x分别表示4家企业,u表示5项指标。通过上面介绍的公式对各项指标(属性)进行归一化,得到归一化处理后的决策矩阵结果如下:

根据层次分析法,对5个属性构建成对比较矩阵:A =
[ 1, 3,3,3,3;
1/3,1,1,1,1;
1/3,1,1,1,1;
1/3,1,1,1,1;
1/3,1,1,1,1;]
-
在建立了层次分析模型和成对比较矩阵后,我们使用代码来实现权重的求解,代码见层次分析法。最后得到的结果为:
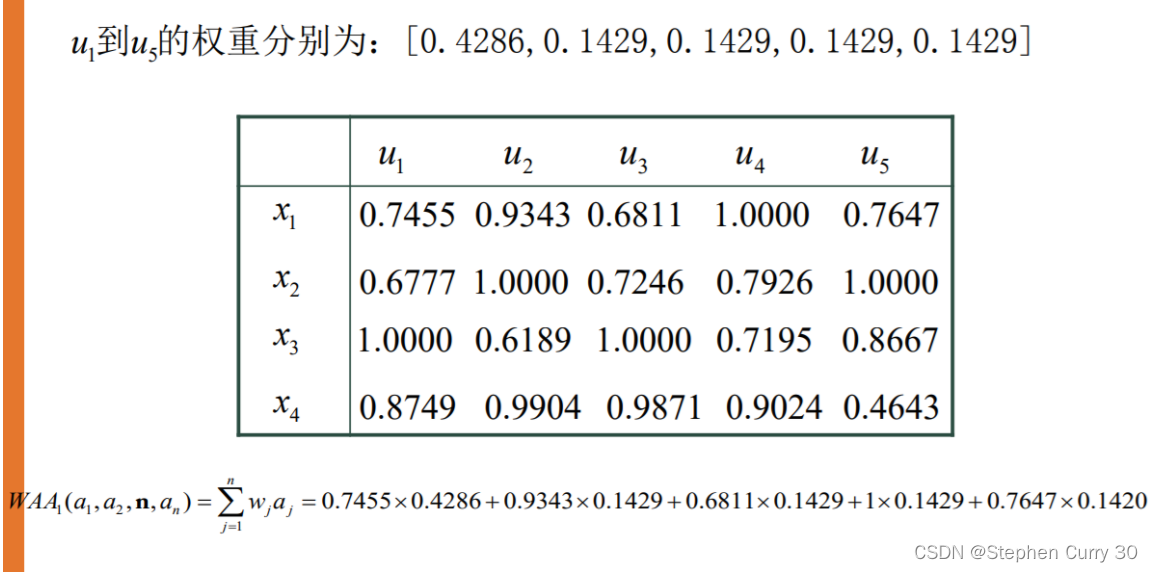
u1到u5的权重分别为:
[0.4286,0.1429,0.1429,0.1429,0.1429] -
由属性权重和属性值计算总得分:
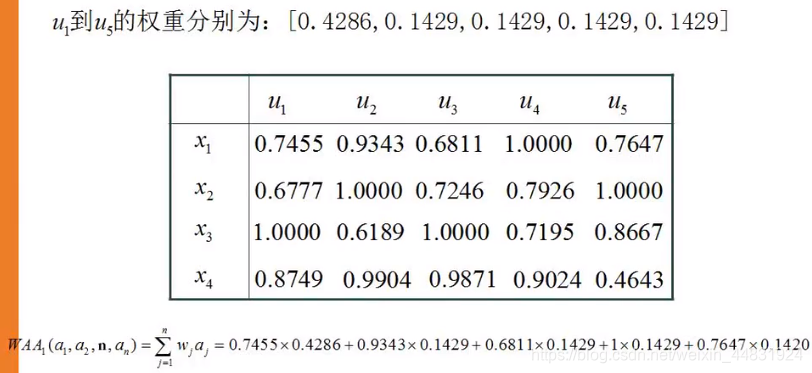
WAAw为加权算术平均算子,根据博客开头的公式分别求出X1,X2,X3,X4对应的WAA1,WAA2,WAA3,WAA4. -
最后做出决策:
由上面的计算结果得企业1-4得分分别为:0.80,0.79,0.89,0.85;所以应该投资企业3.