matlab实现决策矩阵规范化(多属性决策)
一般来说,不同的决策变量量纲也不同,规范化可以消除量纲对最终结果的影响,使不同变量具有可比性。
假设决策矩阵为 A = ( a i j ) m × n A=({a_{ij}})_{m×n} A=(aij)m×n, 规范化矩阵为 R = ( r i j ) m × n R=({r_{ij}})_{m×n} R=(rij)m×n, 对于效益性指标和成本型指标可以按下列公式转化。
首先, 对于同一属性,找出所有方案中这一指标值的最大值 a m a x a_{max} amax和最小值 a m i n a_{min} amin;
对于效益性指标(越大越好)
对于效益性指标,按照下列公式进行规范化处理:
r i j = ( a i j − a m i n ) / ( a m a x − a m i n ) r_{ij}=(a_{ij}-a_{min})/(a_{max}-a_{min}) rij=(aij−amin)/(amax−amin)
对于成本型指标(越小越好):
对于成本型指标,按照下列公式进行规范化处理:
r i j = ( a m a x − a i j ) / ( a m a x − a m i n ) r_{ij}=(a_{max}-a_{ij})/(a_{max}-a_{min}) rij=(amax−aij)/(amax−amin)
matlab 实现
如下图所示,P1、P2、P3、P4表示四个不同的方案,Q1~Q8为8个不同的指标,假设8个指标均为效益性矩阵。
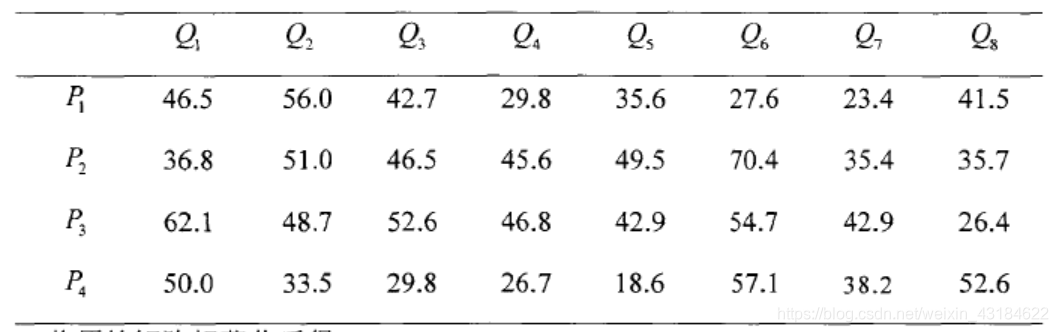
则决策矩阵可表示为:
A=[46.5 56.0 42.7 29.8 35.6 27.6 23.4 41.5;36.8 51.0 46.5 45.6 49.5 70.4 35.4 35.7;62.1 48.7 52.6 46.8 42.9 54.7 42.9 26.4;50.0 33.5 29.8 26.7 18.6 57.1 38.2 52.6];
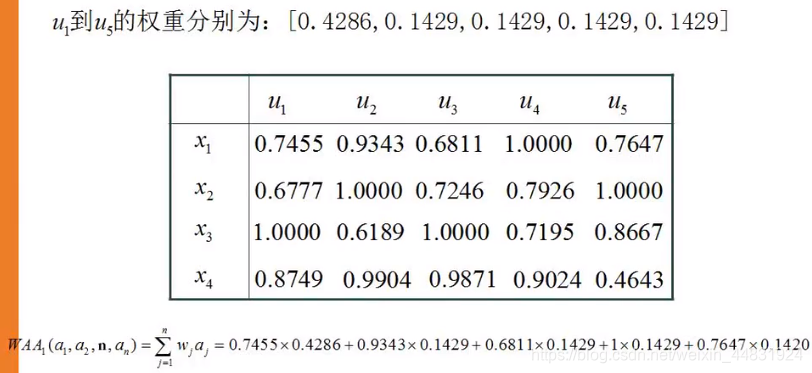
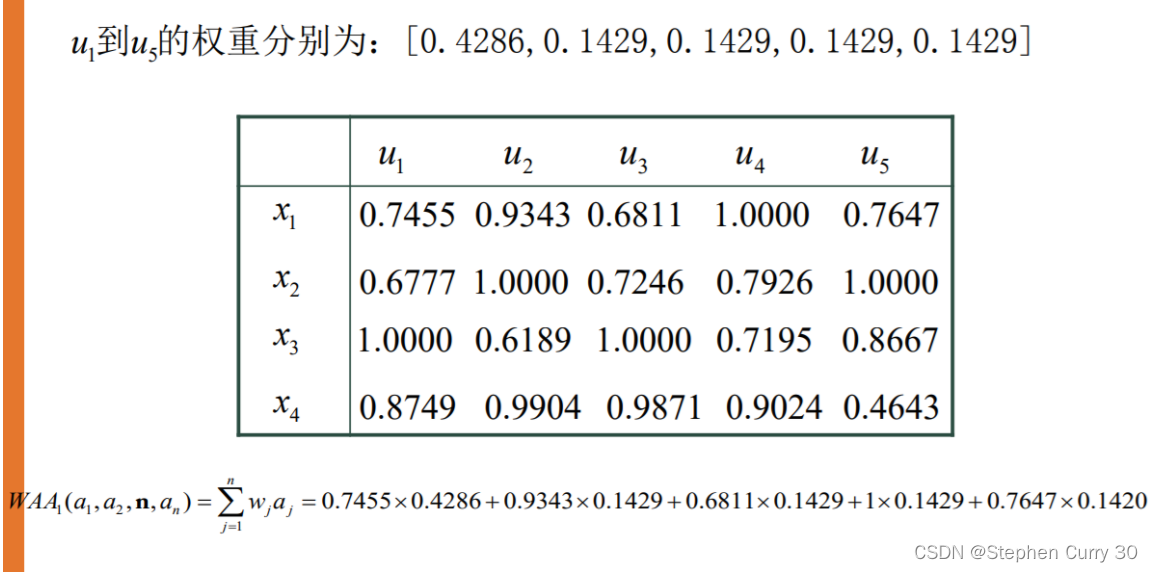
对于属性 Q 1 Q_1 Q1,四个方案中的最大值 a m a x , 1 = 62.1 a_{max ,1}=62.1 amax,1=62.1,最小值为 a m i n , 1 = 36.8 a_{min,1}=36.8 amin,1=36.8,则对于规范化矩阵
r 11 = ( a 11 − a m i n , 1 ) / ( a m a x , 1 − a m i n , 1 ) = 0.3834 r_{11}=(a_{11}-a_{min,1})/(a_{max,1}-a_{min,1})=0.3834 r11=(a11−amin,1)/(amax,1−amin,1)=0.3834
以此类推。
matlab代码如下:
A=[46.5 56.0 42.7 29.8 35.6 27.6 23.4 41.5;36.8 51.0 46.5 45.6 49.5 70.4 35.4 35.7;62.1 48.7 52.6 46.8 42.9 54.7 42.9 26.4;50.0 33.5 29.8 26.7 18.6 57.1 38.2 52.6];
min_a=min(A);%求每一列的最小值
max_a=max(A);
deta_a=max_a-min_a;
for i=1:size(A,1)for j=1:size(A,2)B(i,j)=(A(i,j)-min_a(j))/deta_a(j);end
end
对于其他类型的指标如区间型等,可参考https://blog.csdn.net/weixin_40108753/article/details/81222072
https://www.cnblogs.com/Qling/p/9295414.html