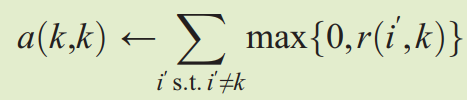论文题目:Clustering by Passing Messages Between Data Points
论文来源:Clustering by Passing Messages Between Data Points
翻译人:BDML@CQUT实验室
Clustering by Passing Messages Between Data Points
通过在数据点之间传递消息进行聚类
Abstract
Clustering data by identifying a subset of representative examples is important for processing sensory signals and detecting patterns in data. Such “exemplars” can be found by randomly choosing an initial subset of data points and then iteratively refining it, but this works well only if that initial choice is close to a good solution. We devised a method called “affinity propagation,” which takes as input measures of similarity between pairs of data points. Real-valued messages are exchanged between data points until a high-quality set of exemplars and corresponding clusters gradually emerges. We used affinity propagation to cluster images of faces, detect genes in microarray data, identify representative sentences in this manuscript, and identify cities that are efficiently accessed by airline travel. Affinity propagation found clusters with much lower error than other methods, and it did so in less than one-hundredth the amount of time.
摘要
通过识别代表性示例的子集来对数据进行聚类对于处理感官信号和检测数据中的模式非常重要。可以通过随机选择数据点的初始子集然后进行迭代细化来找到这样的“示例”,但这仅在初始选择接近于好的解决方案的情况下才有效。我们设计了一种称为“近邻传播聚类(AP聚类)”的方法,该方法将输入的数据点对之间的相似性作为输入度量。在数据点之间交换实值消息,直到逐渐出现高质量的示例集和相应的簇。我们使用AP聚类算法对人脸图像进行聚类,检测微阵列数据中的基因,确定该手稿中的代表性句子以及确定可通过航空旅行有效访问的城市。AP聚类算法发现群集的错误率比其他方法低得多,并且这样做的时间少于一百分之一。
正文
Clustering data based on a measure of similarity is a critical step in scientific data analysis and in engineering systems. A common approach is to use data to learn a set of centers such that the sum of squared errors between data points and their nearest centers is small. When the centers are selected from actual data points, they are called “exemplars.” The popular k-centers clustering technique*(1)* begins with an initial set of randomly selected exemplars and iteratively refines this set so as to decrease the sum of squared errors. k-centers clustering is quite sensitive to the initial selection of exemplars, so it is usually rerun many times with different initializations in an attempt to find a good solution. However, this works well only when the number of clusters is small and chances are good that at least one random initialization is close to a good solution. We take a quite different approach and introduce a method that simultaneously considers all data points as potential exemplars. By viewing each data point as a node in a network, we devised a method that recursively transmits real-valued messages along edges of the network until a good set of exemplars and corresponding clusters emerges. As described later, messages are updated on the basis of simple formulas that search for minima of an appropriately chosen energy function. At any point in time, the magnitude of each message reflects the current affinity that one data point has for choosing another data point as its exemplar, so we call our method “affinity propagation.” Figure 1A illustrates how clusters gradually emerge during the message-passing procedure.
基于相似性度量对数据进行聚类是科学数据分析和工程系统中的关键步骤。一种常见的方法是使用数据来学习一组中心,以使数据点与其最近的中心之间的平方误差之和很小。当从实际数据点中选择中心时,它们被称为“示例”。流行的k-中心聚类技术 (1) 从一组随机选择的样本的初始集合开始,然后迭代完善该集合,以减少平方误差之和。k-中心聚类算法对示例的初始选择非常敏感,因此通常使用不同的初始化将其重新运行很多次,以期找到一个好的解决方案。但是,这仅在簇数少且至少有一个随机初始化接近一个好的解决方案的机会很大时才有效。我们采用了一种完全不同的方法,并介绍了一种同时将所有数据点视为潜在示例的方法。通过将每个数据点视为网络中的一个节点,我们设计了一种方法,可以沿着网络的边缘递归传输实值消息,直到出现一组好的示例和相应的群集。如稍后所述,基于搜索适当选择的能量函数的最小值的简单公式来更新消息。在任何时间点,每条消息的大小都反映了一个数据点选择另一个数据点作为其示例的当前近邻传播,因此我们将我们的方法称为“近邻传播聚类”。图1A说明了在消息传递过程中群集如何逐渐出现。
Fig. 1. How affinity propagation works. (A) Affinity propagation is illustrated for two-dimensional data points, where negative Euclidean distance (squared error) was used to measure similarity. Each point is colored according to the current evidence that it is a cluster center (exemplar). The darkness of the arrow directed from point i i i to point k k k corresponds to the strength of the transmitted message that point i i i belongs to exemplar point k k k. (B) “Responsibilities” r ( i , k ) r(i,k) r(i,k) are sent from data points to candidate exemplars and indicate how strongly each data point favors the candidate exemplar over other candidate exemplars. © “Availabilities” a ( i , k ) a(i,k) a(i,k) are sent from candidate exemplars to data points and indicate to what degree each candidate exemplar is available as a cluster center for the data point. (D) The effect of the value of the input preference (common for all data points) on the number of identified exemplars (number of clusters) is shown. The value that was used in (A) is also shown, which was computed from the median of the pairwise similarities.
图1. AP聚类算法如何工作。**(A)**说明了二维数据点的AP聚类算法,其中使用负欧几里德距离(平方误差)来衡量相似度。根据当前证据表明每个点都是聚类中心(示例性),每个点都带有颜色。从点 i i i 指向点 k k k 的箭头的暗度对应于所传输消息的强度,即点 i i i 属于示例点 k k k 。 (B)“Responsibilities” r ( i , k ) r(i,k) r(i,k) 从数据点发送到候选样例,并指出每个数据点对候选样例的支持程度多于其他候选样例。 **(C)**从候选样本到数据点的“Availabilities” a ( i , k ) a(i,k) a(i,k) 的范围,并指示每个候选样本在何种程度上可用作数据点的聚类中心。 **(D)显示了输入首选项的值(所有数据点共有)对识别出的样本数(聚类数)的影响。还显示了在(A)**中使用的值,该值是从成对相似性的中位数计算得出的。
Affinity propagation takes as input a collection of real-valued similarities between data points, where the similarity s ( i , k ) s(i,k) s(i,k) indicates how well the data point with index k k k is suited to be the exemplar for data point i i i. When the goal is to minimize squared error, each similarity is set to a negative squared error (Euclidean distance): For points x i x_i xi and x k x_k xk , s ( i , k ) = − ∣ ∣ x i − x k ∣ ∣ 2 s(i,k) = −||x_i− x_k||^2 s(i,k)=−∣∣xi−xk∣∣2. Indeed, the method described here can be applied when the optimization criterion is much more general. Later, we describe tasks where similarities are derived for pairs of images, pairs of microarray measurements, pairs of English sentences, and pairs of cities. When an exemplar-dependent probability model is available, s ( i , k ) s(i,k) s(i,k) can be set to the log-likelihood of data point i i i given that its exemplar is point k k k. Alternatively, when appropriate, similarities may be set by hand.
AP聚类算法将数据点之间的实值相似性集合作为输入,其中相似性 s ( i , k ) s(i,k) s(i,k) 表示索引为 k k k 的数据点适合作为数据点 i i i 的示例的程度。当目标是最小化平方误差时,将每个相似度设置为负平方误差(欧式距离):对于点 x i x_i xi 和 x k x_k xk , s ( i , k ) = − ∣ ∣ x i − x k ∣ ∣ 2 s(i,k) = −||x_i− x_k||^2 s(i,k)=−∣∣xi−xk∣∣2 。实际上,当优化标准更为通用时,可以应用此处描述的方法。随后,我们将描述在这些任务中,从成对的图像、成对的微阵列测量、成对的英语句子和成对的城市中得出相似性。当依赖于样本的概率模型可用时,可以将 s ( i , k ) s(i,k) s(i,k) 设置为数据点 i i i 的对数似然,前提是其样本为点 k k k 。或者,在适当的时候,相似性可以手动设置。
Rather than requiring that the number of clusters be prespecified, affinity propagation takes as input a real number s ( k , k ) s(k,k) s(k,k) for each data point k so that data points with larger values of s ( k , k ) s(k,k) s(k,k) are more likely to be chosen as exemplars. These values are referred to as “preferences.” The number of identified exemplars (number of clusters) is influenced by the values of the input preferences, but also emerges from the message-passing procedure. If a priori, all data points are equally suitable as exemplars, the preferences should be set to a common value— this value can be varied to produce different numbers of clusters. The shared value could be the median of the input similarities (resulting in a moderate number of clusters) or their minimum (resulting in a small number of clusters).
相似性传播不是要求预先指定聚类的数目,而是将每个数据点 k k k 的实数 s ( k , k ) s(k,k) s(k,k) 作为输入,使得具有较大 s ( k , k ) s(k,k) s(k,k) 值的数据点更有可能被选为样本。这些值被称为“首选项”已识别样本的数量(聚类的数量)受输入偏好值的影响,但也来自消息传递过程。如果先验地,所有的数据点都同样适合作为样本,那么偏好应该被设置为一个共同的值——这个值可以变化以产生不同数量的聚类。共享值可以是输入相似性的中间值(产生中等数量的聚类)或它们的最小值(产生少量的聚类)。
There are two kinds of message exchanged between data points, and each takes into account a different kind of competition. Messages can be combined at any stage to decide which points are exemplars and, for every other point, which exemplar it belongs to. The “responsibility” r ( i , k ) r(i,k) r(i,k) , sent from data point i i i to candidate exemplar point k k k, reflects the accumulated evidence for how well-suited point k k k is to serve as the exemplar for point i i i, taking into account other potential exemplars for point i i i (Fig. 1B). The “availability” a ( i , k ) a(i,k) a(i,k) , sent from candidate exemplar point k k k to point i i i , reflects the accumulated evidence for how appropriate it would be for point i i i to choose point k k k as its exemplar, taking into account the support from other points that point k k k should be an exemplar (Fig. 1C). r ( i , k ) r(i,k) r(i,k) and a ( i , k ) a(i,k) a(i,k) can be viewed as log-probability ratios. To begin with, the availabilities are initialized to zero: a ( i , k ) = 0 a(i,k) = 0 a(i,k)=0 . Then, the responsibilities are computed using the rule
r ( i , k ) ← s ( i , k ) − max k ′ s . t . k ′ ≠ k { a ( i , k ′ ) + s ( i , k ′ ) } (1) r(i,k)\leftarrow s(i,k) - \max_{k^{'}s.t.k{'}\neq k}\{a(i,k^{'})+s(i,k^{'})\} \tag{1} r(i,k)←s(i,k)−k′s.t.k′=kmax{a(i,k′)+s(i,k′)}(1)
In the first iteration, because the availabilities are zero, r ( i , k ) r(i,k) r(i,k) is set to the input similarity between point i i i and point k k k as its exemplar, minus the largest of the similarities between point i i i and other candidate exemplars. This competitive update is data-driven and does not take into account how many other points favor each candidate exemplar. In later iterations, when some points are effectively assigned to other exemplars, their availabilities will drop below zero as prescribed by the update rule below. These negative availabilities will decrease the effective values of some of the input similarities s ( i , k ′ ) s(i,k′) s(i,k′) in the above rule, removing the corresponding candidate exemplars from competition. For k = i k = i k=i , the responsibility r ( k , k ) r(k,k) r(k,k) is set to the input preference that point k k k be chosen as an exemplar, s ( k , k ) s(k,k) s(k,k) , minus the largest of the similarities between point i i i and all other candidate exemplars. This “self-responsibility” reflects accumulated evidence that point k k k is an exemplar, based on its input preference tempered by how ill-suited it is to be assigned to another exemplar.
数据点之间有两种消息交换,每种都考虑到不同类型的竞争。可以在任何阶段组合消息,以确定哪些点是示例,对于其他每个点,它属于哪些示例。从数据点 i i i 发送到候选样本点 k k k 的 “职责responsibility” r ( i , k ) r(i,k) r(i,k) 反映了考虑到点 i i i 的其他潜在样本,点 k k k 作为点 i i i 的样本有多合适的累积证据(图1B)。从候选样本点 k k k 发送到点 i i i 的 “可用性availability” a ( i , k ) a(i,k) a(i,k)反映了点 i i i 选择点 k k k 作为其样本是多么合适的累积证据,同时考虑到来自点 k k k 应该是样本的其他点的支持(图1C)。 r ( i , k ) r(i,k) r(i,k) 和 a ( i , k ) a(i,k) a(i,k) 可视为对数概率比。首先,可用性被初始化为零: a ( i , k ) = 0 a(i,k) = 0 a(i,k)=0 。然后,使用规则计算其responsibility
r ( i , k ) ← s ( i , k ) − max k ′ s . t . k ′ ≠ k { a ( i , k ′ ) + s ( i , k ′ ) } (1) r(i,k)\leftarrow s(i,k) - \max_{k^{'}s.t.k{'}\neq k}\{a(i,k^{'})+s(i,k^{'})\} \tag{1} r(i,k)←s(i,k)−k′s.t.k′=kmax{a(i,k′)+s(i,k′)}(1)
在第一次迭代中,因为 availability 为零,所以 r ( i , k ) r(i,k) r(i,k) 被设置为点 i i i 和点 k k k 之间的输入相似度作为其样本,减去点 i i i 和其他候选样本之间的最大相似度。这种竞争性的更新是数据驱动的,没有考虑每个候选样本有多少其他优势。在以后的迭代中,当一些点被有效地分配给其他样本时,它们的 availability 将下降到零以下,如下面的更新规则所规定的。这些负的 availability 将降低上述规则中一些输入相似性 s ( i , k ′ ) s(i,k′) s(i,k′) 的有效值,从竞争中移除相应的候选样本。对于 k = i k = i k=i ,responsibility r ( k , k ) r(k,k) r(k,k) 被设置为输入偏好,即点 k k k 被选择为样本 s ( k , k ) s(k,k) s(k,k) ,减去点 i i i 和所有其他候选样本之间的最大相似度。这种 “self-responsibility” 反映了积累的证据,即点 k k k 是一个样本,基于它的输入偏好,再加上它被分配给另一个样本的不合适程度。
Whereas the above responsibility update lets all candidate exemplars compete for ownership of a data point, the following availability update gathers evidence from data points as to whether each candidate exemplar would make a good exemplar:
a ( i , k ) ← min { 0 , r ( k , k ) + ∑ i ′ s . t . i ′ ∉ i , k max 0 , r ( i ′ , k ) } (2) a(i,k)\leftarrow \min\{0,r(k,k)+\sum_{i^{'}s.t.i^{'}\notin i,k}\max{0,r(i^{'},k)}\} \tag{2} a(i,k)←min{0,r(k,k)+i′s.t.i′∈/i,k∑max0,r(i′,k)}(2)
The availability a ( i , k ) a(i,k) a(i,k) is set to the self-responsibility r(k,k) plus the sum of the positive responsibilities candidate exemplar k receives from other points. Only the positive portions of incoming responsibilities are added, because it is only necessary for a good exemplar to explain some data points well (positive responsibilities), regardless of how poorly it explains other data points (negative responsibilities). If the self-responsibility r ( k , k ) r(k,k) r(k,k) is negative (indicating that point k k k is currently better suited as belonging to another exemplar rather than being an exemplar itself), the availability of point k as an exemplar can be increased if some other points have positive responsibilities for point k being their exemplar. To limit the influence of strong incoming positive responsibilities, the total sum is thresholded so that it cannot go above zero. The “self-availability” a ( k , k ) a(k,k) a(k,k) is updated differently:
a ( k , k ) ← ∑ i ′ s . t . i ′ ≠ k max { 0 , r ( i ′ , k ) } (3) a(k,k)\leftarrow\sum_{i^{'}s.t.i^{'}\neq k}\max\{0,r(i^{'},k)\} \tag{3} a(k,k)←i′s.t.i′=k∑max{0,r(i′,k)}(3)
This message reflects accumulated evidence that point k is an exemplar, based on the positive responsibilities sent to candidate exemplar k from other points.
鉴于上述 responsibility 更新使所有候选样例都能争夺数据点的所有权,而以下 availability 更新会从数据点收集证据,以证明每个候选样例是否都可以成为一个好的样例:
a ( i , k ) ← min { 0 , r ( k , k ) + ∑ i ′ s . t . i ′ ∉ i , k max 0 , r ( i ′ , k ) } (2) a(i,k)\leftarrow \min\{0,r(k,k)+\sum_{i^{'}s.t.i^{'}\notin i,k}\max{0,r(i^{'},k)}\} \tag{2} a(i,k)←min{0,r(k,k)+i′s.t.i′∈/i,k∑max0,r(i′,k)}(2)
availability a ( i , k ) a(i,k) a(i,k) 被设置为 self-responsibility r ( k , k ) r(k,k) r(k,k) 加上候选范例 k k k 从其他点接收到的正responsibility 之和。只添加了引入responsibility 的正数部分,因为一个好的范例只需要很好地解释一些数据点(positive responsibilities),而不管它解释其他数据点(negative responsibilities)有多差。如果self-responsibility r ( k , k ) r(k,k) r(k,k) 为负(表明 k k k 点目前更适合作为另一个样本而不是样本本身),那么如果其他一些点对 k k k 点作为其样本具有正的responsibility ,则 k k k 点作为样本的 availability 可以增加。为了限制强大的positive responsibilities的影响,对总和设置阈值,以使总和不能超过零。 “self-responsibility” a ( k , k ) a(k,k) a(k,k)的更新方式有所不同:
a ( k , k ) ← ∑ i ′ s . t . i ′ ≠ k max { 0 , r ( i ′ , k ) } (3) a(k,k)\leftarrow\sum_{i^{'}s.t.i^{'}\neq k}\max\{0,r(i^{'},k)\} \tag{3} a(k,k)←i′s.t.i′=k∑max{0,r(i′,k)}(3)
该消息基于从其他点发送到候选样例 k k k 的positive responsibilities,反映了点 k k k 是样例的累积证据。
The above update rules require only simple, local computations that are easily implemented (2), and messages need only be exchanged between pairs of points with known similarities. At any point during affinity propagation, availabilities and responsibilities can be combined to identify exemplars. For point i i i , the value of k k k that maximizes a ( i , k ) + r ( i , k ) a(i,k) + r(i,k) a(i,k)+r(i,k) either identifies point i i i as an exemplar if k = i k = i k=i , or identifies the data point that is the exemplar for point i i i. The message-passing procedure may be terminated after a fixed number of iterations, after changes in the messages fall below a threshold, or after the local decisions stay constant for some number of iterations. When updating the messages, it is important that they be damped to avoid numerical oscillations that arise in some circumstances. Each message is set to λ \lambda λ times its value from the previous iteration plus 1 – λ 1 – \lambda 1–λ times its prescribed updated value, where the damping factor λ \lambda λ is between 0 and 1. In all of our experiments (3), we used a default damping factor of λ = 0.5 \lambda = 0.5 λ=0.5 , and each iteration of affinity propagation consisted of (i) updating all responsibilities given the availabilities, (ii) updating all availabilities given the responsibilities, and (iii) combining availabilities and responsibilities to monitor the exemplar decisions and terminate the algorithm when these decisions did not change for 10 iterations.
上面的更新规则仅需要简单的本地计算即可轻松实现,并且仅需要在具有相似相似性的成对点之间交换消息。在AP聚类算法过程中的任何时候,都可以将 availabilities 和 responsibilities 进行组合以识别示例。对于点 i i i ,如果 k = i k = i k=i ,则最大化 a ( i , k ) + r ( i , k ) a(i,k)+ r(i,k) a(i,k)+r(i,k) 的 k k k 值会将点 i i i 识别为示例,或者将数据点识别为点 i i i 的示例。消息传递过程可以在固定数量的迭代之后,消息中的变化降至阈值以下之后,或者在本地决策在某些迭代中保持恒定之后终止。更新消息时,请务必对它们进行阻尼处理,以避免在某些情况下出现数值振荡。每个消息的值设置为上次迭代的值的 λ \lambda λ 倍加上其规定的更新值的 1 − λ 1-\lambda 1−λ倍,其中阻尼因子 λ \lambda λ 在0到1之间。在我们所有的实验中,我们使用默认阻尼因子 λ = 0.5 \lambda = 0.5 λ=0.5,并且AP聚类算法的每个迭代包括(i)给定availabilities 更新所有responsibilities ,(ii)给定responsibilities 更新所有availabilities ,以及(iii)结合availabilities 和responsibilities 来监视示例决策,并在10次迭代中这些决策不变时终止算法。
Figure 1A shows the dynamics of affinity propagation applied to 25 two-dimensional data points (3), using negative squared error as the similarity. One advantage of affinity propagation is that the number of exemplars need not be specified beforehand. Instead, the appropriate number of exemplars emerges from the messagepassing method and depends on the input exemplar preferences. This enables automatic model selection, based on a prior specification of how preferable each point is as an exemplar. Figure 1D shows the effect of the value of the common input preference on the number of clusters. This relation is nearly identical to the relation found by exactly minimizing the squared error (2).
图1A显示了使用负平方误差作为相似度,将动态相似性传播应用于25个二维数据点的动力学。AP聚类算法的一个优点是无需预先指定示例数。取而代之的是,适当的示例数量从message-passing算法中出现,并取决于输入的示例首选项。这样就可以根据每个点作为示例的优选程度的现有规范自动选择模型。图1D显示了公共输入首选项的值对簇数的影响。该关系与通过最小化平方误差所找到的关系几乎相同。
We next studied the problem of clustering images of faces using the standard optimization criterion of squared error. We used both affinity propagation and k-centers clustering to identify exemplars among 900 grayscale images extracted from the Olivetti face database (3). Affinity propagation found exemplars with much lower squared error than the best of 100 runs of k-centers clustering (Fig. 2A), which took about the same amount of computer time. We asked whether a huge number of random restarts of k-centers clustering could achieve the same squared error. Figure 2B shows the error achieved by one run of affinity propagation and the distribution of errors achieved by 10,000 runs of k-centers clustering, plotted against the number of clusters. Affinity propagation uniformly achieved much lower error in more than two orders of magnitude less time. Another popular optimization criterion is the sum of absolute pixel differences (which better tolerates outlying pixel intensities), so we repeated the above procedure using this error measure. Affinity propagation again uniformly achieved lower error (Fig. 2C).
接下来,我们使用平方误差的标准优化准则研究人脸图像聚类的问题。我们使用AP聚类算法和k-中心聚类算法来识别从Olivetti人脸数据库提取的900幅灰度图像中的样本。AP聚类算法所发现的示例的平方误差要比100个k-中心聚类算法的最佳结果(图2A)要低得多,后者花费了相同的计算机时间。我们询问是否大量重启k-中心聚类算法可以实现相同的平方误差。图2B显示了通过运行一次AP聚类算法获得的误差以及通过运行10,000个k-中心聚类算法获得的误差分布,并针对聚类数进行了绘制。AP聚类算法在少两个多数量级的时间内均匀地实现了低得多的误差。另一个流行的优化标准是绝对像素差的总和(可以更好地容忍离群的像素强度),因此我们使用此误差度量重复了上述过程。AP聚类算法再次均匀地实现了较低的误差(图2C)。
Fig. 2. Clustering faces. Exemplars minimizing the standard squared error measure of similarity were identified from 900 normalized face images (3). For a common preference of −600, affinity propagation found 62 clusters, and the average squared error was 108. For comparison, the best of 100 runs of k-centers clustering with different random initializations achieved a worse average squared error of 119. (A) The 15 images with highest squared error under either affinity propagation or k-centers clustering are shown in the top row. The middle and bottom rows show the exemplars assigned by the two methods, and the boxes show which of the two methods performed better for that image, in terms of squared error. Affinity propagation found higher-quality exemplars. (B) The average squared error achieved by a single run of affinity propagation and 10,000 runs of k-centers clustering, versus the number of clusters. The colored bands show different percentiles of squared error, and the number of exemplars corresponding to the result from (A) is indicated. © The above procedure was repeated using the sum of absolute errors as the measure of similarity, which is also a popular optimization criterion.
**图2.**聚类面。从900个标准化的面部图像中识别出最小化相似度的标准平方误差度量的示例。对于-600的一般偏好,AP聚类算法找到了62个簇,平均平方误差为108。为进行比较,使用不同随机初始化的100个k-中心聚类的最佳运行获得了较差的平均平方误差119。 **(A)**第一行显示在AP聚类算法或k-中心聚类下具有最高平方误差的15张图像。中间和底部各行显示了这两种方法分配的样本,而方框显示了根据平方误差,这两种方法中哪一种对图像效果更好。AP聚类算法发现了更高质量的样本。 **(B)**相对于聚类数,单次AP聚类算法和10,000个k-中心聚类获得的平均平方误差。彩色带显示平方误差的不同百分位数,并表示与(A)结果相对应的示例数。 **(C)**使用绝对误差之和作为相似性的度量重复上述过程,这也是一种流行的优化标准。
Many tasks require the identification of exemplars among sparsely related data, i.e., where most similarities are either unknown or large and negative. To examine affinity propagation in this context, we addressed the task of clustering putative exons to find genes, using the sparse similarity matrix derived from microarray data and reported in (4). In that work, 75,066 segments of DNA (60 bases long) corresponding to putative exons were mined from the genome of mouse chromosome 1. Their transcription levels were measured across 12 tissue samples, and the similarity between every pair of putative exons (data points) was computed. The measure of similarity between putative exons was based on their proximity in the genome and the degree of coordination of their transcription levels across the 12 tissues. To account for putative exons that are not exons (e.g., introns), we included an additional artificial exemplar and determined the similarity of each other data point to this “nonexon exemplar” using statistics taken over the entire data set. The resulting 75,067 × 75,067 similarity matrix (3) consisted of 99.73% similarities with values of − ∞ −∞ −∞, corresponding to distant DNA segments that could not possibly be part of the same gene. We applied affinity propagation to this similarity matrix, but because messages need not be exchanged between point i i i and k k k if s ( i , k ) = − ∞ s(i,k) = −∞ s(i,k)=−∞, each iteration of affinity propagation required exchanging messages between only a tiny subset (0.27% or 15 million) of data point pairs.
许多任务需要在稀疏相关的数据中识别样本,也就是说,在这些数据中,大多数相似性要么是未知的,要么是大而负面的。为了研究这种背景下的AP聚类算法,我们利用从微阵列数据中获得的稀疏相似性矩阵(见第(4)节)提出了聚类假设外显子以寻找基因的任务。在这项研究中,我们从小鼠1号染色体的基因组中提取了75066段DNA片段(60碱基长),这些片段与假定的外显子相对应。在12个组织样本中测量了它们的转录水平,并计算了每对假定外显子(数据点)之间的相似性。假设外显子之间的相似性是基于它们在基因组中的接近程度以及它们在12种组织中转录水平的协调程度。为了说明不是外显子的推定外显子(例如内含子),我们加入了一个额外的人工样本,并使用整个数据集的统计数据确定了每个数据点与此“非外显子样本”的相似性。由此得到的 75067×75067 相似矩阵与 − ∞ -∞ −∞ 值的相似度为 99.73%,对应于不可能是同一基因一部分的远缘DNA片段。我们将相似性传播应用到这个相似性矩阵中,但是由于如果 s ( i , k ) = − ∞ s(i,k)=-∞ s(i,k)=−∞ 时,不需要在点 i i i 和 k k k 之间交换消息,所以AP聚类算法的每次迭代只需要在数据点对的一小部分(0.27%或1500万)之间交换消息。
Figure 3A illustrates the identification of gene clusters and the assignment of some data points to the nonexon exemplar. The reconstruction errors for affinity propagation and k-centers clustering are compared in Fig. 3B. For each number of clusters, affinity propagation was run once and took 6 min, whereas k-centers clustering was run 10,000 times and took 208 hours. To address the question of how well these methods perform in detecting bona fide gene segments, Fig. 3C plots the true-positive (TP) rate against the false-positive (FP) rate, using the labels provided in the RefSeq database (5). Affinity propagation achieved significantly higher TP rates, especially at low FP rates, which are most important to biologists. At a FP rate of 3%, affinity propagation achieved a TP rate of 39%, whereas the best k-centers clustering result was 17%. For comparison, at the same FP rate, the best TP rate for hierarchical agglomerative clustering (2) was 19%, and the engineering tool described in (4), which accounts for additional biological knowledge, achieved a TP rate of 43%.
图3A说明了基因簇的识别和一些数据点的分配。图3B比较了AP聚类算法和k-中心聚类的重建误差。对于每个数量的聚类,AP聚类算法运行一次,耗时6分钟,而k-中心聚类算法运行10000次,耗时208小时。为了解决这些方法在检测真实基因片段方面的表现如何的问题,图 3C 使用RefSeq数据库中提供的标签绘制了真正例(TP)率和假正例(FP)率。AP聚类算法实现了更高的真正例率,尤其是在低假正例率下,这对生物学家而言最重要。在假正例率为3%时,AP聚类算法的真正例率为39%,而最佳k-中心聚类结果为17%。作为比较,在相同的假正例率下,层次聚集聚类的最佳真正例率为19%,而(4)中描述的工程工具(它解释了额外的生物学知识)实现了43%的真正例率。
Fig. 3. Detecting genes. Affinity propagation was used to detect putative exons (data points) comprising genes from mouse chromosome 1. Here, squared error is not appropriate as a measure of similarity, but instead similarity values were derived from a cost function measuring proximity of the putative exonsin the genome and co expression of the putative exons across 12 tissue samples (3). (A) A small portion of the data and the emergence of clusters during each iteration of affinity propagation are shown. In each picture, the 100 boxes outlined in black correspond to 100 data points (from a total of 75,066 putative exons), and the 12 colored blocks in each box indicate the transcription levels of the corresponding DNA segment in 12 tissue samples. The box on the far left corresponds to an artificial data point with infinite preference that is used to account for nonexon regions (e.g., introns). Lines connecting data points indicate potential assignments, where gray lines indicate assignments that currently have weak evidence and solid lines indicate assignments that currently have strong evidence. (B) Performance on minimizing the reconstruction error of genes, for different numbers of detected clusters. For each number of clusters, affinity propagation took 6 min, whereas 10,000 runs of k-centers clustering took 208 hours on the same computer. In each case, affinity propagation achieved a significantly lower reconstruction error than k-centers clustering. © A plot of true-positive rate versus false-positive rate for detecting exons [using labels from RefSeq (5)] shows that affinity propagation also performs better at detecting biologically verified exons than k-centers clustering.
图3. 检测基因。AP聚类算法用于检测包含来自小鼠染色体1的基因的推定外显子(数据点)。此处,平方误差不适合作为相似性的量度,而是相似性值是通过测量该基因组中推定外显子的接近度的成本函数得出的和推定外显子在12个组织样品中的共表达。(A) 显示了数据的一小部分和AP聚类算法的每次迭代过程中簇的出现。在每张图片中,黑色轮廓的100个框对应于100个数据点(来自总共75,066个假定的外显子),并且每个框中的12个彩色块表示12个组织样本中相应DNA片段的转录水平。最左侧的框对应于具有无限优先级的人工数据点,该人工数据点用于说明非外显子区域(例如内含子)。连接数据点的线表示潜在的分配,其中灰线表示当前证据不足的分配,实线表示当前证据较强的分配。(B) 对于不同数目的检测到的簇,在最小化基因的重建误差上的性能。对于每个数量的群集,AP聚类算法花费6分钟,而在同一台计算机上进行10,000次k-中心群集花费了208小时。在每种情况下,AP聚类算法实现的重建误差均远低于k-中心聚类。 (C) 检测外显子的真阳性率与假阳性率的关系图(使用来自RefSeq的标记)显示,AP聚类算法在检测生物学验证的外显子方面也比k-中心聚类表现更好。
Affinity propagation’s ability to operate on the basis of nonstandard optimization criteria makes it suitable for exploratory data analysis using unusual measures of similarity. Unlike metric-space clustering techniques such as k-means clustering (1), affinity propagation can be applied to problems where the data do not lie in a continuous space. Indeed, it can be applied to problems where the similarities are not symmetric [i.e., s ( i , k ) ≠ s ( k , i ) s(i,k) ≠ s(k,i) s(i,k)=s(k,i)] and to problems where the similarities do not satisfy the triangle inequality [i.e., s ( i , k ) < s ( i , j ) + s ( j , k ) s(i,k) < s(i,j) + s( j,k) s(i,k)<s(i,j)+s(j,k)]. To identify a small number of sentences in a draft of this manuscript that summarize other sentences, we treated each sentence as a “bag of words” (6) and computed the similarity of sentence i i i to sentence k k k based on the cost of encoding the words in sentence i i i using the words in sentence k k k . We found that 97% of the resulting similarities ( 2 , 3 ) (2, 3) (2,3) were not symmetric. The preferences were adjusted to identify (using λ = 0.8 \lambda = 0.8 λ=0.8) different numbers of representative exemplar sentences (2), and the solution with four sentences is shown in Fig. 4A.
AP聚类算法基于非标准优化准则的能力使得它适合于使用不寻常的相似性度量进行探索性数据分析。与k-均值聚类等度量空间聚类技术不同,AP聚类算法可以应用于数据不在连续空间中的问题。实际上,它可以应用于相似性不对称的问题[即 s ( i , k ) ≠ s ( k , i ) s(i,k)≠s(k,i) s(i,k)=s(k,i)]和相似性不满足三角形不等式[即 s ( i , k ) s(i,k) s(i,k)]。为了找出手稿草稿中总结其他句子的少量句子,我们将每个句子作为一个“单词包”,并根据对 k k k 句子中单词的编码成本计算句子与 k k k 句子的相似度。我们发现97%的相似性 ( 2 , 3 ) (2,3) (2,3) 不是对称的。调整偏好以识别(使用 λ = 0.8 \lambda=0.8 λ=0.8)不同数量的代表性例句,四个句子的解决方案如图4A所示。
Fig. 4. Identifying key sentences and air-travel routing. Affinity propagation can be used to explore the identification of exemplars on the basis of nonstandard optimization criteria. (A) Similarities between pairs of sentences in a draft of this manuscript were constructed by matching words. Four exemplar sentences were identified by affinity propagation and are shown. (B) Affinity propagation was applied to similarities derived from air-travel efficiency (measured by estimated travel time) between the 456 busiest commercial airports in Canada and the United States—the travel times for both direct flights (shown in blue) and indirect flights (not shown), including the mean transfer time of up to a maximum of one stopover, were used as negative similarities (3). © Seven exemplars identified by affinity propagation are color-coded, and the assignments of other cities to these exemplars is shown. Cities located quite near to exemplar cities may be members of other more distant exemplars due to the lack of direct flights between them (e.g., Atlantic City is 100 km from Philadelphia, but is closer in flight time to Atlanta). (D) The inset shows that the Canada-USA border roughly divides the Toronto and Philadelphia clusters, due to a larger availability of domestic flights compared to international flights. However, this is not the case on the west coast as shown in (E), because extraordinarily frequent airline service between Vancouver and Seattle connects Canadian cities in the northwest to Seattle.
**图4.**识别关键句子和空中旅行路线。AP聚类算法可用于基于非标准优化标准探索示例的识别。 **(A)**该手稿草稿中的成对句子之间的相似性是通过匹配单词来构造的。通过AP聚类算法识别并显示了四个示例性句子。 **(B)*将AP聚类算法应用于加拿大和美国456个最繁忙的商业机场之间的空中旅行效率(通过估计的旅行时间衡量)得出的相似性-直飞(蓝色显示)和间接飞行的旅行时间(未显示)(包括最多最多一个中途停留的平均转移时间)被用作负相似度(3)*。 **(C)**通过AP聚类算法识别的七个样本进行了颜色编码,并显示了其他城市对这些样本的分配。由于城市之间缺乏直飞航班,因此距离范例城市很近的城市可能是其他较遥远的范例的成员(例如,大西洋城距离费城100公里,但到亚特兰大的飞行时间更近)。 **(D)**结果表明,由于与国际航班相比,国内航班的可用性更大,因此加拿大与美国的边界将多伦多和费城的集群大致分为两部分。但是,(E)所示的西海岸情况并非如此,因为温哥华和西雅图之间非常频繁的航空服务将西北部的加拿大城市连接到西雅图。
We also applied affinity propagation to explore the problem of identifying a restricted number of Canadian and American cities that are most easily accessible by large subsets of other cities, in terms of estimated commercial airline travel time. Each data point was a city, and the similarity s ( i , k ) s(i,k) s(i,k) was set to the negative time it takes to travel from city i i i to city k k k by airline, including estimated stopover delays (3). Due to headwinds, the transit time was in many cases different depending on the direction of travel, so that 36% of the similarities were asymmetric. Further, for 97% of city pairs i i i and k k k, there was a third city j j j such that the triangle inequality was violated, because the trip from i i i to k k k included a long stopover delay in city j j j so it took longer than the sum of the durations of the trips from i i i to j j j and j j j to k k k. When the number of “most accessible cities” was constrained to be seven (by adjusting the input preference appropriately), the cities shown in Fig. 4, B to E, were identified. It is interesting that several major cities were not selected, either because heavy international travel makes them inappropriate as easily accessible domestic destinations (e.g., New York City, Los Angeles) or because their neighborhoods can be more efficiently accessed through other destinations (e.g., Atlanta, Philadelphia, and Minneapolis account for Chicago’s destinations, while avoiding potential airport delays).
我们还应用了相似性传播来探索这样的问题,即根据估计的商业航空旅行时间,识别最容易被其他城市的大子集访问的有限数量的加拿大和美国城市。每个数据点是一个城市,相似性 s ( i , k ) s(i,k) s(i,k) 被设置为乘飞机从城市 i i i 到城市 k k k 的负时间,包括估计的中途停留时间。由于逆风,运输时间在许多情况下因行驶方向而异,因此36%的相似性是不对称的。此外,对于97%的城市对 i i i 和 k k k ,存在第三个城市 j j j ,从而违反了三角形不等式,因为从 i i i 到 k k k 的行程包括在城市 j j j 中的长的中途停留延迟,所以它花费的时间比从 i i i 到j和从 j j j 到 k k k 的行程持续时间的总和更长。当“最容易到达的城市”的数量被限制为7时(通过适当地调整输入偏好),图4中所示的城市B到E被识别。有趣的是,有几个主要城市没有被选中,要么是因为大量的国际旅行使它们不适合作为容易到达的国内目的地(如纽约市、洛杉矶),要么是因为它们的邻近地区可以通过其他目的地更有效地到达(如亚特兰大、费城和明尼阿波利斯占了芝加哥的目的地,同时避免了潜在的机场延误)。
Affinity propagation can be viewed as a method that searches for minima of an energy function (7) that depends on a set of N N N hidden labels, c 1 , … , c N c_1,…,c_N c1,…,cN, corresponding to the N N N data points. Each label indicates the exemplar to which the point belongs, so that s ( i , c i ) s(i,c_i) s(i,ci) is the similarity of data point i i i to its exemplar. c i = i c_i= i ci=i is a special case indicating that point i i i is itself an exemplar, so that s ( i , c i ) s(i,c_i) s(i,ci) is the input preference for point i i i . Not all configurations of the labels are valid; a configuration c is valid when for every point i i i , if some other point i ′ i′ i′ has chosen i i i as its exemplar (i.e., c i ′ = i c_{i′}= i ci′=i), then i i i must be an exemplar (i.e., c i = i c_i= i ci=i). The energy of a valid configuration is E ( c ) = − ∑ i = 1 N s ( i , c i ) E(c) = −∑_{i=1}^N s(i,c_i) E(c)=−∑i=1Ns(i,ci). Exactly minimizing the energy is computationally intractable, because a special case of this minimization problem is the NP-hard k-median problem (8). However, the update rules for affinity propagation correspond to fixed-point recursions for minimizing a Bethe free-energy (9) approximation. Affinity propagation is most easily derived as an instance of the max-sum algorithm in a factor graph (10) describing the constraints on the labels and the energy function (2).
AP聚类算法可以看作是一种搜索能量函数的极小值的方法,该能量函数依赖于与 N N N 个数据点相对应的一组 N N N 个隐藏标签 c 1 , … , c N c_1,…,c_N c1,…,cN 。每个标签都指示该点所属的样本,因此 s ( i , c i ) s(i,c_i) s(i,ci) 是数据点 i i i 与其样本的相似性。 c i = i c_i = i ci=i 是一种特殊情况,指示点 i i i 本身就是一个示例,因此 s ( i , c i ) s(i,c_i) s(i,ci) 是点 i i i 的输入偏好。并非标签的所有配置均有效。当对于每个点 i i i ,如果其他某个点 i ′ i' i′ 选择了i作为其示例(即 c i ′ = i c_{i'}= i ci′=i),则配置 c 就是有效的,那么 i i i 必须是一个示例(即 c i = i c_i = i ci=i )。有效配置的能量为 E ( c ) = − ∑ i = 1 N s ( i , c i ) E(c)= -∑_{i = 1}^ N s(i,c_i) E(c)=−∑i=1Ns(i,ci) 。精确地最小化能量在计算上是棘手的,因为这种最小化问题的特殊情况是NP-hard k中值问题。但是,用于AP聚类算法的更新规则与定点递归相对应,以最小化Bethe自由能近似值。AP聚类算法最容易在因子图中作为max-sum算法的实例得出,该图描述了标签和能量函数的约束。
In some degenerate cases, the energy function may have multiple minima with corresponding multiple fixed points of the update rules, and these may prevent convergence. For example, if s ( 1 , 2 ) = s ( 2 , 1 ) s(1,2) = s(2,1) s(1,2)=s(2,1) and s ( 1 , 1 ) = s ( 2 , 2 ) s(1,1) = s(2,2) s(1,1)=s(2,2) , then the solutions c 1 = c 2 = 1 c_1= c_2= 1 c1=c2=1 and c 1 = c 2 = 2 c_1= c_2= 2 c1=c2=2 both achieve the same energy. In this case, affinity propagation may oscillate, with both data points alternating between being exemplars and nonexemplars. In practice, we found that oscillations could always be avoided by adding a tiny amount of noise to the similarities to prevent degenerate situations, or by increasing the damping factor.
在某些退化情形下,能量函数可能具有多个极小值,且更新规则的多个不动点可能会阻止收敛。例如,如果 s ( 1 , 2 ) = s ( 2 , 1 ) s(1,2) = s(2,1) s(1,2)=s(2,1) 和 s ( 1 , 1 ) = s ( 2 , 2 ) s(1,1) = s(2,2) s(1,1)=s(2,2) ,则解 c 1 = c 2 = 1 c_1= c_2= 1 c1=c2=1 和 c 1 = c 2 = 2 c_1= c_2= 2 c1=c2=2 都获得相同的能量。在这种情况下,亲和性传播可能会振荡,两个数据点在样本和非样本之间交替。在实践中,我们发现通过在相似点上添加少量的噪声来防止退化情况,或者通过增加阻尼因子来避免振荡。
Affinity propagation has several advantages over related techniques. Methods such as k-centers clustering (1), k-means clustering (1), and the expectation maximization (EM) algorithm (11) store a relatively small set of estimated cluster centers at each step. These techniques are improved upon by methods that begin with a large number of clusters and then prune them (12), but they still rely on random sampling and make hard pruning decisions that cannot be recovered from. In contrast, by simultaneously considering all data points as candidate centers and gradually identifying clusters, affinity propagation is able to avoid many of the poor solutions caused by unlucky initializations and hard decisions. Markov chain Monte Carlo techniques (13) randomly search for good solutions, but do not share affinity propagation’s advantage of considering many possible solutions all at once.
与相关技术相比,AP聚类算法有几个优点。像k-中心聚类、k-均值聚类和期望最大化(EM)算法这样的方法在每个步骤存储一个相对较小的估计聚类中心集。这些技术通过从大量的簇开始,然后对它们进行修剪的方法得到了改进,但是它们仍然依赖于随机抽样,并且做出无法恢复的硬修剪决策。相反,通过同时考虑所有数据点作为候选中心并逐步识别簇,AP聚类算法能够避免由于不吉利的初始化和艰难的决策而导致的许多糟糕的解决方案。马尔可夫链蒙特卡罗技术随机搜索好的解决方案,但不共享AP聚类算法的优点,即一次考虑许多可能的解决方案。
Hierarchical agglomerative clustering (14) and spectral clustering (15) solve the quite different problem of recursively comparing pairs of points to find partitions of the data. These techniques do not require that all points within a cluster be similar to a single center and are thus not well-suited to many tasks. In particular, two points that should not be in the same cluster may be grouped together by an unfortunate sequence of pairwise groupings.
层次聚集聚类和谱聚类解决了递归比较点对对以找到数据分区的完全不同的问题。这些技术不需要群集中的所有点都类似于单个中心,因此不适合许多任务。特别地,可以通过不幸的成对分组序列将不应该在同一聚类中的两个点分组在一起。
In (8), it was shown that the related metric k-median problem could be relaxed to form a linear program with a constant factor approximation. There, the input was assumed to be metric, i.e., nonnegative, symmetric, and satisfying the triangle inequality. In contrast, affinity propagation can take as input general nonmetric similarities. Affinity propagation also provides a conceptually new approach that works well in practice. Whereas the linear programming relaxation is hard to solve and sophisticated software packages need to be applied (e.g., CPLEX), affinity propagation makes use of intuitive message updates that can be implemented in a few lines of code (2).
在(8)中,表明相关的度量k-中值问题可以放宽以形成具有恒定因子近似的线性程序。在那里,假定输入为度量,即非负,对称并满足三角不等式。相反,AP聚类算法可以将一般的非度量相似性作为输入。AP聚类算法还提供了一种概念上可行的新方法。线性规划的松弛难以解决,需要应用复杂的软件包(例如CPLEX),而亲缘传播则利用直观的消息更新功能,可以在几行代码中实现。
Affinity propagation is related in spirit to techniques recently used to obtain record-breaking results in quite different disciplines (16). The approach of recursively propagating messages (17) in a “loopy graph” has been used to approach Shannon’s limit in error-correcting decoding (18, 19), solve random satisfiability problems with an order-of-magnitude increase in size (20), solve instances of the NP-hard twodimensional phase-unwrapping problem (21), and efficiently estimate depth from pairs of stereo images (22). Yet, to our knowledge, affinity propagation is the first method to make use of this idea to solve the age-old, fundamental problem of clustering data. Because of its simplicity, general applicability, and performance, we believe affinity propagation will prove to be of broad value in science and engineering.
从本质上讲,AP聚类算法与最近用于在完全不同的学科中获得破记录的结果的技术有关。在“循环图”中递归传播消息的方法已被用于在纠错解码中接近香农极限,解决了大小可乘数级的随机可满足性问题,解决NP-hard二维相位解缠问题的实例,并根据成对的立体图像有效地估计深度。然而,据我们所知,AP聚类算法是利用此思想解决群集数据的古老基础问题的第一种方法。由于它的简单性,普遍适用性和性能,我们相信AP聚类算法将被证明在科学和工程领域具有广泛的价值。
参考文献
References