✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统
信号处理 图像处理 路径规划 元胞自动机 无人机
❤️ 内容介绍
在流体力学领域,层流是指在平行板之间的流动,其中流体沿着平行的路径流动,而不发生明显的横向混合。层流现象在许多工程和科学应用中都非常重要,因此研究和理解层流的速度、压力和温度分布是至关重要的。
为了解决平行板之间层流的速度、压力和温度分布,工程师和科学家使用了一种称为有限体积法 (FVM) 的数值方法。有限体积法是一种将连续介质方程离散化的方法,它将流体域划分为许多小的体积单元,并在每个体积单元中计算流体的平均速度、压力和温度。
在有限体积法中,流体域被划分为一个个小的体积单元,每个体积单元都有一个中心点和相邻的体积单元。通过应用质量守恒、动量守恒和能量守恒等基本方程,可以在每个体积单元中建立离散方程。这些离散方程可以通过迭代求解来获得整个流体域的速度、压力和温度分布。
在层流问题中,SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) 算法是一种常用的求解方法。SIMPLE算法通过耦合速度和压力来解决流体方程,并使用松弛因子来加速求解过程。该算法通过迭代计算速度和压力的修正值,直到满足收敛准则为止。
在使用有限体积法和SIMPLE算法求解平行板之间层流的速度、压力和温度时,需要进行一些前期准备工作。首先,需要定义流体域的几何形状和边界条件。然后,需要选择适当的网格划分方法,并计算每个体积单元的几何参数和初始值。接下来,通过迭代求解离散方程,可以得到流体域的速度、压力和温度分布。
在求解过程中,需要注意选择合适的数值格式和求解器,以确保结果的准确性和稳定性。此外,还需要进行网格收敛性和物理模型验证,以验证数值解的可靠性。
总之,基于有限体积法和SIMPLE算法求解平行板之间层流的速度、压力和温度是一项复杂而重要的工作。通过合理的几何划分、边界条件的定义和数值求解的迭代过程,可以得到准确和可靠的结果。这些结果对于理解和优化层流现象在工程和科学应用中的影响具有重要意义。
🔥核心代码
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Finite Volume Method with SIMPLE algorithm% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear,clc,close allglobal Fw Fe Fs Fn DF aW aE aS aN aP bP dU dV%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% CHANNEL FLOW PROBLEM WITH CONSTANT TEMPERATURE OR HEAT FLUX WALLS% GeometryH = 0.01; % Height of channel in y-direction(m)L = 10*H; % Length of cavity in x-direction (m)% Grid geometryNx = 200; % Number of main grid points in x-direction within domaindx = L/Nx; % Grid spacing in x-directionNy = 40; % Number of main grid points in y-direction within domaindy = H/Ny; % Grid spacing in y-directiondz = 0.01; % Width in z-direction for flux calculations (m)x = dx/2:dx:L-dx/2; % x-locations of main grid points (m)xu = 0:dx:L; % x-locations of u-velocities (m)y = dy/2:dy:H-dy/2; % y-locations of main grid points (m)yv = 0:dy:H; % y-locations of v-velocities (m)iu = 1:Nx+1; Ju = 2:Ny+1; % Interior node numbers for uIv = 2:Nx+1; jv = 1:Ny+1; % Interior node numbers for vIp = 2:Nx+1; Jp = 2:Ny+1; % Interior node numbers for piF = 2:Nx; jF = 2:Ny; % Node numbers for face flow (or advection)% Properties (air at STP)rho = 1.2; % Density (kg/m^3)mu = 1.8e-5; % Absolute viscosity (N-s/m^2)nu = mu/rho; % Kinematic viscosity (m^2/s)kt = 0.025; % Thermal conductivity (W/m-K)cp = 1006; % Specific heat (J/kg-K)alpha = kt/(rho*cp); % Thermal diffusivity (m^2/s)Pr = nu/alpha; % Prandtl number% Boundary conditionsRe = 100; % Reynolds numberU = Re*nu/(2*H); % Average velocity(m/s)Ti = 20; % Inlet temperature (deg. C)Tw = 100; % Wall temperature (deg. C)qw = 100; % Wall heat flux (W/m^2)BC_N = 1; % BC_N = 0 for Tw, BC_N = 1 for qwBC_S = 1; % BC_S = 0 for Tw, BC_S = 1 for symmetry% Solution controlsalphaU = 0.3; % Velocity relaxation (under)alphaP = 0.2; % Pressure relaxation (under)NmaxSIM = 1e+4; % Iteration max for SIMPLE algorithm (-)NmaxGSI = 1e+1; % Iteration max for numerical method (-)err = 1e-5; % Convergence criteria (-)div = 1e+1; % Divergence criteria (-)% Initialize u, v, p, T, F, a, and residual matricesu = zeros(Nx+1,Ny+2); v = zeros(Nx+2,Ny+1);uStar = zeros(Nx+1,Ny+2); vStar = zeros(Nx+2,Ny+1);uPrime = zeros(Nx+1,Ny+2); vPrime = zeros(Nx+2,Ny+1);dU = zeros(Nx+1,Ny+2); dV = zeros(Nx+2,Ny+1);T = zeros(Nx+2,Ny+2);p = zeros(Nx+2,Ny+2);pPrime = zeros(Nx+2,Ny+2);Fe = zeros(Nx+1,Ny+1); Fw = zeros(Nx+1,Ny+1); % Flow coefficientsFn = zeros(Nx+1,Ny+1); Fs = zeros(Nx+1,Ny+1);DF = zeros(Nx+1,Ny+1);aE = zeros(Nx+1,Ny+1); aW = zeros(Nx+1,Ny+1); % Coefficients foraN = zeros(Nx+1,Ny+1); aS = zeros(Nx+1,Ny+1); % discretized equationsaP = zeros(Nx+1,Ny+1); bP = zeros(Nx+1,Ny+1);ures = zeros(NmaxSIM,1); % Residual for uvres = zeros(NmaxSIM,1); % Residual for vpres = zeros(NmaxSIM,1); % Residual for pPrime% Inlet velocity for uniform flow at inletu(:,Ju) = U;% Initialize to inear pressure drop for fully developed flowp1 = 12*mu*U*L/(2*H)^2;p(Ip,Jp) = ones(Nx,Ny).*linspace(p1,0,Nx)';% Initialize temperature to inlet and wall temperaturesT(:,Jp) = Ti; T(:,1) = Tw; T(:,Ny+2) = Tw;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% SIMPLE algorithm% Constant diffussion coefficientsDx = (mu/dx)*dy*dz;Dy = (mu/dy)*dx*dz;for n = 1:NmaxSIM% Initial guessuOld = u;vOld = v;pStar = p;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% STEP 1a: solve x-momentum as uStar% Setup coefficientsFVM_u(Nx,Ny,dx,dy,dz,rho,Dx,Dy,iF,Ju,alphaU,uOld,vOld,pStar,BC_S);% Use previous calculation as initial guess in numerical method[uStar,ures(n)] = FVM_GS_ext_mesh(Nx,Ny+1,alphaU,NmaxGSI,err,uOld);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% STEP 1b: solve y-momentum as vStar% Setup coefficientsFVM_v(Nx,Ny,dx,dy,dz,rho,Dx,Dy,Iv,jF,alphaU,u,v,pStar)% Use previous calculation as initial guess in numerical method[vStar,vres(n)] = FVM_GS_ext_mesh(Nx+1,Ny,alphaU,NmaxGSI,err,vOld);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% STEP 2: Solve pressure correction equation (PCE)% Setup coefficientsFVM_pcorr(Nx,Ny,dx,dy,dz,rho,Ip,Jp,uStar,vStar)% Use numerical method to calculate pressure correctionpPrime(:,:) = 0;[pPrime,pres(n)] = FVM_GS_ext_mesh(Nx+1,Ny+1,1,NmaxGSI,err,pPrime);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% STEP 3: calculate corrected pressure and velocity% p corrections with under-relaxationp(Ip,Jp) = pStar(Ip,Jp) + pPrime(Ip,Jp)*alphaP;% u correctionsuPrime(iF,Ju) = dU(iF,Ju).*(pPrime(iF,Ju) - pPrime(iF+1,Ju));u(iF,Ju) = uStar(iF,Ju) + uPrime(iF,Ju);% v correctionsvPrime(Iv,jF) = dV(Iv,jF).*(pPrime(Iv,jF) - pPrime(Iv,jF+1));v(Iv,jF) = vStar(Iv,jF) + vPrime(Iv,jF);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% STEP 4: Check for convergence or divergenceif n > 10fprintf('n = %5.0f, u = %6.2e, v = %6.2e, p = %6.2e \n',...n,ures(n),vres(n),pres(n))cTest = max([ures(n),vres(n)]);if cTest < errbreak;elseif cTest > div || isnan(cTest)fprintf('Residuals are too high.')break;endend% Apply right boundary condition (outlet, du/dx = dv/dx = 0)u(Nx+1,:) = u(Nx,:);v(Nx+2,:) = v(Nx+1,:);end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% STEP 5: solve for temperature distribution% Setup coefficientsFVM_phi(Nx,Ny,dx,dy,dz,rho,kt/cp,qw/cp,Ip,Jp,u,v,BC_S,BC_N)% Use numerical method to calculate temperature[T,Tres] = FVM_GS_ext_mesh(Nx+1,Ny+1,1.0,1e4,1e-8,T);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% POST PROCESSINGfigure('Name','Convergence Plot for Scaled Residuals',...'Position',[100 100 500 300])% Convergence plotnlist = 10:n;semilogy(nlist,ures(nlist),'-b',nlist,vres(nlist),'-r',...nlist,pres(nlist),'-g')legend('u residual','v residual','p residual')xlabel('Iteration')ylabel('Scaled Residual')FVM_Vplot(Nx,Ny,x,xu,y,H,u(iu,Ju),v(Iv,jv),p(Ip,Jp),U)FVM_Tplot(Nx,Ny,x,y,L,H,rho,cp,u(iu,Ju),T(Ip,Jp),U,Ti,Tw,qw,BC_N)
❤️ 运行结果
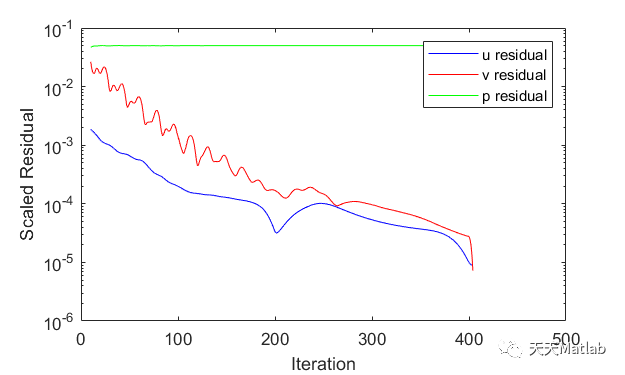
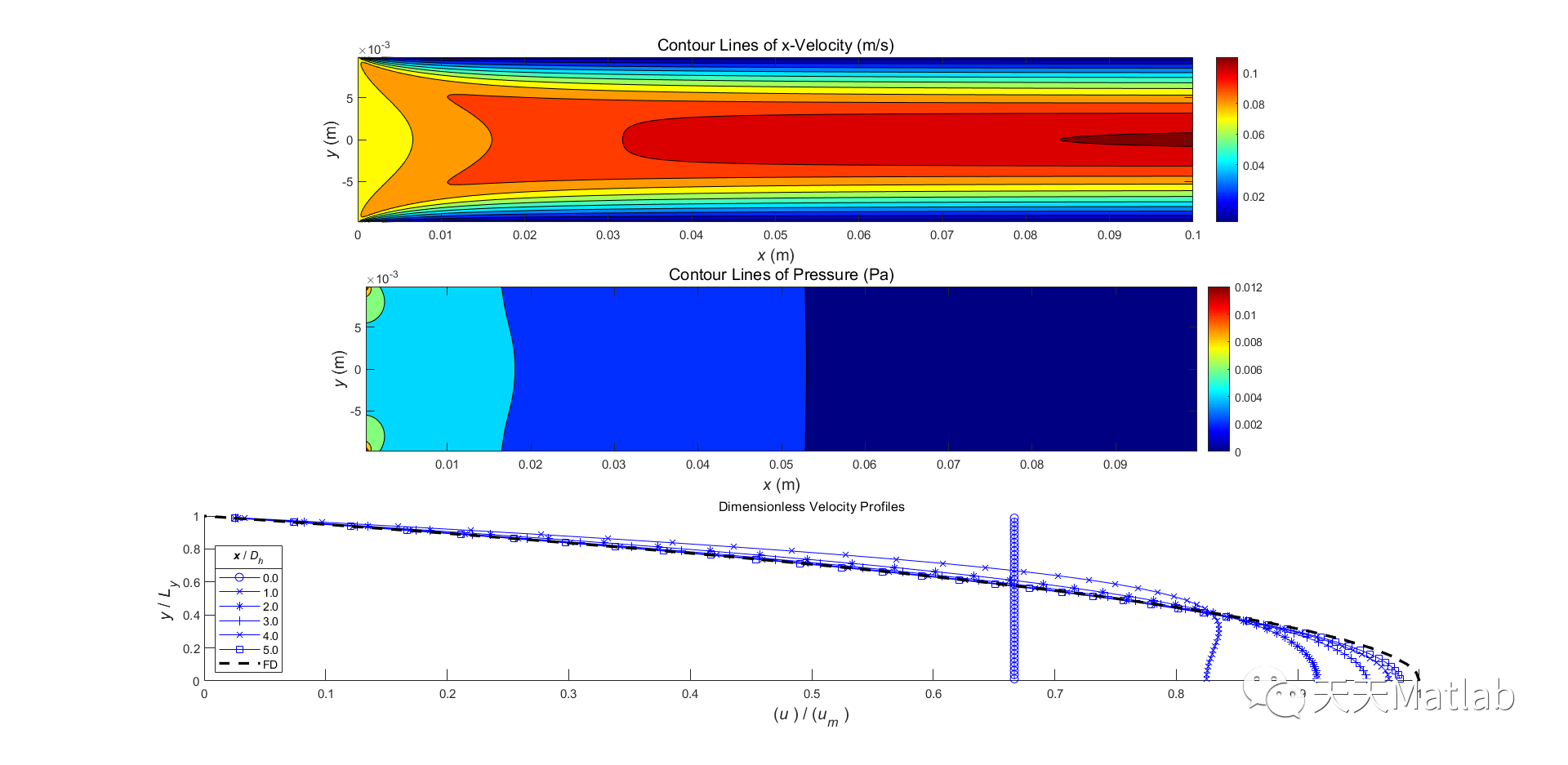
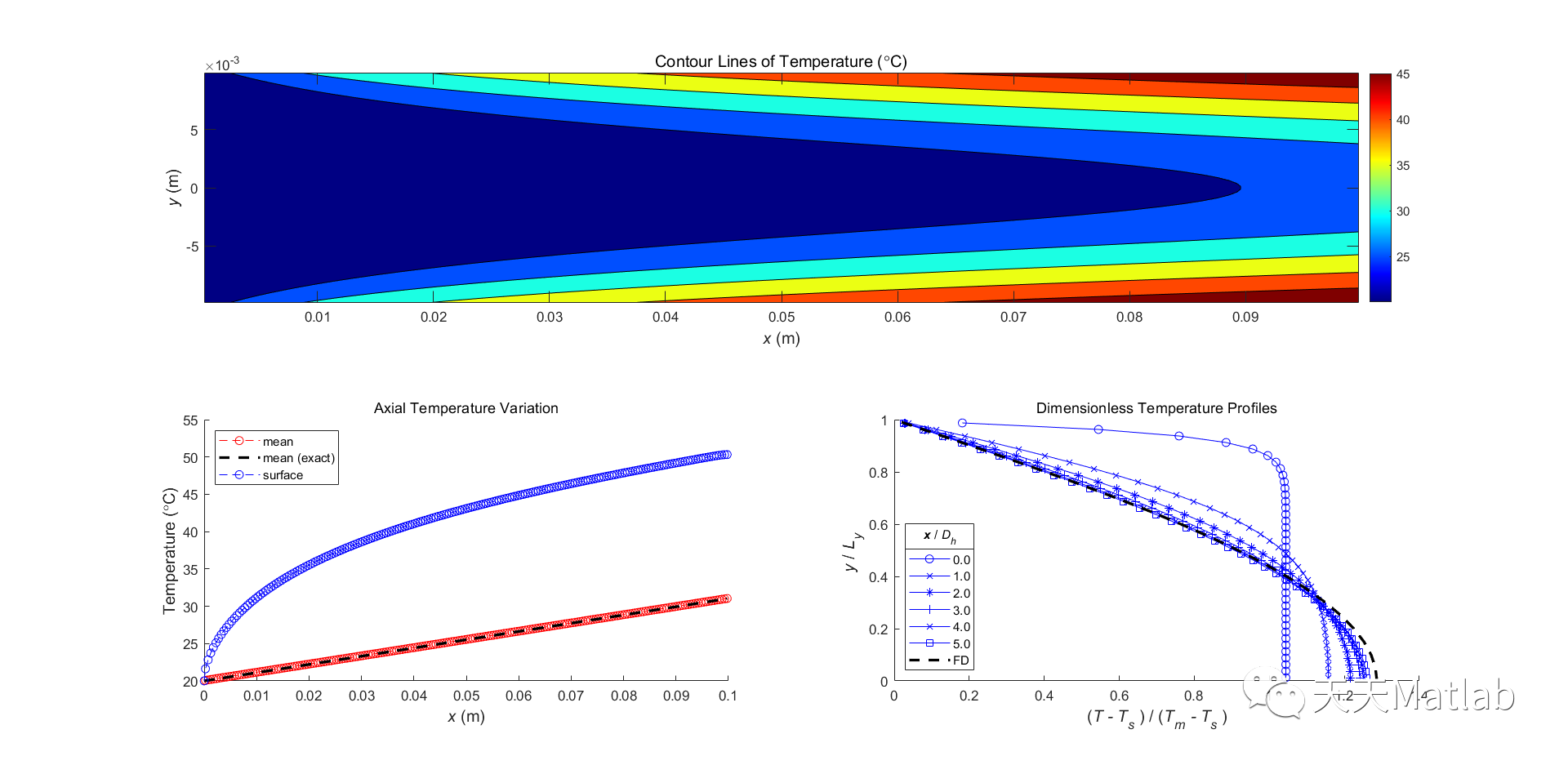
⛄ 参考文献
[1]娄淑梅,赵国群,王锐.铝型材非稳态挤压有限体积法模拟关键技术研究与应用[J].中国机械工程, 2006(S1):4.DOI:JournalArticle/5aed8a4bc095d710d40d2617.