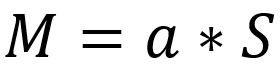文章目录
- 三、系统的数学描述
- 3.2 输入输出描述
- 二、初始松弛概念
- 三、线性性质
- 四、因果律
- 五、松驰性
- 六、时不变性
- 七、传递函数阵
- 小结
- 3.3 状态变量描述
- 3.4 输入输出描述和状态变量描述的关系
- 3.5 组合系统的数学描述
- 一、时变情形
- 二、时不变情形
- 四、线性动态方程和脉冲响应矩阵
- 4.2 线性动态方程的解
- 一、齐次方程的解
- 二、基本矩阵和状态转移矩阵
- 三、非齐次方程的解
- 4.3 等价动态方程
- 一、时不变系统的等价动态方程
- 三、经等价变换之后的基本矩阵和状态转移矩阵
- 四、具有周期的线性时变动态方程
- 4.4 脉冲响应矩阵与动态方程
- 一、由动态方程到输入/输出描述
- 二、由输入/输出描述到动态方程(时变系统)
- 三、由输入/输出描述到动态方程(时不变系统)
- 五、线性动态方程的可控性和可观测性
- 5.1 引言
- 5.2 时间函数的线性无关性
- 二、Gram矩阵
- 二、一些有用的判别准则
- 5.3 线性动态方程的可控性
- 一、可控性的定义及判别定理
- 二、时不变系统可控性判据
- 三、时不变系统的振型(模态)、模式
- 四、简化的可控性条件
- 5.4 线性动态方程的可观测性
- 一、可观测性定义
- 二、可观测性的一般判别准则
- 三、可重构性
- 四、线性系统的对偶性
- 五、线性时不变系统的可观测性判据
- 5.5 线性时不变系统的规范分解
- 一、等价变换的性质
- 二、动态方程按可控性分解
- 三、动态方程的可观性分解
- 四、规范分解定理
- 五、不可简约的动态方程
- 5.6 约当形(若当)动态方程的可控性和可观测性
- 5.7 输出可控性
- 5.8.4 连续系统时间离散化后保持可控和可观测条件
- 六、不可简约实现
- 6.1 引言
- 6.2 正则有理矩阵的特征多项式和次数
- 6.3 正则有理函数的不可简约实现
- 一、单变量系统
- 二、多变量系统的标准形
- 三、正则有理传递函数的最小实现
- 6.4 多变量系统的实现
- 一、动态方程的可控性、可观性与传递函数阵之间的关系
- 二、向量传递函数的实现
- 三、传递函数矩阵G(s)的实现
- 七、状态反馈和状态观测器
- 7.2 状态反馈
- 一、状态反馈对可控可观的影响
- 二、输出反馈对可控可观的影响
- 三、单输入系统的极点配置
- 四、状态反馈对传递函数零点的影响
- 七、镇定问题
- 7.3 状态观测器
- 二、状态观测器的存在性、n为状态观测器
- 三、单输入单输出系统的状态观测器
- 五、最小维状态观测器
- 7.4 状态反馈与状态观测器的连接
- 一、包括观测器的状态反馈系统的构成
- 二、包括观测器的状态反馈系统的特性
- 八、线性系统的稳定性
- 8.1 李氏稳定
- 8.2 线性时不变系统的稳定性分析
- 三、总体稳定(T稳定)
- 关系图
三、系统的数学描述
3.2 输入输出描述
二、初始松弛概念
瞬时系统(无记忆系统):t1时刻的输出仅仅取决于该时刻所加的输入(仅由电阻构成的网络)
系统在t1时刻松弛:在t1时刻系统不存储能量
三、线性性质
1、定义
系统是线性的判别: H ( α 1 u 1 + α 2 u 2 ) = α 1 H u 1 + α 2 H u 2 \mathbf{H}\left(\alpha_{1} u_{1}+\alpha_{2} u_{2}\right)=\alpha_{1} H u_{1}+\alpha_{2} H u_{2} H(α1u1+α2u2)=α1Hu1+α2Hu2(可加性和齐次性)
2、线性松弛系统的脉冲响应
脉冲函数: δ Δ ( t − t 1 ) = { 0 , t < t 1 1 Δ , t 1 ≤ t < t 1 + Δ 0 , t > t 1 + Δ \delta_{\Delta}\left(t-t_{1}\right)=\left\{\begin{array}{ll} 0, & t<t_{1} \\ \frac{1}{\Delta}, & t_{1} \leq t<t_{1}+\Delta \\ 0, & t>t_{1}+\Delta \end{array}\right. δΔ(t−t1)=⎩ ⎨ ⎧0,Δ1,0,t<t1t1≤t<t1+Δt>t1+Δ
用脉冲函数近似表示信号: u ≅ ∑ u ( t i ) δ Δ ( t − t i ) Δ u \cong \sum u\left(t_{i}\right) \delta_{\Delta}\left(t-t_{i}\right) \Delta u≅∑u(ti)δΔ(t−ti)Δ
3、线性系统y=Hu的脉冲响应函数
级数变成积分的形式: y = H u = H ∑ u ( t i ) δ Δ ( t − t i ) Δ = ∫ − ∞ + ∞ [ H δ ( t − τ ) ] u ( τ ) d τ y=Hu=H\sum u\left(t_{i}\right) \delta_{\Delta}\left(t-t_{i}\right) \Delta=\int_{-\infty}^{+\infty}[H \delta(t-\tau)] u(\tau) d \tau y=Hu=H∑u(ti)δΔ(t−ti)Δ=∫−∞+∞[Hδ(t−τ)]u(τ)dτ
系统脉冲响应函数: H δ ( t − τ ) = g ( t , τ ) H \delta(t-\tau)=g(t,\tau) Hδ(t−τ)=g(t,τ)
4、脉冲响应矩阵
由系统脉冲响应函数组成的矩阵,其中 g i j ( t , τ ) g_{ij}(t,\tau) gij(t,τ)是第i个输出端对第j个输入端的脉冲响应
四、因果律
因果的(非预期的):若系统在时刻t 的输出只取决于时刻t和在t之前的输入 y ( t ) = H u ( − ∞ , t ) y(t)=H u_{(-\infty, t)} y(t)=Hu(−∞,t)
五、松驰性
系统在 t 0 t_0 t0时刻是松弛的:当且仅当系统输出 y ( t 0 , ∞ ) \mathrm{y}\left(\mathrm{t}_{0}, \infty\right) y(t0,∞)唯一的由 u ( t 0 , ∞ ) \mathrm{u}\left(\mathrm{t}_{0}, \infty\right) u(t0,∞)所激励 y ( t 0 , + ∞ ) = H u ( t 0 , ∞ ) y_{\left(t_{0},+\infty\right)}=H u_{\left(t_{0}, \infty\right)} y(t0,+∞)=Hu(t0,∞)
六、时不变性
1、时不变系统的定义
系统是时不变的:输入信号延迟 α \alpha α秒,其响应也恰好延迟 α \alpha α秒,且波形不变 u ˉ ( t ) = Q α u ( t ) = u ( t − α ) \bar{u}(t)=Q_{\alpha} u(t)=u(t-\alpha) uˉ(t)=Qαu(t)=u(t−α)
2、时不变、线性、松弛系统的脉冲响应函数
g ( t , τ ) = H δ ( t − τ ) = g ( t − τ , 0 ) = g ( t − τ ) g(t,\tau)=H \delta(t-\tau)=g(t-\tau,0)=g(t-\tau) g(t,τ)=Hδ(t−τ)=g(t−τ,0)=g(t−τ)
七、传递函数阵
4、正则和严格正则
正则: g ( ∞ ) g(\infty) g(∞)是有限常量
严格正则: g ( ∞ ) = 0 g(\infty)=0 g(∞)=0
小结

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eDfLZqWb-1670243541441)(C:\Users\91996\AppData\Roaming\Typora\typora-user-images\image-20221128161945924.png)]](https://img-blog.csdnimg.cn/c98aba952bf24ef2b0da17151f4a5363.png)
3.3 状态变量描述
如果用能量的概念,可以把系统的运动过程看作是能量的变换过程,因此状态变量的数目等于且仅仅等于系统中包含独立贮能元件的数目;
3.4 输入输出描述和状态变量描述的关系
二、由输入输出导出状态空间描述
传递函数: g ( s ) = y ( s ) u ( s ) = b m s m + b m − 1 s m − 1 + … … + b 1 s 1 + b 0 s n + a n − 1 s n − 1 + … … + a 1 s 1 + a 0 s g(s)=\frac{y(s)}{u(s)}=\frac{b_{m} s^{m}+b_{m-1} s^{m-1}+\ldots \ldots+b_{1} s^{1}+b_{0}}{s^{n}+\mathrm{a}_{\mathrm{n}-1} s^{n-1}+\ldots \ldots+a_{1} s^{1}+a_{0} s} g(s)=u(s)y(s)=sn+an−1sn−1+……+a1s1+a0sbmsm+bm−1sm−1+……+b1s1+b0
状态变量: x ˙ = [ 0 1 ⋮ ⋱ 0 1 − a 0 − a 1 − a n − 1 ] x + [ 0 ⋮ 0 1 ] u y = [ b 0 , ⋯ , b m , 0 , ⋯ , 0 ] x \begin{array}{l} \dot{x}=\left[\begin{array}{lrrr} 0 & 1 & & \\ \vdots & & \ddots & \\ 0 & & & 1 \\ -a_{0} & -a_{1} & & -a_{n-1} \end{array}\right] x+\left[\begin{array}{l} 0 \\ \vdots \\ 0 \\ 1 \end{array}\right] u \\ y=\left[b_{0}, \cdots, b_{m}, 0, \cdots, 0\right] x \end{array} x˙= 0⋮0−a01−a1⋱1−an−1 x+ 0⋮01 uy=[b0,⋯,bm,0,⋯,0]x
三、由方框图描述导出状态空间描述
1、化简方框图成规范方框图(各组成环节只为一阶惯性环节和比例放大环节)
2、指定状态变量,列些关系方程
四、由状态空间描述导出传递函数矩阵
G ( s ) = C ( s I − A ) − 1 B + E \mathbf{G}(s)=\mathbf{C}(s \mathbf{I}-\mathbf{A})^{-1} \mathbf{B}+E G(s)=C(sI−A)−1B+E
3.5 组合系统的数学描述
一、时变情形
1、组合系统的输入输出描述
两个多变量系统 S i S_i Si由下式描述: y i ( t ) = ∫ − ∞ t G i ( t , τ ) u i ( τ ) d τ i = 1 , 2 y_{i}(t)=\int_{-\infty}^{t} G_{i}(t, \tau) u_{i}(\tau) d \tau \quad i=1,2 yi(t)=∫−∞tGi(t,τ)ui(τ)dτi=1,2
并联系统: G ( t , τ ) = G 1 ( t , τ ) + G 2 ( t , τ ) G(t, \tau)=G_{1}(t, \tau)+G_{2}(t, \tau) G(t,τ)=G1(t,τ)+G2(t,τ)
串联系统: G ( t , τ ) = ∫ τ t G 2 ( t , ν ) G 1 ( ν , τ ) d ν G(t, \tau)=\int_{\tau}^{t} G_{2}(t, \nu) G_{1}(\nu, \tau) d \nu G(t,τ)=∫τtG2(t,ν)G1(ν,τ)dν
反馈系统: G ( t , τ ) = G 1 ( t , τ ) − ∫ τ t G 1 ( t , τ ) ∫ τ ν G 2 ( ν , s ) G ( s , τ ) d s d ν G(t, \tau)=G_{1}(t, \tau)-\int_{\tau}^{t} G_{1}(t, \tau) \int_{\tau}^{\nu} G_{2}(\nu, s) G(s, \tau) d s d \nu G(t,τ)=G1(t,τ)−∫τtG1(t,τ)∫τνG2(ν,s)G(s,τ)dsdν
2、组合系统的状态变量描述
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rPvxkQTs-1670243541441)(C:\Users\91996\AppData\Roaming\Typora\typora-user-images\image-20221128165436751.png)]](https://img-blog.csdnimg.cn/f34e4f59ac6e42fa91f1e6ad16ab6fff.png)

二、时不变情形
1、组合系统的传递函数
并联系统: G ( S ) = G 1 ( S ) + G 2 ( S ) G(S)=G_1(S)+G_2(S) G(S)=G1(S)+G2(S)
串联系统: G ( S ) = G 1 ( S ) ∗ G 2 ( S ) G(S)=G_1(S)*G_2(S) G(S)=G1(S)∗G2(S)
反馈系统: G ( s ) = G 1 ( s ) ( I p + G 2 ( s ) G 1 ( s ) ) − 1 = ( I q + G 1 ( s ) G 2 ( s ) ) − 1 G 1 ( s ) G(s)=G_{1}(s)\left(I_{p}+G_{2}(s) G_{1}(s)\right)^{-1}=\left(I_{q}+G_{1}(s) G_{2}(s)\right)^{-1} G_{1}(s) G(s)=G1(s)(Ip+G2(s)G1(s))−1=(Iq+G1(s)G2(s))−1G1(s)(其中 d e t ( I q + G 1 ( s ) G 2 ( s ) ) ≠ 0 det\left(I_{q}+G_{1}(s) G_{2}(s)\right)≠0 det(Iq+G1(s)G2(s))=0)
注意: det ( I + E 1 E 2 ) ≠ 0 ⇀ d e t ( I q + G 1 ( s ) G 2 ( s ) ) ≠ 0 \operatorname{det}\left(I+E_{1} E_{2}\right) \neq 0\rightharpoonup det\left(I_{q}+G_{1}(s) G_{2}(s)\right)≠0 det(I+E1E2)=0⇀det(Iq+G1(s)G2(s))=0
2、适定性问题
判别系统是正则的:
传递函数矩阵中的 [ I q + G 1 ( ∞ ) G 2 ( ∞ ) ] \left[\mathrm{I}_{\mathrm{q}}+\mathrm{G}_{1}(\infty) \mathrm{G}_{2}(\infty)\right] [Iq+G1(∞)G2(∞)]是非奇异的,则 G ( s ) = G 1 ( s ) ( I p + G 2 ( s ) G 1 ( s ) ) − 1 G(s)=G_{1}(s)\left(I_{p}+G_{2}(s) G_{1}(s)\right)^{-1} G(s)=G1(s)(Ip+G2(s)G1(s))−1是正则的
注意:
这里 [ I q + G 1 ( ∞ ) G 2 ( ∞ ) ] \left[\mathrm{I}_{\mathrm{q}}+\mathrm{G}_{1}(\infty) \mathrm{G}_{2}(\infty)\right] [Iq+G1(∞)G2(∞)]和 [ I q + G 2 ( ∞ ) G 1 ( ∞ ) ] \left[\mathrm{I}_{\mathrm{q}}+\mathrm{G}_{2}(\infty) \mathrm{G}_{1}(\infty)\right] [Iq+G2(∞)G1(∞)]非奇异与状态变量描述时的条件 ( I + E 1 E 2 ) \left(I+E_{1} E_{2}\right) (I+E1E2)非奇异是相同的
组合系统是适定的:
每个子系统是正则的,从任意作为输入端的点至沿着邮箱路径的每一个其他的闭环传递函数存在且正则
举例:
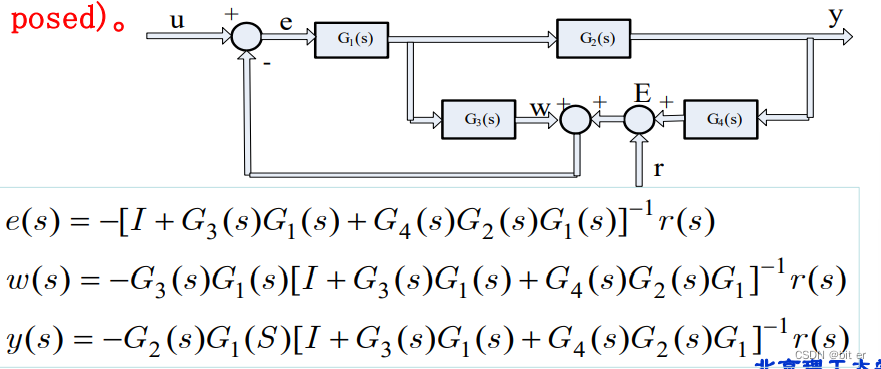
判别条件:当且仅当系统不具有在 s = ∞ s=\infty s=∞时其纯回路增益为"1"的组合回路(不会有重合顶点),系统才是适定的。
四、线性动态方程和脉冲响应矩阵
4.2 线性动态方程的解
输入-输出描述方程的解: y ( t ) = ∫ t 0 t G ( t , τ ) u ( τ ) d τ y(t)=\int_{t_{0}}^{t} G(t, \tau) u(\tau) d \tau y(t)=∫t0tG(t,τ)u(τ)dτ
一、齐次方程的解
解的存在和唯一性:由初值条件的方程,只能有一个解满足
Ψ ˙ ( t ) = A ( t ) Ψ ( t ) \dot{\mathbf{\Psi}}(t)=\mathbf{A}(t) \boldsymbol{\Psi}(t) Ψ˙(t)=A(t)Ψ(t)
方程 d x d t = A ( t ) x \frac{dx}{dt}=A(t)x dtdx=A(t)x的所有解的集合,形成在实数域上的n维向量空间
二、基本矩阵和状态转移矩阵
1、基本矩阵
定义(不唯一):
[ Ψ 1 ( t ) Ψ 2 ( t ) ⋯ Ψ n ( t ) ] = Ψ ( t ) , t ∈ ( − ∞ , + ∞ ) \left[\begin{array}{llll} \boldsymbol{\Psi}^{1}(t) & \boldsymbol{\Psi}^{2}(t) & \cdots & \boldsymbol{\Psi}^{n}(t) \end{array}\right]=\boldsymbol{\Psi}(t), t \in(-\infty,+\infty) [Ψ1(t)Ψ2(t)⋯Ψn(t)]=Ψ(t),t∈(−∞,+∞)其中 Ψ i ( t ) \Psi^{i}(t) Ψi(t)是 x ˙ ( t ) = A ( t ) x ( t ) \dot{x}(t)=\mathbf{A}(t) x(t) x˙(t)=A(t)x(t)的n个线性无关解
性质:
方程 x ˙ ( t ) = A ( t ) x ( t ) \dot{x}(t)=\mathbf{A}(t) x(t) x˙(t)=A(t)x(t)的基本矩阵对于 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)中的所有t均为非奇异矩阵
2、状态转移矩阵
定义:
Ψ ( t ) \Psi(t) Ψ(t)是 x ˙ ( t ) = A ( t ) x ( t ) \dot{x}(t)=\mathbf{A}(t) x(t) x˙(t)=A(t)x(t)的基本矩阵,则 Φ ( t , t 0 ) = Ψ ( t ) Ψ − 1 ( t 0 ) \boldsymbol{\Phi}\left(t, t_{0}\right)=\boldsymbol{\Psi}(t) \boldsymbol{\Psi}^{-1}\left(t_{0}\right) Φ(t,t0)=Ψ(t)Ψ−1(t0)是对应的状态转移矩阵
主要性质:
① Φ ( t , t ) = I \mathbf{\mathbf { \Phi }}(t, t)=\mathbf{I} Φ(t,t)=I
② d Φ ( t , t 0 ) d t = A ( t ) Φ ( t , t 0 ) \frac{d \mathbf{\Phi}\left(t, t_{0}\right)}{d t}=\mathbf{A}(t) \mathbf{\Phi}\left(t, t_{0}\right) dtdΦ(t,t0)=A(t)Φ(t,t0)(利用了 Ψ ˙ ( t ) = A ( t ) Ψ ( t ) \dot{\mathbf{\Psi}}(t)=\mathbf{A}(t) \boldsymbol{\Psi}(t) Ψ˙(t)=A(t)Ψ(t))
③ x ( t ) = Φ ( t , t 0 ) x 0 \mathbf{x}(t)=\mathbf{\Phi}\left(t, t_{0}\right) \mathbf{x}_{0} x(t)=Φ(t,t0)x0( x ( t ) = Ψ ( t ) α \mathbf{x}(t)=\boldsymbol{\Psi}(t) \boldsymbol{\alpha} x(t)=Ψ(t)α表示)
④ Φ ( t , t 0 ) \mathbf{\Phi}\left(t, t_{0}\right) Φ(t,t0)由 A ( t ) A(t) A(t)唯一确定,与 Ψ ( t ) \Psi(t) Ψ(t)无关
三、非齐次方程的解
1、时变线性系统的解
根据 x ˙ = A ( t ) x + B ( t ) u x ( t 0 ) = x 0 \begin{array}{l} \dot{\mathbf{x}}=\mathbf{A}(t) \mathbf{x}+\mathbf{B}(t) \mathbf{u} \\ \mathbf{x}\left(t_{0}\right)=\mathbf{x}_{0} \end{array} x˙=A(t)x+B(t)ux(t0)=x0可以求状态方程的解为 x ( t ) = Φ ( t , t 0 ) x 0 + ∫ t 0 t Φ ( t , τ ) B ( τ ) u ( τ ) d τ \mathbf{x}(t)=\Phi\left(t, t_{0}\right) \mathbf{x}_{0}+\int_{t_{0}}^{t} \Phi(t, \tau) \mathbf{B}(\tau) \mathbf{u}(\tau) d \tau x(t)=Φ(t,t0)x0+∫t0tΦ(t,τ)B(τ)u(τ)dτ
其中 Φ ( t , t 0 ) x 0 \Phi\left(t, t_{0}\right) \mathbf{x}_{0} Φ(t,t0)x0是零输入响应, ∫ t 0 t Φ ( t , τ ) B ( τ ) u ( τ ) d τ \int_{t_{0}}^{t} \Phi(t, \tau) \mathbf{B}(\tau) \mathbf{u}(\tau) d \tau ∫t0tΦ(t,τ)B(τ)u(τ)dτ是零状态响应
2、输入输出关系
动态方程的输出为: y ( t ) = C ( t ) x ( t ) + E ( t ) u ( t ) = C ( t ) ( Φ ( t , t 0 ) x 0 + ∫ t 0 t Φ ( t , τ ) B ( τ ) u ( τ ) d τ ) + E ( t ) u ( t ) y(t)=C(t)x(t)+E(t)u(t)=C(t)(\Phi\left(t, t_{0}\right) \mathbf{x}_{0}+\int_{t_{0}}^{t} \Phi(t, \tau) \mathbf{B}(\tau) \mathbf{u}(\tau) d \tau)+E(t)u(t) y(t)=C(t)x(t)+E(t)u(t)=C(t)(Φ(t,t0)x0+∫t0tΦ(t,τ)B(τ)u(τ)dτ)+E(t)u(t)
当 x ( t 0 ) = 0 x(t_0)=0 x(t0)=0,可以得到脉冲响应矩阵:
t ≥ τ : G ( t , τ ) = C ( t ) Φ ( t , τ ) B ( τ ) + E ( t ) δ ( t − τ ) t \geq \tau: \quad \mathbf{G}(t, \tau)=\mathbf{C}(t) \Phi(t, \tau) \mathbf{B}(\tau)+E(t) \delta(t-\tau) t≥τ:G(t,τ)=C(t)Φ(t,τ)B(τ)+E(t)δ(t−τ)
t < τ : G ( t , τ ) = 0 t<\tau: \quad \mathbf{G}(t, \tau)=0 t<τ:G(t,τ)=0
3、线性时不变动态方程的解
基本矩阵变成: e A t e^{At} eAt,状态转移矩阵变成:$\mathbf{\Phi}\left(t- t_{0}\right) $
此时动态方程的解为:
x ( t ) = e A ( t − t 0 ) x 0 + ∫ t 0 t e A ( t − τ ) B u ( τ ) d τ \mathbf{x}(t)=e^{\mathbf{A}\left(t-t_{0}\right)} \mathbf{x}_{0}+\int_{t_{0}}^{t} e^{\mathbf{A}(t-\tau)} \mathbf{B u}(\tau) d \tau x(t)=eA(t−t0)x0+∫t0teA(t−τ)Bu(τ)dτ
y ( t ) = C e A ( t − t 0 ) x 0 + ∫ t 0 t C e A ( t − τ ) B u ( τ ) d τ + E u ( t ) \mathbf{y}(t)=\mathbf{C} e^{\mathbf{A}\left(t-t_{0}\right)} \mathbf{x}_{0}+\int_{t_{0}}^{t} \mathbf{C} e^{\mathbf{A}(t-\tau)} \mathbf{B u}(\tau) d \tau+E \mathbf{u}(t) y(t)=CeA(t−t0)x0+∫t0tCeA(t−τ)Bu(τ)dτ+Eu(t)
对应的脉冲响应矩阵变为:
t ≥ τ G ( t − τ ) = C e A ( t − τ ) B + E δ ( t − τ ) t \geq \tau \quad \mathbf{G}(t-\tau)=\mathbf{C} e^{\mathbf{A}(t-\tau)} \mathbf{B}+E \delta(t-\tau) t≥τG(t−τ)=CeA(t−τ)B+Eδ(t−τ)
t < τ G ( t , τ ) = 0 t<\tau \quad \mathbf{G}(t, \tau)=0 t<τG(t,τ)=0
4、线性时不变基本矩阵的性质和求法
性质: lim t → 0 e A t = I \lim _{t \rightarrow 0} e^{\mathbf{A} t}=I limt→0eAt=I、 d d t e A t = A e A t = e A t A \frac{d}{d t} e^{\mathbf{A} t}=A e^{\mathbf{A} t}=e^{\mathbf{A} t} A dtdeAt=AeAt=eAtA
求法:利用 s I − A sI-A sI−A的逆来求解
4.3 等价动态方程
一、时不变系统的等价动态方程
①由 x ‾ = P x \overline{\mathbf{x}}=\mathbf{P} \mathbf{x} x=Px产生的 A ‾ = P A P − 1 \overline{\mathbf{A}}=\mathbf{P A} \mathbf{P}^{-1} A=PAP−1、 B ‾ = P B \overline{\mathbf{B}}=\mathbf{P B} B=PB、 C ‾ = C P − 1 \overline{\mathbf{C}}=\mathbf{C P}^{-1} C=CP−1、 E ˉ = E \bar{E}=E Eˉ=E。其中P为非奇异矩阵
零状态等价:相同的脉冲响应矩阵和传递函数矩阵
零输入等价:相同的零输入响应
②两个动态方程维数和传递函数阵相同$\leftharpoonup 动态方程等价 动态方程等价 动态方程等价\rightharpoonup $零输入和零状态等价
③两个维数不一定相同的线性时不变动态方程具有相同的传递函数的充要条件是: E ˉ = E \bar{E}=E Eˉ=E、 C A i B = C ‾ A i ‾ B ‾ \mathbf{C A}^{\mathbf{i}} \mathbf{B}=\overline{\mathbf{C}} \overline{\mathbf{A}^{\mathbf{i}}} \overline{\mathbf{B}} CAiB=CAiB
二、时变系统的等价动态方程
由 x ‾ ( t ) = P ( t ) x ( t ) \overline{\mathbf{x}}(t)=\mathbf{P}(t) \mathbf{x}(t) x(t)=P(t)x(t)产生的 A ‾ ( t ) = [ P ( t ) A ( t ) + P ˙ ( t ) ] P − 1 ( t ) \overline{\mathbf{A}}(t)=[\mathbf{P}(t) \mathbf{A}(t)+\dot{\mathbf{P}}(t)] \mathbf{P}^{-\mathbf{1}}(t) A(t)=[P(t)A(t)+P˙(t)]P−1(t)、 B ‾ ( t ) = P ( t ) B ( t ) \overline{\mathbf{B}}(t)=\mathbf{P}(t) \mathbf{B}(t) B(t)=P(t)B(t)、 C ‾ ( t ) = C ( t ) P − 1 ( t ) \overline{\mathbf{C}}(t)=\mathbf{C}(t) \mathbf{P}^{-1}(t) C(t)=C(t)P−1(t)、 E ( t ) ˉ = E ( t ) \bar{E(t)}=E(t) E(t)ˉ=E(t)
三、经等价变换之后的基本矩阵和状态转移矩阵
基本矩阵: P ( t ) Ψ ( t ) \mathbf{P}(t) \Psi(t) P(t)Ψ(t) 状态转移矩阵: P ( t ) Φ ( t , t 0 ) P − 1 ( t 0 ) \mathrm{P}(t) \Phi\left(t, t_{0}\right) \mathrm{P}^{-1}\left(t_{0}\right) P(t)Φ(t,t0)P−1(t0)
四、具有周期的线性时变动态方程
4.4 脉冲响应矩阵与动态方程
一、由动态方程到输入/输出描述
在 x ( t 0 ) = 0 x(t_0)=0 x(t0)=0时,动态方程的解为 y ( t ) = C ( t ) ∫ t 0 t Φ ( t , τ ) B ( τ ) u ( τ ) d τ + E ( t ) u ( t ) = ∫ t 0 t ( C ( t ) Φ ( t , τ ) B ( τ ) + E ( t ) δ ( t − τ ) ) u ( τ ) d τ y(t)=C(t)\int_{t_{0}}^{t} \Phi(t, \tau) \mathbf{B}(\tau) \mathbf{u}(\tau) d \tau+E(t)u(t)=\int_{t_{0}}^{t} (\mathbf{C}(t) \Phi(t, \tau) \mathbf{B}(\tau)+E(t) \delta(t-\tau)) u(\tau) d \tau y(t)=C(t)∫t0tΦ(t,τ)B(τ)u(τ)dτ+E(t)u(t)=∫t0t(C(t)Φ(t,τ)B(τ)+E(t)δ(t−τ))u(τ)dτ
所以:
t ≥ τ : G ( t , τ ) = C ( t ) Φ ( t , τ ) B ( τ ) + E ( t ) δ ( t − τ ) t \geq \tau: \quad \mathbf{G}(t, \tau)=\mathbf{C}(t) \Phi(t, \tau) \mathbf{B}(\tau)+E(t) \delta(t-\tau) t≥τ:G(t,τ)=C(t)Φ(t,τ)B(τ)+E(t)δ(t−τ)
t < τ : G ( t , τ ) = 0 t<\tau: \quad \mathbf{G}(t, \tau)=0 t<τ:G(t,τ)=0
二、由输入/输出描述到动态方程(时变系统)
当且仅当 G ( t , τ ) \mathbf{G}(t, \tau) G(t,τ)分解为 G ( t , τ ) = M ( t ) N ( τ ) + E ( t ) δ ( t − τ ) \mathbf{G}(t, \tau)=M(t)N(\tau)+E(t) \delta(t-\tau) G(t,τ)=M(t)N(τ)+E(t)δ(t−τ)说明是状态转移矩阵是能用有限维动态方程来实现的。
三、由输入/输出描述到动态方程(时不变系统)
当 G ( s ) G(s) G(s)是正则有理函数矩阵的时候,说明 G ( s ) G(s) G(s)是可以由有限维线性动态方程来实现的
五、线性动态方程的可控性和可观测性
5.1 引言
容许控制:定义在 [ t 0 , + ∞ ) [t_0,+\infty) [t0,+∞)上连续或分段连续函数组成的控制向量
5.2 时间函数的线性无关性
二、Gram矩阵
1、定义
W ( t 1 , t 2 ) n × n = ∫ t 1 t 2 F ( t ) F ∗ ( t ) d t \mathbf{W}\left(t_{1}, t_{2}\right)_{n \times n}=\int_{t_{1}}^{t_{2}} \mathbf{F}(t) \mathbf{F}^{*}(t) d t W(t1,t2)n×n=∫t1t2F(t)F∗(t)dt其中F矩阵是由 f 1 , f 2 . . . f n f_1,f_2...f_n f1,f2...fn(1×p维)组成的矩阵
其中 f 1 , f 2 . . . f n f_1,f_2...f_n f1,f2...fn(1×p维)线性无关的充要条件是 W ( t 1 , t 2 ) n × n = ∫ t 1 t 2 F ( t ) F ∗ ( t ) d t \mathbf{W}\left(t_{1}, t_{2}\right)_{n \times n}=\int_{t_{1}}^{t_{2}} \mathbf{F}(t) \mathbf{F}^{*}(t) d t W(t1,t2)n×n=∫t1t2F(t)F∗(t)dt非奇异
二、一些有用的判别准则
①
先求矩阵各阶导,然后找存在点来判断是否线性无关(n-1阶)
缺点:很难找到某个点来满足条件,所以是充分条件
②解决的问题:难找点
先找任意点,然后求导来判断线性无关(后面由无穷多个,直到找到n阶)
5.3 线性动态方程的可控性
一、可控性的定义及判别定理
1、定义
可控定义:在 t 1 t_1 t1时刻把 x ( t 0 ) x(t_0) x(t0)转移到0
可达定义:在 [ t 0 , t 1 ] [t_0,t_1] [t0,t1]内使状态 x ( t 1 ) = 0 x(t_1)=0 x(t1)=0转移到 x ( t 0 ) x(t_0) x(t0)
2、可控的一般判别准则
状态方程在 t 0 t_0 t0可控的充要条件: Φ ( t 0 , τ ) B ( τ ) \Phi(t_{0},\tau)B(\tau ) Φ(t0,τ)B(τ)的n个行在时间内线性无关
3、从 x ( t 0 ) x(t_0) x(t0)转移到 x ( t 1 ) x(t_1) x(t1)的输入 u ( t ) u(t) u(t):
u ( t ) = − B ∗ ( t ) Φ ∗ ( t 0 , t ) W − 1 ( t 0 , t 1 ) [ x 0 − Φ ( t 0 , t 1 ) x 1 ] u(t)=-\mathbf{B} ^*(t) \mathbf{\Phi} ^*\left(t_{0}, t\right) \mathbf{W}^{-1}\left(t_{0}, t_{1}\right)\left[x_{0}-\mathbf{\Phi}\left(t_{0}, t_{1}\right) x_{1}\right] u(t)=−B∗(t)Φ∗(t0,t)W−1(t0,t1)[x0−Φ(t0,t1)x1]
4、可控性的实用判据
解决的问题:求状态转移矩阵太难了
状态方程在 t 0 t_0 t0可控的条件: r a n k [ M 0 ( t ) , M 1 ( t ) , M 2 ( t ) , . . . , M n − 1 ( t ) ] = n rank[M_0(t),M_1(t),M_2(t),...,M_{n-1}(t)]=n rank[M0(t),M1(t),M2(t),...,Mn−1(t)]=n
M 0 ( t ) = B ( t ) M_0(t)=B(t) M0(t)=B(t)、 M k ( t ) = − A ( t ) M k − 1 ( t ) + d M k − 1 ( t ) d t M_k(t)=-A(t)M_{k-1}(t)+\frac{\mathrm{d}M_{k-1}(t)}{\mathrm{d} t} Mk(t)=−A(t)Mk−1(t)+dtdMk−1(t)
n维方程在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)对每一个t均微分可控的充要条件是: r a n k [ M 0 ( t 0 ) , M 1 ( t 0 ) , M 2 ( t 0 ) , . . . , M n − 1 ( t 0 ) , . . . ] = n rank[M_0(t_0),M_1(t_0),M_2(t_0),...,M_{n-1}(t_0),...]=n rank[M0(t0),M1(t0),M2(t0),...,Mn−1(t0),...]=n
二、时不变系统可控性判据
1、七条判据:AB判据、PBH判据
三、时不变系统的振型(模态)、模式
1、定义
振型(模态):矩阵A的特征值
模式: x ˙ = A x + B u \dot x=Ax+Bu x˙=Ax+Bu
可控振型:PBH判据
四、简化的可控性条件
如果 r a n k B = r rankB=r rankB=r,则 ( A , B ) (A,B) (A,B)可控的充要条件是 r a n k U n − r = r a n k [ B A B . . . A n − r B ] = n rankU_{n-r}=rank[B\quad AB ... \quad A^{n-r}B]=n rankUn−r=rank[BAB...An−rB]=n
可控性指数是:j+1
5.4 线性动态方程的可观测性
一、可观测性定义
定义:输入和输出能唯一确定初始状态 x ( t 0 ) x(t_0) x(t0)
二、可观测性的一般判别准则
①状态方程在 [ t 0 , t 1 ] [t_0,t_1] [t0,t1]可控的充要条件: C ( t ) Φ ( t , t 0 ) C(t)\Phi(t,t_{0}) C(t)Φ(t,t0)的n个列在时间内线性无关
②
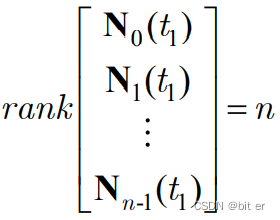
其中: N k ( t ) = N k − 1 ( t ) A ( t ) + d N k − 1 ( t ) d t N_{k}(t)=N_{k-1}(t)A(t)+\frac{\mathrm{d} N_{k-1}(t)}{\mathrm{d} t} Nk(t)=Nk−1(t)A(t)+dtdNk−1(t)、 N 0 ( t ) = C ( t ) N_0(t)=C(t) N0(t)=C(t)
③n维方程在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)对每一个t均微分可观的充要条件是:
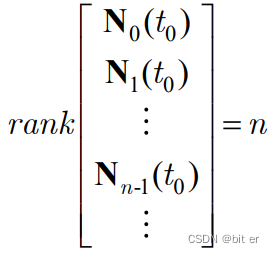
三、可重构性
可重构性是通过过去信息判断现在状态,而可观测性是用未来的信息判别现在的状态
判别方法:
C ( τ ) Φ ( τ , t 0 ) C(\tau)\Phi(\tau,t_{0}) C(τ)Φ(τ,t0)列线性无关,即 ∫ t 1 t 2 Φ ∗ ( τ , t 0 ) C ∗ ( τ ) C ( τ ) Φ ( τ , t 0 ) d t \int_{t_{1}}^{t_{2}} \Phi^*(\tau,t_{0}) C^*(\tau)C(\tau)\Phi(\tau,t_{0}) d t ∫t1t2Φ∗(τ,t0)C∗(τ)C(τ)Φ(τ,t0)dt非奇异
四、线性系统的对偶性
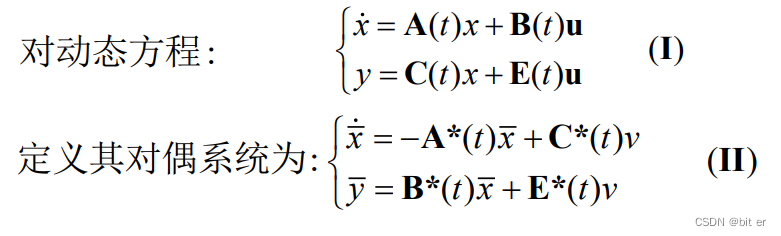
( I ) (I) (I)在 t 0 t_0 t0可控(可达) ⟺ \Longleftrightarrow ⟺ ( I I ) (II) (II)在 t 0 t_0 t0k可观测(可重构)
( I ) (I) (I)在 t 0 t_0 t0可观测(可重构) ⟺ \Longleftrightarrow ⟺ ( I I ) (II) (II)在 t 0 t_0 t0k可控(可达)
五、线性时不变系统的可观测性判据
常用:PBH判据、秩判据、Gram非奇异、列线性无关
5.5 线性时不变系统的规范分解
一、等价变换的性质
在任何等价变换之下,线性时不变系统的可控和可观不变
二、动态方程按可控性分解
1、定义
可控分解变换完之后的标准形:
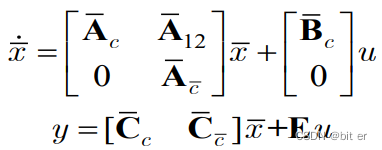
其中可控部分的动态方程和原系统有相同的传递函数阵(不反应不可控部分)
2、步骤
①列可控性矩阵: U = r a n k [ B A B . . . A n − 1 B ] = n 1 U=rank[B\quad AB ... \quad A^{n-1}B]=n_1 U=rank[BAB...An−1B]=n1
②取 n 1 n_1 n1个线性无关的列向量,之后补充上 n − n 1 n-n_1 n−n1个线性无关的列向量,构成 P − 1 P^{-1} P−1
③做变换: A ‾ = P A P − 1 \overline{\mathbf{A}}=\mathbf{P A} \mathbf{P}^{-1} A=PAP−1、 B ‾ = P B \overline{\mathbf{B}}=\mathbf{P B} B=PB、 C ‾ = C P − 1 \overline{\mathbf{C}}=\mathbf{C P}^{-1} C=CP−1、 E ˉ = E \bar{E}=E Eˉ=E
三、动态方程的可观性分解
1、定义
可观分解变换完之后的标准形:
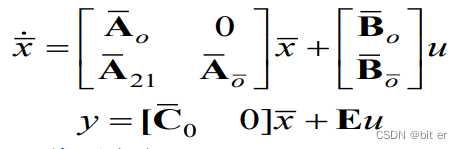
其中可观部分的动态方程和原系统有相同的传递函数阵(不反应不可观测部分)
2、步骤
①列可控性矩阵: U = r a n k [ C C A . . . C A n − 1 ] T = n 2 U=rank[C\quad CA ... \quad CA^{n-1}]^T=n_2 U=rank[CCA...CAn−1]T=n2
②取 n 2 n_2 n2个线性无关的行向量,之后补充上 n − n 2 n-n_2 n−n2个线性无关的列向量,构成 P P P
③做变换: A ‾ = P A P − 1 \overline{\mathbf{A}}=\mathbf{P A} \mathbf{P}^{-1} A=PAP−1、 B ‾ = P B \overline{\mathbf{B}}=\mathbf{P B} B=PB、 C ‾ = C P − 1 \overline{\mathbf{C}}=\mathbf{C P}^{-1} C=CP−1、 E ˉ = E \bar{E}=E Eˉ=E
四、规范分解定理
通过观察 B和C矩阵 来判断状态变量中的 可控和可观状态
注意:
这些不出现在传递函数矩阵中的部分其状态行为不可避免地要影响系统的稳定性和品质,这是我们在系统设计中要特别注意的。
五、不可简约的动态方程
1、定义
如果不存在相同传递函数阵,但是维数更低的系统,则不可简约
2、
不可简约 的充要条件是 动态方程是可控可观测的
如果同一个传递函数阵,存在两个不同的动态方程实现,则存在变换关系 P P P矩阵
5.6 约当形(若当)动态方程的可控性和可观测性
名词解释:

**可控性判据:**行线性无关
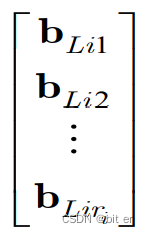
**可观性判据:**列线性无关
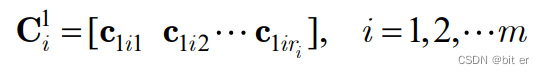
注意:只有一个块的时候,只需要不全为0即可
5.7 输出可控性
1、定义
存在能将输出 y ( t 0 ) = 0 y(t_0)=0 y(t0)=0转移到 y ( t 1 ) = y 1 y(t_1)=y_1 y(t1)=y1的输入 u [ t 0 , t 1 ] u[t_0,t_1] u[t0,t1],则称系统在 t 0 t_0 t0是输出可控
2、判据
时变:连续脉冲响应矩阵 G ( t , τ ) G(t,\tau) G(t,τ)的所有行线性无关
时不变: [ C B C A B . . . C A n − 1 B ] [CB\quad CAB\quad ...\quad CA^{n-1}B] [CBCAB...CAn−1B]满秩
5.8.4 连续系统时间离散化后保持可控和可观测条件
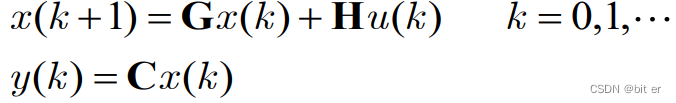
G = e A T G=e^{AT} G=eAT、 H = ∫ 0 T e A T d t B H=\int_{0}^{T} e^{AT}dt \quad B H=∫0TeATdtB
时间离散化系统保持可控和可观测的充分条件是:
采样周期数值,对一切满足 R e [ λ i − λ j ] = 0 Re[\lambda_i-\lambda_j]=0 Re[λi−λj]=0的特征值,成立 T ≠ 2 l π Im ( λ i − λ j ) \mathrm{T} \neq \frac{2 l \pi}{\operatorname{Im}\left(\lambda_{\mathrm{i}}-\lambda_{\mathrm{j}}\right)} T=Im(λi−λj)2lπ
六、不可简约实现
6.1 引言
系统实现:具有指定有理传递函数矩阵 G ( s ) G(s) G(s)的线性时不变动态方程(无限多个)称为 G ( s ) G(s) G(s)的实现
标准形实现:套标准形实现的公式
最小实现:不可简约动态方程实现
6.2 正则有理矩阵的特征多项式和次数
动态方程实现是不可简约的条件: d e t ( s I − A ) = k det(sI-A)=k det(sI−A)=k(g(s)的分母)、 d i m ( A ) = d e g ( g ( s ) ) dim(A)=deg(g(s)) dim(A)=deg(g(s))
G ( s ) G(s) G(s)的次数:正则有理矩阵 G ( s ) G(s) G(s)的所有子式的最小公分母(特征多项式)的次数
6.3 正则有理函数的不可简约实现
一、单变量系统
1、可控标准形实现
传递函数:
g ( s ) = y ( s ) u ( s ) = β 1 s n − 1 + β 2 s n − 2 + … … + β n − 1 s 1 + β n s n + a 1 s n − 1 + … … + a n − 1 s 1 + a n s g(s)=\frac{y(s)}{u(s)}=\frac{\beta_{1} s^{n-1}+\beta_{2} s^{n-2}+\ldots \ldots+\beta_{n-1} s^{1}+\beta_{n}}{s^{n}+\mathrm{a}_{1} s^{n-1}+\ldots \ldots+a_{n-1} s^{1}+a_{n} s} g(s)=u(s)y(s)=sn+a1sn−1+……+an−1s1+ansβ1sn−1+β2sn−2+……+βn−1s1+βn
x ˙ = [ 0 1 0 0 0 0 1 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 0 1 − a n − a n − 1 − a n − 2 ⋯ − a 1 ] x + [ 0 0 ⋮ 0 1 ] u y = [ β n β n − 1 ⋯ β 2 β 1 ] x + e u \begin{aligned} \dot{x} &=\left[\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & & 1 & & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & 1 \\ -a_{n} & -a_{n-1} & -a_{n-2} & \cdots & -a_{1} \end{array}\right] x+\left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{array}\right] u \\ y &=\left[\begin{array}{lllll} \beta_{n} & \beta_{n-1} & \cdots & \beta_{2} & \beta_{1} \end{array}\right] x+e u \end{aligned} x˙y= 00⋮0−an1⋮0−an−101⋮0−an−20⋱0⋯00⋮1−a1 x+ 00⋮01 u=[βnβn−1⋯β2β1]x+eu
2、求可控标准形的步骤
①计算可控性矩阵 U = r a n k [ B A B . . . A n − 1 B ] U=rank[B\quad AB ... \quad A^{n-1}B] U=rank[BAB...An−1B]
②计算 U − 1 U^{-1} U−1,并取最后一行为h
③求变换阵 P = [ h h A h A 2 ⋮ h A n − 1 ] n × n \mathbf{P}=\left[\begin{array}{c} \mathbf{h} \\ \mathbf{h} \mathbf{A} \\ \mathbf{h} \mathbf{A}^{2} \\ \vdots \\ \mathbf{h} \mathbf{A}^{n-1} \end{array}\right]_{n \times n} P= hhAhA2⋮hAn−1 n×n
④ A ‾ = P A P − 1 \overline{\mathbf{A}}=\mathbf{P A} \mathbf{P}^{-1} A=PAP−1、 B ‾ = P B \overline{\mathbf{B}}=\mathbf{P B} B=PB、 C ‾ = C P − 1 \overline{\mathbf{C}}=\mathbf{C P}^{-1} C=CP−1
3、可观标准形实现

4、求可观标准型的步骤
①求可观矩阵判断可观,如果可观,则可以化为可观标准形
②写原系统的对偶系统 ( A → A T ) 、 ( b → c T ) 、 ( c → b T ) (A→A^T)、(b→c^T)、(c→b^T) (A→AT)、(b→cT)、(c→bT)
③做可控标准形转换 A ‾ 1 = P A T P − 1 \overline{\mathbf{A}}_1=\mathbf{P A^T} \mathbf{P}^{-1} A1=PATP−1、 b ‾ 1 = P c T \overline{\mathbf{b}}_1=\mathbf{P c^T} b1=PcT、 c ‾ 1 = b T P − 1 \overline{\mathbf{c}}_1=\mathbf{b^T P}^{-1} c1=bTP−1
二、多变量系统的标准形
1、Luenberger可控标准形

2、变换的步骤
①假设B列满秩,列出可控性矩阵 U = r a n k [ B A B . . . A n − 1 B ] U=rank[B\quad AB ... \quad A^{n-1}B] U=rank[BAB...An−1B]
②自左向右挑选n个线性无关的向量
③构造 P − 1 = [ b 1 A b 1 ⋯ A μ 1 − 1 b 1 b 2 A b 2 ⋯ A μ 2 − 1 b 2 ⋯ b p A b p ⋯ A μ p − 1 b p ] P^{-1}=\left[\mathbf{b}_{1} \quad\mathbf{A} \mathbf{b}_{1} \quad\cdots \mathbf{A}^{\mu_{1}-1} \mathbf{b}_{1} \quad\mathbf{b}_{2} \quad\mathbf{A} \mathbf{b}_{2} \cdots \mathbf{A}^{\mu_{2}-1} \mathbf{b}_{2} \cdots \mathbf{b}_{p} \quad\mathbf{A} \mathbf{b}_{p} \cdots \mathbf{A}^{\mu_{p}-1} \mathbf{b}_{p}\right] P−1=[b1Ab1⋯Aμ1−1b1b2Ab2⋯Aμ2−1b2⋯bpAbp⋯Aμp−1bp]
④求出 P 1 P_1 P1,以 h 1 h_1 h1表示 P 1 P_1 P1的第$\mu_1 $行
⑤构造变换阵 P 2 = [ h 1 h 1 A ⋮ h 1 A μ 1 − 1 h 2 ⋮ h 2 A μ 2 − 1 ⋮ h p ⋮ h p A μ P − 1 ] P_2=\left[\begin{array}{c} h_{1} \\ h_{1} A \\ \vdots \\ h_{1} A^{\mu_{1}-1} \\ h_{2} \\ \vdots \\ h_{2} \boldsymbol{A}^{\mu_{2}-1} \\ \vdots \\ \boldsymbol{h}_{p} \\ \vdots \\ h_{p} \boldsymbol{A}^{\mu_{P}-1} \end{array}\right] P2= h1h1A⋮h1Aμ1−1h2⋮h2Aμ2−1⋮hp⋮hpAμP−1
⑥做一系列的变换 A ‾ = P 2 A P 2 − 1 \overline{\mathbf{A}}=\mathbf{P_2 A} \mathbf{P}_2^{-1} A=P2AP2−1、 B ‾ = P 2 B \overline{\mathbf{B}}=\mathbf{P_2 B} B=P2B、 C ‾ = C P 2 − 1 \overline{\mathbf{C}}=\mathbf{C P}_2^{-1} C=CP2−1
三、正则有理传递函数的最小实现
1、可控标准形的最小阶实现
2、可观测标准形的最小阶实现
3、由汉克尔矩阵实现步骤
①观察传递函数 g ( s ) = y ( s ) u ( s ) = β 0 s n + β 1 s n − 1 + β 2 s n − 2 + … … + β n − 1 s 1 + β n s n + a 1 s n − 1 + … … + a n − 1 s 1 + a n s g(s)=\frac{y(s)}{u(s)}=\frac{\beta_0 s^n+\beta_{1} s^{n-1}+\beta_{2} s^{n-2}+\ldots \ldots+\beta_{n-1} s^{1}+\beta_{n}}{s^{n}+\mathrm{a}_{1} s^{n-1}+\ldots \ldots+a_{n-1} s^{1}+a_{n} s} g(s)=u(s)y(s)=sn+a1sn−1+……+an−1s1+ansβ0sn+β1sn−1+β2sn−2+……+βn−1s1+βn
②套公式:利用迭代法进行多项式的除法来求系数,见例题
③套矩阵:
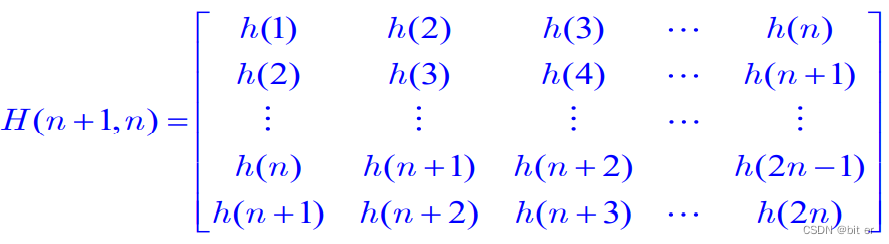
④利用 α H ( n + 1 , n ) = 0 \alpha H(n+1,n)=0 αH(n+1,n)=0来确定标准形的最后一层系数 α \alpha α
4、若当标准形实现
见例题
6.4 多变量系统的实现
一、动态方程的可控性、可观性与传递函数阵之间的关系
如果 G ( s ) G(s) G(s)的分子和分母之间没有非常数的公因式,则系统是可控和可观的
系统可观和可控的充要条件是 G(s)的极点多项式等于A的特征多项式
二、向量传递函数的实现
1、行分母展开得可观标准形
2、列分母展开的可控标准形
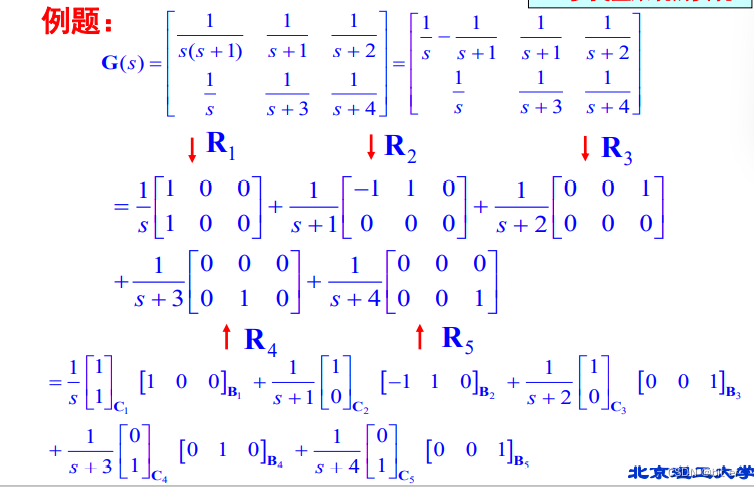
三、传递函数矩阵G(s)的实现
1、列展开步骤:(可控标准型实现)

2、行展开步骤:(可观测标准型实现)

注意:
1、其中B矩阵的的N是从常数项开始写的
2、之后如果不可控,需要进行可控分解的变换,之后必须留下可控可观的部分
3、约当形展开
七、状态反馈和状态观测器
7.2 状态反馈
一、状态反馈对可控可观的影响
状态反馈不改变系统的可控性,但是可能改变系统的可观性
二、输出反馈对可控可观的影响
对于连续线性时不变系统,输出反馈可以保持系统的可控性和可观性
三、单输入系统的极点配置
条件:系统需要改变的模态可控
计算步骤:
①计算 d e t ( s I − ( A + b K ) ) det(sI-(A+bK)) det(sI−(A+bK))
②计算所给特征值的期望多项式
③相等来求解方程
方框图:
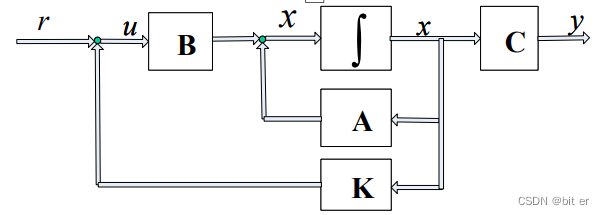
四、状态反馈对传递函数零点的影响
状态反馈可移动极点,一般不影响零点,但可能存在零极点对消情况(影响零极点)
七、镇定问题
判定条件:系统的特征值均具有负实部(可控系统或者不可控系统的不可控模态具有负实部)
7.3 状态观测器
二、状态观测器的存在性、n为状态观测器
条件:系统可观测
三、单输入单输出系统的状态观测器
①计算 d e t ( s I − A ) det(sI-A) det(sI−A)和期望特征多项式
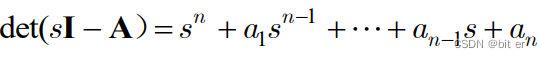
②构造P矩阵 [ a n − 1 a n − 2 ⋯ a 1 1 a n − 2 1 ⋮ ⋮ a 1 1 0 1 ] [ c c A ⋮ c A n − 1 ] \left[\begin{array}{ccccc} a_{n-1} & a_{n-2} & \cdots & a_{1} & 1 \\ a_{n-2} & & & 1 & \\ \vdots & & \vdots & & \\ a_{1} & 1 & & 0 & \\ 1 & & & & \end{array}\right]\left[\begin{array}{c} \mathbf{c} \\ \mathbf{c A} \\ \vdots \\ \mathbf{c A}^{n-1} \end{array}\right] an−1an−2⋮a11an−21⋯⋮a1101 ccA⋮cAn−1
③列 l ˉ = [ a ˉ n − a n a ˉ n − 1 − a n − 1 ⋮ ⋮ a ˉ 1 − a 1 ] \bar{l}=\left[\begin{array}{c} \bar{a}_{n}-a_{n} \\ \bar{a}_{n-1}-a_{n-1} \\ \vdots \\ \vdots \\ \bar{a}_{1}-a_{1} \end{array}\right] lˉ= aˉn−anaˉn−1−an−1⋮⋮aˉ1−a1 之后带入到 l = P − 1 l ˉ l=P^{-1}\bar l l=P−1lˉ
④求的 x ^ ˙ = ( A − l C ) x ^ + b u + l y \dot {\hat{x}}=(A-lC)\hat{x} +bu+ly x^˙=(A−lC)x^+bu+ly
方框图如下:
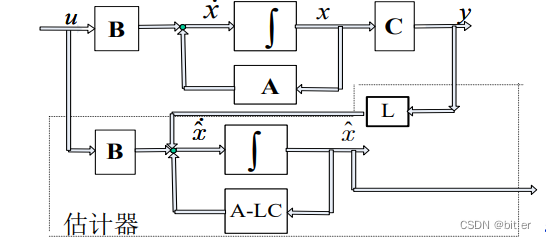
五、最小维状态观测器
7.4 状态反馈与状态观测器的连接
一、包括观测器的状态反馈系统的构成
条件:系统可控、可观
①估计器: x ^ ˙ = ( A − l C ) x ^ + b u + l y \dot {\hat{x}}=(A-lC)\hat{x} +bu+ly x^˙=(A−lC)x^+bu+ly
②状态反馈: u = r + K x ^ u=r+K \hat{x} u=r+Kx^
组合: x ^ ˙ = ( A − l C + b K ) x ^ + b r + l y \dot {\hat{x}}=(A-lC+bK )\hat{x} +br+ly x^˙=(A−lC+bK)x^+br+ly
二、包括观测器的状态反馈系统的特性
1、组合系统的维数:2n
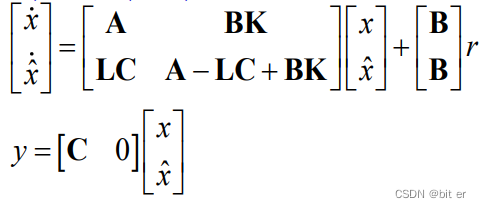
2、等价变换后的动态方程:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l8BLH6EI-1670243541448)(C:\Users\91996\AppData\Roaming\Typora\typora-user-images\image-20221202214303542.png)]](https://img-blog.csdnimg.cn/fb268dd1d33a40828175d774401d67d7.png)
可以看出来估计器不影响系统的传递函数
3、分离性原理
分离性原理:若系统(A, B,C)可控、可观,对于包含估计器的状态反馈系统,状态反馈律的设计和估计器的设计可独立地分开进行
八、线性系统的稳定性
8.1 李氏稳定
稳定条件: d e t ( s I − A ) = 0 det(sI-A)=0 det(sI−A)=0的特征根都在负实部
特殊:
其中当具有 s = 0 s=0 s=0的重根时候,看代数重复度(次数)=几何重复度( n − r a n k ( λ i I − A ) n-rank(\lambda_iI-A) n−rank(λiI−A))时候稳定
充要条件:
李氏稳定: d e t ( s I − A ) det(sI-A) det(sI−A)实部为零的根对应的初等因子是一次(或者几何重数等于代数重数),且其余根均具有负实部
渐近稳定: d e t ( s I − A ) det(sI-A) det(sI−A)的所有根均具有负实部
8.2 线性时不变系统的稳定性分析
可控分解标准型:
x ˉ ˙ = [ A ‾ c A ‾ 12 0 A ‾ c ˉ ] x ˉ + [ B ‾ c 0 ] u y = [ C ‾ c C ‾ c ˉ ] x ˉ + E u \begin{array}{c} \dot{\bar{x}}=\left[\begin{array}{cc} \overline{\mathbf{A}}_{c} & \overline{\mathbf{A}}_{12} \\ 0 & \overline{\mathbf{A}}_{\bar{c}} \end{array}\right] \bar{x}+\left[\begin{array}{c} \overline{\mathbf{B}}_{c} \\ 0 \end{array}\right] u \\ y=\left[\overline{\mathbf{C}}_{c} \quad \overline{\mathbf{C}}_{\bar{c}}\right] \bar{x}+\mathbf{E} u \end{array} xˉ˙=[Ac0A12Acˉ]xˉ+[Bc0]uy=[CcCcˉ]xˉ+Eu
可观分解标准型:
x ‾ ˙ = [ A ‾ o 0 A ‾ 21 A ‾ o ˉ ] x ‾ + [ B ‾ o B ‾ o ˉ ] u y = [ C ‾ 0 0 ] x ˉ + E u \begin{array}{c} \dot{\overline{\boldsymbol{x}}}=\left[\begin{array}{cc} \overline{\mathbf{A}}_{o} & \mathbf{0} \\ \overline{\mathbf{A}}_{21} & \overline{\mathbf{A}}_{\bar{o}} \end{array}\right] \overline{\boldsymbol{x}}+\left[\begin{array}{l} \overline{\mathbf{B}}_{o} \\ \overline{\mathbf{B}}_{\bar{o}} \end{array}\right] u \\ y=\left[\begin{array}{ll} \overline{\mathbf{C}}_{0} & 0 \end{array}\right] \bar{x}+\mathbf{E} u \end{array} x˙=[AoA210Aoˉ]x+[BoBoˉ]uy=[C00]xˉ+Eu
状态、输出公式:
x ( t ) = Φ ( t , t 0 ) x 0 + ∫ t 0 t Φ ( t , τ ) B ( τ ) u ( τ ) d τ x(t)=\Phi(t,t_0)x_0+\int_{t_0}^{t} \Phi(t,\tau)B(\tau)u(\tau)d\tau x(t)=Φ(t,t0)x0+∫t0tΦ(t,τ)B(τ)u(τ)dτ
y ( t ) = C ( t ) Φ ( t , t 0 ) x 0 + ∫ t 0 t C ( t ) Φ ( t , τ ) B ( τ ) u ( τ ) d τ y(t)=C(t)\Phi(t,t_0)x_0+\int_{t_0}^{t} C(t)\Phi(t,\tau)B(\tau)u(\tau)d\tau y(t)=C(t)Φ(t,t0)x0+∫t0tC(t)Φ(t,τ)B(τ)u(τ)dτ
判别条件:
BIBS稳定( x ( t 0 ) = 0 x(t_0)=0 x(t0)=0) ⟺ \Longleftrightarrow ⟺可控部分收敛
BIBS全稳定( x ( t 0 ) x(t_0) x(t0)任意) ⟺ \Longleftrightarrow ⟺可控部分收敛,不可控部分不发散
BIBO稳定( x ( t 0 ) = 0 x(t_0)=0 x(t0)=0) ⟺ \Longleftrightarrow ⟺可控可观部分收敛
BIBO全稳定( x ( t 0 ) x(t_0) x(t0)任意) ⟺ \Longleftrightarrow ⟺可控可观部分收敛,可观不可控部分不发散
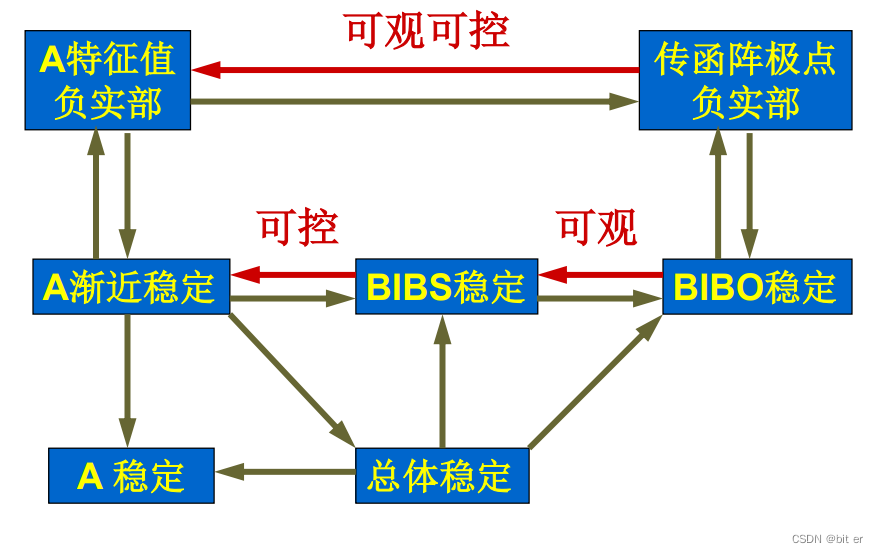
三、总体稳定(T稳定)
T稳定=BIBS全稳定
关系图
![[外链图片转存中...(img-eOEyPDJa-1670243541448)]](https://img-blog.csdnimg.cn/555f8e13f68a4ea780bfe4da2c4fdb33.png)