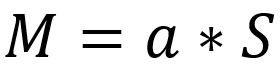目录
- 平衡二叉树
- AVLtree数据结构
- 插入
- 左旋
- 右旋
- 右左双旋
- 左右双旋
- 完整AVLTree插入代码如下
- AVLTree的验证
- AVLTree删除【了解】
- AVLTree性能分析
- 红黑树
- 红黑树性质
- RBTree数据结构
- 插入
- 情况一:cur为红,p为红,g为黑,u存在且为红
- 情况二:cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]
- cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]
- 完整的插入代码
- RBTree验证
- 多路查找树
- 2-3树
- 2-3-4树
- B树
- BTree数据结构
- BTree实现
- BTree性能分析
- B-树删除
- B+树
- B*树
- 简短的总结
- B树应用
- 索引
- MySQL的索引
- MyISAM
- Innodb
- 图
- 概念
- 数据结构
- 邻接矩阵
- 邻接表
- 图的遍历
- 广度优先遍历
- 深度优先遍历
- 最小生成树
- Kruskal算法
- Prime算法
- 最短路径
- 单源最短——Dijkstra
- 单源最短——Bellman-Ford
- 多源最短——Floyd-Warshall
好久没有更新博客了,拖了这么久,这次带来绝对的干货,顺带一提的是,替换掉了之前用PPT画图的方案,终于找到了一款合适的画图软件——draw.io
起初是在网页上找到的这个流程图,后来想下载下来本地使用,所以就搜索了一下,发现这是GitHub上的一个开源软件,索性就下载是用了一番,感觉效果不错,上手简单,而且画图质量比之前的PPT高了不止一个档次
离线网站;GitHub离线下载到本地
processon
平衡二叉树
二叉搜索树的增删改查都需要依据查找,因此差找的效率就决定了二叉树的性能天花板。
最优情况下,查找一棵完全二叉树则是log2n【n是树的高度】
最差情况下,二叉树退化成单分之树,此时查找效率和链表的差找效率类似,都是n
提升效率有两个手段:减少比较次数、减少交换次数
树形结构,我们常用的堆排序就是优化冒泡排序的,达到减少比较合交换来提升效率;而二叉树的提升,我们分析之后,发现涉及到的交换很少,只有比较和旋转操作,而旋转操作是AVLTree的核心;因此我们把重心放在减少比较次数上
而影响树的高度的就是树的形状,当我们把高度调低之后是不是变相的减少了树的高度,那么就可以减少比较次数了呢?因此AVLTree也就诞生了
AVLtree数据结构
public class AVLTree {static class TreeNode {public int val;public int bf;// 平衡因子public TreeNode left;// 左孩子引用public TreeNode parent;// 父节点引用public TreeNode right;// 右孩子引用public TreeNode(int val) {this.val = val;}}public TreeNode root;// 父节点
}
插入
左旋
插入过程类分为两部分,第一部分和平衡二叉树一模一样;第二部分则需要从插入节点的父节点开是更改平衡因子
如下图所示:当插入 node(10)节点
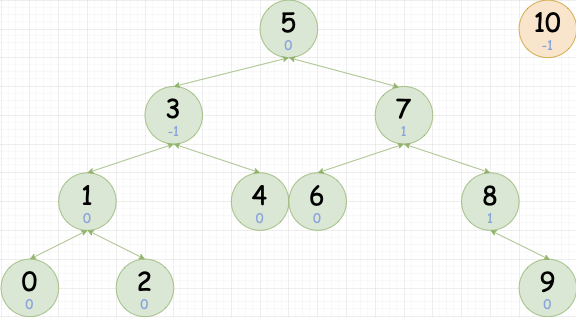
public boolean insert(int val) {TreeNode node = new TreeNode(val);if (root == null) {root = node;} else {TreeNode parent = null;TreeNode cur = root;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur == null,pre记录cur父节点if (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;
}
这段代码开头就是模仿平衡二叉树的思路,如果有不会的,可以查阅我的博客——当初我这么学习二叉树就好了
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9Di03IHY-1666368041421)(../resources/DataStructure/AVLtree/左旋前.png)]](https://img-blog.csdnimg.cn/1d90beba8d6b42ce8eba5b07ba17ca65.png)
此时发现 node(8) 节点不平衡,此时我们就需要通过 左旋 的方式来达到目的
public boolean insert(int val) {TreeNode node = new TreeNode(val);if (root == null) {root = node;} else {TreeNode parent = null;TreeNode cur = root;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur == null,pre记录cur父节点if (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;// 更新平衡因子cur = node;while (cur != null) {// 1.先看 cur 是 parent 的左还是右决定平衡因子++还是--if (cur == parent.left) {// 如果是左树,平衡因子----parent.bf;} else {// 如果是右树,平衡因子++++parent.bf;}// 2.检查平衡因子是不是绝对值 1 0 -1if (parent.bf == 0) {// 已经平衡break;} else if (parent.bf == 1 || parent.bf == -1) {// 继续向上调节平衡因子cur = parent;parent = cur.parent;} else {if (parent.bf == 2) {// 右树高if (cur.bf == 1) {// 左旋} else {// cur.bf == -1 右左双旋}} else {// 左树高if (cur.bf == 1) {// 右旋} else {// cur.bf == -1,左树高,左右双旋}}}}}
}
并不是所有右树高的情况都适合左旋,我们在这里先记下此时的情况
如下图所示:当出现 parent 和 cur 都是同号且为正数,就可以左旋;如果都为负数,则需要右旋
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Hj24Eq0z-1666368041421)(../resources/DataStructure/AVLtree/左旋后.png)]](https://img-blog.csdnimg.cn/94fbd10f071047328581b7a4cc9ab5bc.png)
为何称为左旋?
我们发现,这种方案就相当于把 node(8) 给移动到了左边来降低右树的高度,所以就称之为 左旋
插入成功之后我们还需要更改平衡因子【注意红色的数字变化就是修改平衡因子】,话不多说,上代码。
private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;subR.left = parent;parent.right = subRL;if (subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if (parent == root) {root = subR;root.parent = null;} else {if (pParent.left == parent) {pParent.left = subR;} else {pParent.right = subR;}subR.parent = pParent;}
}
其实本质代码是这四个然后加上简单的非空判断和是否跟节点的判断
subR.left = parent;
parent.right = subRL;
subRL.parent = parent;// 需要做非空判断
爷爷节点.left/right = subR;// 在此之前提前保留爷爷节点
subR.parent = 爷爷节点;// 连接
到这里之后最后完成修改bf平衡因子值为0即可
private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;subR.left = parent;parent.right = subRL;if (subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if (parent == root) {root = subR;root.parent = null;} else {if (pParent.left == parent) {pParent.left = subR;} else {pParent.right = subR;}subR.parent = pParent;}subR.bf = parent.bf = 0;
}
右旋
理解了左旋的以及为何称之为左旋,右旋也就很容易理解
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wEB2LQbt-1666368041422)(../resources/DataStructure/AVLtree/右旋插入前.png)]](https://img-blog.csdnimg.cn/622bf86d08414f4da37c842b41a76da2.png)
按着平衡二叉树的套路,新插入的 node(-1) 会落在 node(0).left
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yAKZ88pu-1666368041422)(../resources/DataStructure/AVLtree/右旋前.png)]](https://img-blog.csdnimg.cn/f121e49c632d4bcaab7016940d3af1ca.png)
此时发现 node(3) 节点不平衡,此时我们就需要通过 右旋 的方式来达到目的
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uPiU1Nfx-1666368041423)(../resources/DataStructure/AVLtree/右旋后.png)]](https://img-blog.csdnimg.cn/0616426e8287466eafdcb725fbe4a7c7.png)
右旋代码如下,这里就不一一剖析了【详情都在左旋,不重复啰嗦】
private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;subL.right = parent;parent.left = subLR;if (subLR != null) {subLR.parent = parent;subLR.bf = 0;}TreeNode pParent = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (pParent.left == parent) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}subL.bf = parent.bf = 0;
}
右左双旋
如果以上两个例子理解之后就可以进行双旋部分的阅读【代码很少,理解为主】
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LiNylHDB-1666368041425)(../resources/DataStructure/AVLtree/右左双旋插入前.png)]](https://img-blog.csdnimg.cn/c5b2c6b2a0714146a0085519166d7ab9.png)
插入后下如下图所示
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GxK9hlfu-1666368041426)(../resources/DataStructure/AVLtree/右左双旋插入后.png)]](https://img-blog.csdnimg.cn/f099e7d91ef74ed3bfc2f3c16cd39eb1.png)
此时发现明显是右树高,我们位了降低右树高度,那么 可以继续摸石头过河采取左旋吗?
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HNYlMG7O-1666368041427)(../resources/DataStructure/AVLtree/右左双旋_左旋替代演示.png)]](https://img-blog.csdnimg.cn/f8de61572ba44411a55b60ad0698a69c.png)
发现还是回到了老路—— node(8)的bf的确降低了,但是引来了node(10)的bf增加 相当于旋转了个寂寞
思考:每次我们都可以通过对应节点的旋转来达到降低本身高度的本质就是调整子节点的左右子树subR/RL和父节点parent本身的位置
右树高:左旋,交换了parent和subLR/subRL的位置,使其都变为提升上去节点的子节点,这样可以削减一层树的高度
但是这次的左旋并未达到理想效果,因此我们思考:既然parent以上和同级节点【上图中的node(8)以上的父节点和兄弟借点】都是平衡的,那么我们不能修改他们
问题来了:该旋转父节点本身还是子节点?答案显而易见的是:修改子subR/subRL节点
经过以上分析之后,所以我们把重点放在子节点上
那么8,9,10节点如何保持着搜索二叉树的结构摆放呢?很简单,也只能如下摆放
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RRBnACir-1666368041428)(../resources/DataStructure/AVLtree/右左双旋理想状态.png)]](https://img-blog.csdnimg.cn/b498f6eb6f534f5d8502fb0ff300f3df.png)
要想把某个节点提上去当作父节点,必须通过旋转,之后该节点的父节点成为了该节点的子节点,而子节点跃升为父节点方式才可以【有种我喊你哥哥,你喊我爸爸的意思】
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HrOrDWGE-1666368041428)(../resources/DataStructure/AVLtree/被提升节点.png)]](https://img-blog.csdnimg.cn/0f44136cd7f745ae8718eee664e2f9e3.png)
对此我们研究如何提升 node(9) 节点。要像夺取 node(8) 节点的位置,不能操之过急,只能步步为营才行。因此我们重点在放到node(10) 上。
node(9) 如何夺取 node(10) 位置呢
对于 node(10) 而言,左树高,通过 右旋 之后 node(9) 就会夺取 node(10) 位置,此时朋友可能会问:那之后不就是 node(10) 右树高了吗?
先别急,先让它高高在上一会儿,我们继续下一步操作就会柳暗花明起来
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2YrZ0xxz-1666368041429)(../resources/DataStructure/AVLtree/右左双旋右.png)]](https://img-blog.csdnimg.cn/20bb8bb408f941f5a104e70158788b24.png)
由于利用得上之前右旋的函数,所以就会修改 node(8) ,node(10) 节点的平衡因子bf值被修改为0
rotateRight(node(10));
此时发现还是右树高,我们这个时候再开是左旋【会有奇迹发生】
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Pd2ohHKk-1666368041430)(../resources/DataStructure/AVLtree/右左双旋右左.png)]](https://img-blog.csdnimg.cn/0adb6828a1f54848a5d9b1f31aebb034.png)
这样就可以达到平衡的高度差不超过1了
rotateLeftnode((8))
这里也少考虑了一个节点,当前代码和示意图是没问题的,当如果多出了那一个节点的话就会出现一定的BUG,详情可以查看左右双旋
如下图完整所示
当插入在最高节点的左右两侧,会出现不同的bf值效果:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tHUAk9JV-1666368041431)(../resources/DataStructure/AVLtree/右左双旋右_右左1.png)]](https://img-blog.csdnimg.cn/c19297dbe7e04d08b536b95319b1fbec.png)
左右双旋
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iQgO9Yuh-1666368041432)(../resources/DataStructure/AVLtree/左右双旋未左右.png)]](https://img-blog.csdnimg.cn/4378b002d27e48e0b7654375f90b102e.png)
此时左树高,如果单纯的右旋降低左树高度呢?
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NJmRVhDP-1666368041432)(../resources/DataStructure/AVLtree/左右双旋_右旋替代演示.png)]](https://img-blog.csdnimg.cn/391e18b361b44f72b3dad7e651f00dd6.png)
发现还是不可以。这里解释一下图片中数字的含义【图3⃣️】
node(0) 代表的是0节点
0:之前的状态为0,是平衡态【图1⃣️】
1:现在右旋之后右树高,此是的1应该是正确的bf值【图3⃣️】【理应正确的bf值】
【0】:经过之前rotateRight(node(3))旋转之后,parent.bf = subL.bf = 0,双旋状态下不一定是正确的【被程序修改的bf值,不一定代表正确】
因此我门参考之前右左双选的思想,继续把重点放在 node(0)【图2⃣️】,然后先左旋rotateLeft(node(0)),在右旋(rotateRight(node(3)))
插入在较高左子树的右侧
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fYYyhI1o-1666368041433)(../resources/DataStructure/AVLtree/左右双旋左右_1.png)]](https://img-blog.csdnimg.cn/20c65dc7d47b4b509cc812145fd64af1.png)
插入在较高左子树的左侧
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-apY4Bd4p-1666368041433)(../resources/DataStructure/AVLtree/左右双旋左右_2.png)]](https://img-blog.csdnimg.cn/e52b15237a6b42e19f46bc68fe45cea6.png)
途中我标注的都是前一幅图的旋转标记
插入node(2) 标注的是 rotateLeft(node(0)) 图中旋转之前的点,因为关于 parent和sub 节点的平衡因子需要修改,既然是人为修改,双旋的过程就有可能出错,所以我们应该小心谨慎一些
完整AVLTree插入代码如下
package avlTree;public class AVLTree {static class TreeNode {public int val;public int bf;// 平衡因子public TreeNode left;// 左孩子引用public TreeNode parent;// 父节点引用public TreeNode right;// 右孩子引用public TreeNode(int val) {this.val = val;}}public TreeNode root;// 父节点public boolean insert(int val) {TreeNode node = new TreeNode(val);if (root == null) {root = node;} else {TreeNode parent = null;TreeNode cur = root;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur == null,parent 记录 cur 父节点if (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;// 更新平衡因子cur = node;while (parent != null) {// 1.先看 cur 是 parent 的左还是右决定平衡因子++还是--if (cur == parent.left) {// 如果是左树,平衡因子----parent.bf;} else {// 如果是右树,平衡因子++++parent.bf;}// 2.检查平衡因子是不是绝对值 1 0 -1if (parent.bf == 0) {// 已经平衡break;} else if (parent.bf == 1 || parent.bf == -1) {// 继续向上调节平衡因子cur = parent;parent = cur.parent;} else {if (parent.bf == 2) {// 右树高if (cur.bf == 1) {// 左旋降低左树高度rotateLeft(parent);} else {// cur.bf == -1rotateRL(parent);}} else {// 左树高if (cur.bf == 1) {rotateLR(parent);} else {// cur.bf == -1rotateRight(parent);}}// 上述代码走早这里就平衡了,可以直接breakbreak;}}}return true;}private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if (bf == 1) {subR.bf = 0;subRL.bf = 0;parent.bf = -1;} else if (bf == -1) {subR.bf = 1;subRL.bf = 0;parent.bf = 0;}}private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;rotateLeft(parent.left);rotateRight(parent);if (bf == 1) {subL.bf = -1;subLR.bf = 0;parent.bf = 0;} else if (bf == -1) {subL.bf = 0;subLR.bf = 0;parent.bf = 1;}}private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;subR.left = parent;parent.right = subRL;if (subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if (parent == root) {root = subR;root.parent = null;} else {if (pParent.left == parent) {pParent.left = subR;} else {pParent.right = subR;}subR.parent = pParent;}subR.bf = parent.bf = 0;}private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;subL.right = parent;parent.left = subLR;if (subLR != null) {subLR.parent = parent;subLR.bf = 0;}TreeNode pParent = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (pParent.left == parent) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}subL.bf = parent.bf = 0;}
}
AVLTree的验证
有了AVLTree之后,我们还可以检查一棵树一下是否为AVLTree
AVLTree通过控制绝对的高度差来降低二叉搜索树的高度提高搜索效率,因此必须首先满足的是他是一个搜索二叉树其次是高度差不超过1
- 二叉树搜索树
- 高度平衡
对于如何验证一个树是一个二叉搜索树,这里有一个LeetCode题目110. 平衡二叉树可以先练一练【如果对搜索二叉树不熟悉的,阅读的我之前的博客——当初我要是这么学习二叉树就好了「附图文解析」】
// 中序遍历是有序的也不一定能说明AVL树
public void inorder(TreeNode root) {if (root == null) return;inorder(root.left);System.out.print(root.val + " ");inorder(root.right);
}private int height(TreeNode root) {if (root == null) return 0;int leftH = height(root.left);int rightH = height(root.right);return leftH > rightH ? leftH + 1 : rightH + 1;
}public boolean isAVLTree(TreeNode root) {if (root == null) return true;int leftH = height(root.left);int rightH = height(root.right);// 平衡因子如果出现旋转过程中更新出错,也不满足if (rightH - leftH != root.bf) {System.out.println(root.val + "平衡因子异常");return false;}return Math.abs(leftH - rightH) <= 1 && isAVLTree(root.left) && isAVLTree(root.right);
}
测试
public class Test {private static void AVLTreeTest() {
// int[] arr = {16, 3, 7, 11, 9, 26, 18, 14, 15};int[] arr = {4, 2, 6, 1, 3, 5, 15, 7, 16, 14};AVLTree avlTree = new AVLTree();for (int i = 0; i < arr.length; i++) {avlTree.insert(arr[i]);}boolean ret = avlTree.isAVLTree(avlTree.root);if (ret) {System.out.println("是AVLTree");} else {System.out.println("不是AVLTree");}System.out.print("中序遍历:");avlTree.inorder(avlTree.root);}public static void main(String[] args) {AVLTreeTest();}
}是AVLTree
中序遍历:1 2 3 4 5 6 7 14 15 16
可以放开注释的数组继续测试
AVLTree删除【了解】
- 找到要删除节点的替罪羊节点【左右子树的极值节点】
- 模仿二叉搜索树的删除
- 修改对应的平衡因子,如果出现不平衡则通过旋转的方式解决【单/双旋】
public void delete(TreeNode root, int val) {TreeNode pre = null;TreeNode cur = root;while (cur != null) {pre = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val){cur = cur.left;}else{// 找到了,就开始删除if (cur.right == null){// 1.只有左子树// 判断是否位根节点rootif(cur == root){root = root.left;}else if (cur == pre.left){pre.left = cur.left;}else if (cur == pre.right){pre.right = cur.left;}}else if (cur.left == null){// 2.只有右子树if (cur == root){root = root.right;}else if (cur == pre.left){pre.left = cur.right;}else if (cur == pre.right){pre.right = cur.right;}}else if (cur.left != null && cur.right != null){// 3.左右子树均有// 左子树找最大值【右子树找最小值】TreeNode targetParent = cur;// 这里选择左子树找最大值TreeNode target = cur.left;while (target.right != null){targetParent = target;target = target.right;}cur.val = target.val;if (target == targetParent.left){targetParent.left = target.right;}else{targetParent.right = target.right;}// 删除之后修改平衡因子,再通过单/双旋调整【代码目前好不会写】}}}
}
AVLTree性能分析
AVLTree是一棵绝对平衡的搜索二叉树,这样可以在查询的时候 log2n 内响应。但是涉及到插入、删除操作时,涉及到大量的旋转操作,更有甚者为了维持这个绝对的平衡誓不罢休要从叶子节点一路旋转到根节点才能保持住;也因此 AVLTree适合存储一些静态的数据,不用经常修改,近用来查询
红黑树
如果有些业务场景需要大量数据的增删改查,那么该如何解决呢?继续是用AVLTree的话由于大量的旋转导致性能太低下,因此聪明的科学家们准备削减AVLTree尊贵的面子——绝对平衡,退而求其次追求一种相对平衡状态,这样就在AVLTree的时间复杂度不变的情况下把行能低下的根源——大量旋转给削减。
红黑树:是一种接近平衡的二叉搜索树,通过 RED 或 BLACK 给每个节点增加一个颜色的存储位。通过任何一条路径上对 RED 或 BLACK 的颜色限制来确保没有任何一条路径的长度超过最短路径长度的2倍
红黑树性质
- 最长路径不超过最短路径2倍
- 每个节点非黑即红
- 跟节点为黑
- 一个红节点,两个孩子节点必须是黑【不能出现两个连续的红节点】
- 从根节点开始到叶子节点结束,每条路径上的黑节点个数相等
- 叶子节点是黑节点【此处的叶子节点就是空节点】
红黑树中如果有x个黑节点。
求黑树节点个数范围:假设全是黑节点,那么就是最少节点个数x;如果是红黑交替出现,则会是2x。所以答案是:[x,2x]的必区间
求时间复杂度: L o g 2 X Log_{2}{X} Log2X
- 最短: L o g 2 X Log_{2}{X} Log2X
- 最长: L o g 2 2 X = L o g 2 X + L o g 2 2 = L o g 2 2 X + 1 ≈ L o g 2 2 X Log_{2}{2X} = Log_{2}{X} + Log_{2}{2} = Log_{2}{2X}+1 \approx Log_{2}{2X} Log22X=Log2X+Log22=Log22X+1≈Log22X
RBTree数据结构
先创建一个颜色的枚举类COLOR
public enum ColorEnum {RED, BLACK;
}
public class RBTree {static class TreeNode{public TreeNode left;public TreeNode parent;public TreeNode right;public int val;public ColorEnum color;public TreeNode(int val) {this.val = val;// 默人新增节点是红色this.color=ColorEnum.RED;}}TreeNode root;
}
思考:为何新增点为红色而不是黑色
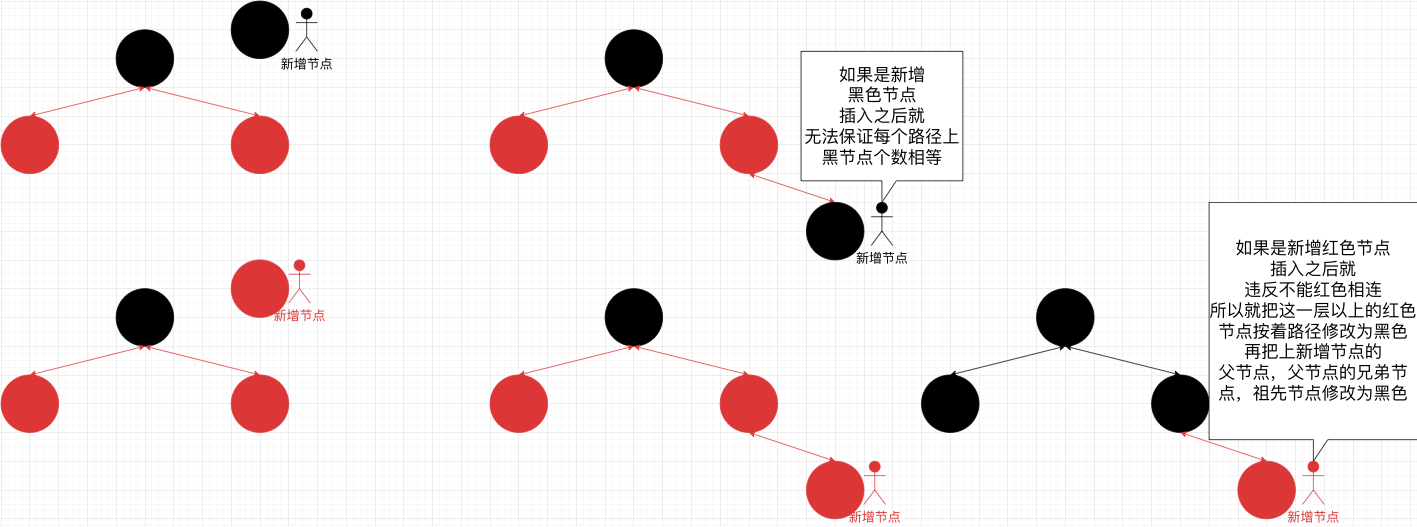
插入
插入的方式还是按照AVLTree的方式插入,因此可以直接复制之前修改平衡因子之前的代码
package rbtree;public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode parent;public RBTreeNode right;public int val;public ColorEnum color;public RBTreeNode(int val) {this.val = val;// 默人新增节点是红色this.color = ColorEnum.RED;}}public RBTreeNode root;public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;} else {RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur.parent = pre, cur=nullif (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 红黑树:调整颜色}}
}
后续判断是否满足红黑树性质我们需要先定义如下变量含义:
- cur:当前插入节点
- p:父节点
- u:父节点的兄弟借点
- g:父节点的父节点【祖先节点,爷爷节点】
情况一:cur为红,p为红,g为黑,u存在且为红
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lRAzK1qF-1666368560891)(../resources/DataStructure/RBTree/情况一.png)]](https://img-blog.csdnimg.cn/fe385f4ec0a74cfbacce5d8235cc1436.png)
这是最容易理解的图了,单是我们是不是忘记考虑 g节点 的父节点了呢?
看如下图所示
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mW56i7bk-1666368560900)(../resources/DataStructure/RBTree/情况一详解.png)]](https://img-blog.csdnimg.cn/6b170af17cfd41ff87a36ecc89351e76.png)
public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode parent;public RBTreeNode right;public int val;public ColorEnum color;public RBTreeNode(int val) {this.val = val;// 默人新增节点是红色this.color = ColorEnum.RED;}}RBTreeNode root;public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;root.color = ColorEnum.BLACK;} else {RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur.parent = pre, cur=nullif (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 红黑树:调整颜色while (parent != null && parent.color == ColorEnum.RED) {RBTreeNode grandFather = parent.parent;// 因为 p 是红节点,所以 g 一定不可能为空if (parent == grandFather.left){RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == ColorEnum.RED){// TODO 情况一:cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;}else{// TODO: 情况二:cur为红,p为红,g为黑,u不存在/u为黑}}else{// TODO}}}return true;}
}
上图中在调整过程出现连续了两个红色节点,这个时候该如何解决呢?
情况二:cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-55xsIxdZ-1666368560900)(../resources/DataStructure/RBTree/情况二.png)]](https://img-blog.csdnimg.cn/448c9b07bbac497c925edae47cdcfecf.png)
数一数高度,会发现最长路径为5;最短路径为2,明显已经违背红黑树定义
出现了高度问题,我们第一反应肯定是通过旋转来降低树的高度,最后观察是否满足红黑树性质再修改颜色
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HCv5h8UG-1666368560900)(../resources/DataStructure/RBTree/情况二详解.png)]](https://img-blog.csdnimg.cn/88a9ffafd6f9454c82f883bdfc1899cd.png)
public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode parent;public RBTreeNode right;public int val;public ColorEnum color;public RBTreeNode(int val) {this.val = val;// 默人新增节点是红色this.color = ColorEnum.RED;}}RBTreeNode root;public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;root.color = ColorEnum.BLACK;} else {RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur.parent = pre, cur=nullif (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 红黑树:调整颜色while (parent != null && parent.color == ColorEnum.RED) {RBTreeNode grandFather = parent.parent;// 因为 p 是红节点,所以 g 一定不可能为空if (parent == grandFather.left) {RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {// TODO 情况二: cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]rotateRight(grandFather);grandFather.color = ColorEnum.RED;parent.color = ColorEnum.BLACK;}} else {// TODO 情况三: cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]}}}return true;}private void rotateRight(RBTreeNode parent) {RBTreeNode subL = parent.left;RBTreeNode subLR = subL.right;subL.right = parent;parent.left = subLR;if (subLR != null) {subLR.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (parent == pParent.left) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}}
}
细心的小朋友发现我偷偷把cur放在p的left,而之前的例子是cur放在p的right
虽然和情况一不能整体贯通起来,但是我们可以先学一下这种方式【主要是为了更好的理解情况三】
cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8o4Q8Uj0-1666368560901)(../resources/DataStructure/RBTree/情况三.png)]](https://img-blog.csdnimg.cn/fec317d970c140baada699cb4fda1f48.png)
现在可以继续接着之前的讲解了,cur在p的右子树
还是发现最长路径为5,最短路径为2;需要通过旋转的方式达到效果
与情况二不同的是这次需要两次旋转:先左旋p;再右旋g
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qcgoe3j4-1666368560901)(../resources/DataStructure/RBTree/情况三详解.png)]](https://img-blog.csdnimg.cn/bf741edf235b4d45bcf985478751b57b.png)
public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode parent;public RBTreeNode right;public int val;public ColorEnum color;public RBTreeNode(int val) {this.val = val;// 默人新增节点是红色this.color = ColorEnum.RED;}}RBTreeNode root;public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;root.color = COLOR.BLACK;} else {RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur.parent = pre, cur=nullif (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 红黑树:调整颜色while (parent != null && parent.color == ColorEnum.RED) {RBTreeNode grandFather = parent.parent;// 因为 p 是红节点,所以 g 一定不可能为空if (parent == grandFather.left) {RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {// TODO 情况三: cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]if (cur == parent.right) {rotateLeft(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// 走到这里,就变成了情况二[情况三可以优先处理为情况二;如果没有情况三就直接执行情况二]// TODO 情况二: cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]rotateRight(grandFather);grandFather.color = ColorEnum.RED;parent.color = ColorEnum.BLACK;}} else {// TODO parent == grandFather.right}}}return true;}private void rotateLeft(RBTreeNode parent) {RBTreeNode subR = parent.right;RBTreeNode subRL = subR.left;subR.left = parent;parent.right = subRL;if (subRL != null) {subRL.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subR;if(parent == root){root = subR;root.parent = null;}else{if (parent == pParent.left) {pParent.left = subR;} else {pParent.right = subR;}subR.parent = pParent; }}private void rotateRight(RBTreeNode parent) {RBTreeNode subL = parent.left;RBTreeNode subLR = subL.right;subL.right = parent;parent.left = subLR;if (subLR != null) {subLR.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (parent == pParent.left) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}}
}
剩下的else语句如何呢?
还记得之前的if条件吗?如果 p==g.right 呢?我们继续向下分析。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-31CjhzCF-1666368560902)(../resources/DataStructure/RBTree/else_p右.png)]](https://img-blog.csdnimg.cn/28866d3dd55a44abbdf5677fb137e05a.png)
这一步和开始的一样: 修改颜色
代码复制if条件中的情况一的代码
package rbtree;public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode parent;public RBTreeNode right;public int val;public ColorEnum color;public RBTreeNode(int val) {this.val = val;// 默人新增节点是红色this.color = ColorEnum.RED;}}RBTreeNode root;public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;root.color = ColorEnum.BLACK;} else {RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur.parent = pre, cur=nullif (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 红黑树:调整颜色while (parent != null && parent.color == ColorEnum.RED) {RBTreeNode grandFather = parent.parent;// 因为 p 是红节点,所以 g 一定不可能为空if (parent == grandFather.left) {RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {// TODO 情况三: cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]if (cur == parent.right) {rotateLeft(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// 走到这里,就变成了情况二// TODO 情况二: cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]rotateRight(grandFather);grandFather.color = ColorEnum.RED;parent.color = ColorEnum.BLACK;}} else {// TODO parent == grandFather.rightRBTreeNode uncle = grandFather.left;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {}}}}return true;}private void rotateLeft(RBTreeNode parent) {RBTreeNode subR = parent.right;RBTreeNode subRL = subR.left;subR.left = parent;parent.right = subRL;if (subRL != null) {subRL.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subR;if(parent == root){root = subR;root.parent = null;}else{if (parent == pParent.left) {pParent.left = subR;} else {pParent.right = subR;}subR.parent = pParent;}}private void rotateRight(RBTreeNode parent) {RBTreeNode subL = parent.left;RBTreeNode subLR = subL.right;subL.right = parent;parent.left = subLR;if (subLR != null) {subLR.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (parent == pParent.left) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}}
}再复制情况二三代码,作出如下修改:
- 修改 if 的判断条件为 cur == parent.left
- 反向更改旋转操作即可
package rbtree;public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode parent;public RBTreeNode right;public int val;public ColorEnum color;public RBTreeNode(int val) {this.val = val;// 默人新增节点是红色this.color = ColorEnum.RED;}}RBTreeNode root;public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;root.color = ColorEnum.BLACK;} else {RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur.parent = pre, cur=nullif (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 红黑树:调整颜色while (parent != null && parent.color == ColorEnum.RED) {RBTreeNode grandFather = parent.parent;// 因为 p 是红节点,所以 g 一定不可能为空if (parent == grandFather.left) {RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {// TODO 情况三: cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]if (cur == parent.right) {rotateLeft(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// 走到这里,就变成了情况二// TODO 情况二: cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]rotateRight(grandFather);grandFather.color = ColorEnum.RED;parent.color = ColorEnum.BLACK;}} else {// TODO parent == grandFather.rightRBTreeNode uncle = grandFather.left;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {// 这段代码复制之前的情况二三: 然后修改 cur==parent.left;反向旋转 即可// TODO 情况三: cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]if (cur == parent.left) {rotateRight(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// 走到这里,就变成了情况二// TODO 情况二: cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]rotateLeft(grandFather);grandFather.color = ColorEnum.RED;parent.color = ColorEnum.BLACK;}}}}return true;}private void rotateLeft(RBTreeNode parent) {RBTreeNode subR = parent.right;RBTreeNode subRL = subR.left;subR.left = parent;parent.right = subRL;if (subRL != null) {subRL.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subR;if(root == parent){root = subR;root.parent = null;}else{if (parent == pParent.left) {pParent.left = subR;} else {pParent.right = subR;}subR.parent = pParent;}}private void rotateRight(RBTreeNode parent) {RBTreeNode subL = parent.left;RBTreeNode subLR = subL.right;subL.right = parent;parent.left = subLR;if (subLR != null) {subLR.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (parent == pParent.left) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}}
}
完整的插入代码
package rbTree;public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode parent;public RBTreeNode right;public int val;public ColorEnum color;public RBTreeNode(int val) {this.val = val;// 默人新增节点是红色this.color = ColorEnum.RED;}}public RBTreeNode root;public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;} else {RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else if (cur.val > val) {cur = cur.left;} else {return false;}}// cur.parent = pre, cur=nullif (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 红黑树:调整颜色while (parent != null && parent.color == ColorEnum.RED) {RBTreeNode grandFather = parent.parent;// 因为 p 是红节点,所以 g 一定不可能为空if (parent == grandFather.left) {RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {// TODO 情况三: cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]if (cur == parent.right) {rotateLeft(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// 走到这里,就变成了情况二// TODO 情况二: cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]rotateRight(grandFather);grandFather.color = ColorEnum.RED;parent.color = ColorEnum.BLACK;}} else {// TODO parent == grandFather.rightRBTreeNode uncle = grandFather.left;if (uncle != null && uncle.color == ColorEnum.RED) {// TODO 情况一: cur为红,p为红,g为黑,u存在且为红parent.color = ColorEnum.BLACK;uncle.color = ColorEnum.BLACK;grandFather.color = ColorEnum.RED;// 继续向上修改cur = grandFather;parent = cur.parent;} else {// 这段代码复制之前的情况二三: 然后修改 cur==parent.left;反向旋转 即可// TODO 情况三: cur为红,p为红,g为黑,u不存在/u为黑[p.right == cur]if (cur == parent.left) {rotateRight(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// 走到这里,就变成了情况二// TODO 情况二: cur为红,p为红,g为黑,u不存在/u为黑色[p.left == cur]rotateLeft(grandFather);grandFather.color = ColorEnum.RED;parent.color = ColorEnum.BLACK;}}}}root.color = ColorEnum.BLACK;return true;}private void rotateLeft(RBTreeNode parent) {RBTreeNode subR = parent.right;RBTreeNode subRL = subR.left;subR.left = parent;parent.right = subRL;if (subRL != null) {subRL.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subR;if (parent == root) {root = subR;root.parent = null;} else {if (parent == pParent.left) {pParent.left = subR;} else {pParent.right = subR;}subR.parent = pParent;}}private void rotateRight(RBTreeNode parent) {RBTreeNode subL = parent.left;RBTreeNode subLR = subL.right;subL.right = parent;parent.left = subLR;if (subLR != null) {subLR.parent = parent;}RBTreeNode pParent = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (parent == pParent.left) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}}public void inorder(RBTreeNode root) {if (root == null) return;inorder(root.left);System.out.print(root.val + " ");inorder(root.right);}public boolean isRBTree(RBTreeNode root) {if (root == null) return true;// 1.根节点必须为黑色if (root.color != ColorEnum.BLACK) {System.out.println(root.val + "违反性质: RBTree根节点必须为黑色");return false;}// 3.路径上黑色节点个数相等int blackNum = 0;RBTreeNode cur = root;while (cur != null) {if (cur.color == ColorEnum.BLACK) {++blackNum;}cur = cur.left;}// 2.检查是否存在两个连续的红色节点return checkRedColor(root) && checkBlackNum(root, 0, blackNum);}private boolean checkRedColor(RBTreeNode root) {if (root == null) return true;if (root.color == ColorEnum.RED) {RBTreeNode parent = root.parent;if (parent.color == ColorEnum.RED) {System.out.println(root.val + "违反性质: 不能出现两个连续的红节点");return false;}}return checkRedColor(root.left) && checkRedColor(root.right);}/*** @param root* @param pathBlackNum 递归到叶子节点时的黑节点个数* @param blackNum 是先计算好的黑节点个数* @return*/private boolean checkBlackNum(RBTreeNode root, int pathBlackNum, int blackNum) {if (root == null) return true;if (root.color == ColorEnum.BLACK) {++pathBlackNum;}if (root.left == null && root.right == null) {if (pathBlackNum != blackNum) {System.out.println(root.val + "违反性质: 黑色节点个数相等");}}return checkBlackNum(root.left, pathBlackNum, blackNum) && checkBlackNum(root.right, pathBlackNum, blackNum);}
}RBTree验证
AVLTree不能通过简单的中序遍历有序来判定,因为还需要额外的一个方法是判断高度差不超过1且等于该节点的平衡因子bf值。我们再根据RBTree的性质来判定即可。
- 首先是一棵二叉搜索树,因此可以通过简单的中序遍历来判定是否有序
- 根节点为黑
- 从任意节点出发,到叶子节点黑节点个数相等
- 不能出现连续的红节点
public void inorder(RBTreeNode root) {if (root == null) return;inorder(root.left);System.out.print(root.val + " ");inorder(root.right);
}public boolean isRBTree(RBTreeNode root) {if (root == null) return true;// 1.根节点必须为黑色if (root.color != COLOR.BLACK) {System.out.println(root.val + "违反性质: RBTree根节点必须为黑色");return false;}// 3.路径上黑色节点个数相等int blackNum = 0;RBTreeNode cur = root;while (cur != null) {if (cur.color == COLOR.BLACK) {++blackNum;}cur = cur.left;}// 2.检查是否存在两个连续的红色节点return checkRedColor(root) && checkBlackNum(root, 0, blackNum);
}private boolean checkRedColor(RBTreeNode root) {if (root == null) return true;if (root.color == COLOR.RED) {RBTreeNode parent = root.parent;if (parent.color == COLOR.RED) {System.out.println(root.val + "违反性质: 不能出现两个连续的红节点");return false;}}return checkRedColor(root.left) && checkRedColor(root.right);
}/*** @param root* @param pathBlackNum 递归到叶子节点时的黑节点个数* @param blackNum 是先计算好的黑节点个数* @return*/
private boolean checkBlackNum(RBTreeNode root, int pathBlackNum, int blackNum) {if (root == null) return true;if (root.color == COLOR.BLACK) {++pathBlackNum;}if (root.left == null && root.right == null) {if (pathBlackNum != blackNum) {System.out.println(root.val + "违反性质: 黑色节点个数相等");}}return checkBlackNum(root.left, pathBlackNum, blackNum) && checkBlackNum(root.right, pathBlackNum, blackNum);
}
最后就是测试环节
import rbTree.RBTree;public class Test {private static void RBTreeTest() {
// int[] arr = {16, 3, 7, 11, 9, 26, 18, 14, 15};int[] arr = {4, 2, 6, 1, 3, 5, 15, 7, 16, 14};RBTree rbTree = new RBTree();for (int i = 0; i < arr.length; i++) {rbTree.insert(arr[i]);}boolean ret = rbTree.isRBTree(rbTree.root);if (ret) {System.out.println("是RBTree");} else {System.out.println("不是RBTree");}System.out.print("中序遍历:");rbTree.inorder(rbTree.root);}public static void main(String[] args) {RBTreeTest();}
}是RBTree
中序遍历:1 2 3 4 5 6 7 14 15 16
多路查找树
电脑的文件管理其实就是一个树状图, 试想一下在一个拥有数十万个文件的磁盘中查找一个文本文件, 读取磁盘上万次还是读取几十次这是有本质上差异的. 而之前的树都是一个节点可以有多个孩子, 但它本身只存储一个元素. 二叉树限制更多, 节点最多只能有两个孩子.
一个节点只存储一个元素, 元素非常多的时候要么树的度非常大, 要么树的高度非常大, 甚至两者必须足够大才行.
多路查找树: 每一个节点的孩子数可以多于两个, 且每一个节点处可以存储多个元素.
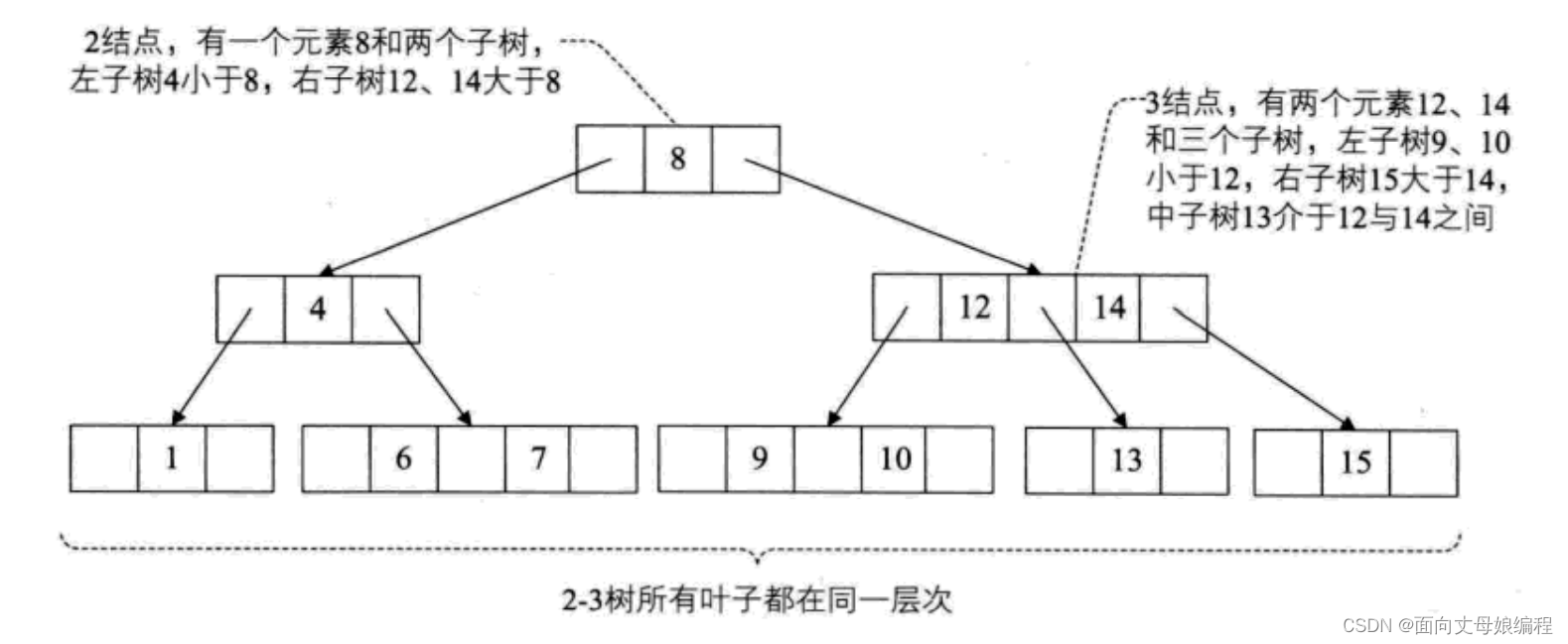
2-3树
2-3 树: 其中每一个节点都具有两个孩子(称为2节点)或者三个孩子(3节点)
- 一个2节点包含一个元素和两个孩子(或没有孩子), 且与二叉排序树类似, 左子树包含的元素小于该元素, 右子树包含的元素大于该元素. 不过, 与二叉排序树不同的是, 这个2节点要么没有孩子要有就有两个, 不能只有一个孩子.
- 一个3节点包含一大一小两个元素和三个孩子(或没有孩子), 和2节点一样, 要么没有孩子要么就有三个孩子. 左子树包含较小于元素的元素; 右子树包含较大于元素的元素. 中间子树包含介于两元素之间的元素
如图所示: 2-3树示意图
2-3 树插入实现
-
空树: 插入一个2节点即可
-
插入节点到一个2节点的叶子上.也就是说由于其本身就是一个元素, 所以只需要将其升级为3节点即可.
如图所示: 插入元素3

- 要往3节点中插入一个新元素. 因为3节点本身已经是2-3树的结点最大容量(已经有两个元素), 因此就需要拆分. 且将其中两元素或插入元素的三者中选择其一向上移动一层. 复杂的情况也正在于此.
第一种情况: 需要向左图中插入元素5。
经过遍历可得到元素5比8小比4大,因此它应该是需要插入在拥有6、7元素的3结点位置。问题就在于, 6和7结点已经是3结点,不能再加。此时发现它的双亲结点4是个2结点,因此考虑让它升级为3结点,这样它就得有三个孩子,于是就想到,将6、7结点拆分,让6与4结成3结点,将5成为它的中间孩子,将7成为它的右孩子,如图所示。

另一种情况: 需要向左图中插入元素11。
经过遍历可得到元素11比12、14小比9、10大,因此它应该是需要插入在拥有9、10元素的3结点位置。同样道理,9和10结点不能再增加结点。此时发现它的双亲结点12、14 也是个3结点,也不能再插入元素了。再往上看,12、14结点的双亲,结点8是个2结点。于是就想到,将9、10拆分,12、14也拆分,让根结点8升级为3结点.
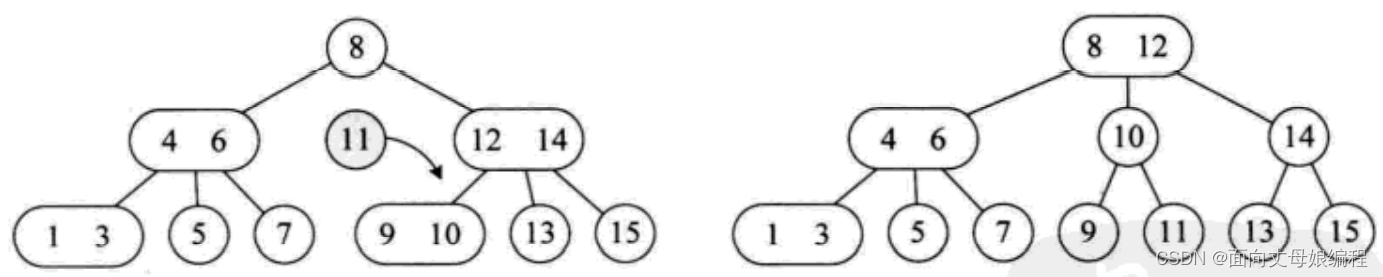
最后一种情况: 需要在左图中插入元素2。
经过遍历可得到元素2比4小、6比1大,因此它应该是需要插入在拥有1、3元素的3结点位置。与上例一样,你会发现,1、3结点,4、6结点都是3结点,都不能再插入元素了,再往上看,8、12结点还是一个3结点,那就意味着,当前我们的树结构是三层已经不能满足当前结点增加的需要了。于是将1、3拆分,4、6拆分,连根结点8、12也拆分.

通过这个列子, 我们发现2-3树插入的传播效应导致了根节点的拆分, 则树的高度就会增加.
2-3-4树的删除实现
-
所删除元素位于一个3节点的叶子节点,只需删除该节点即可, 不会影响整棵树的其它结构节点
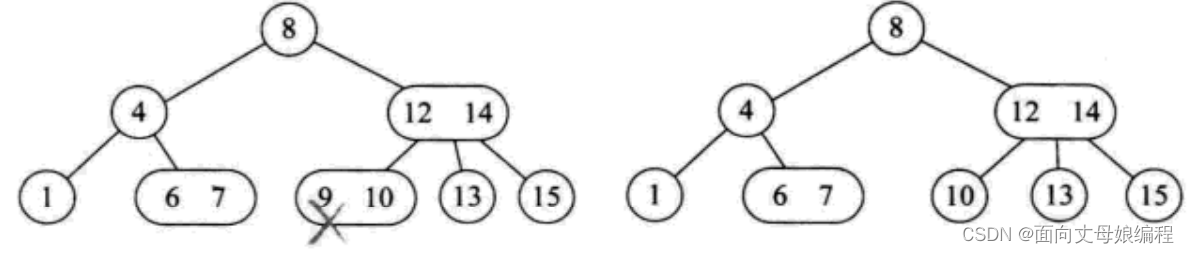
-
所删元素位于一个2节点的叶子节点,需要分四种情况讨论
情形一: 此节点双亲也是2节点
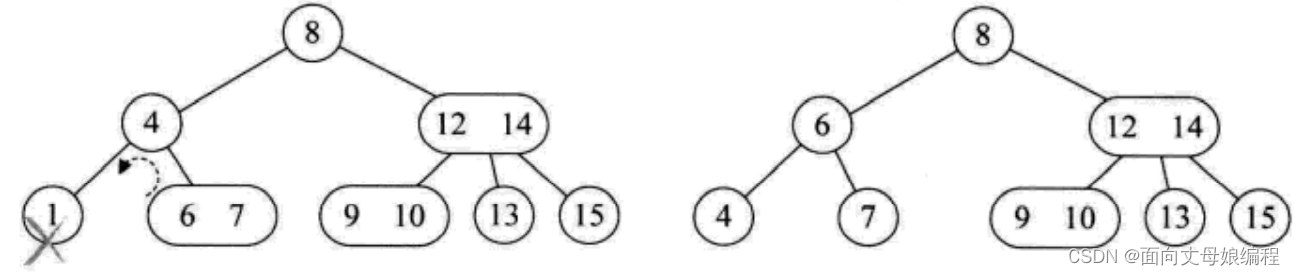
删除节点1,左旋即可,即6成为双亲,4成为6的左孩子,7是6的右孩子
情形二: 被删除节点是2节点, 右孩子也是2节点

删除节点4, 如果直接左旋会造成没有右孩子, 因此需要对整棵树变形: 节点7变成3节点, 那就的让比7稍大的元素8下来, 随即就得让比元素8稍大的元素9补充节点8的位置[中间图], 在采用左旋的方式变成右图
情形三: 此节点的双亲是一个3节点
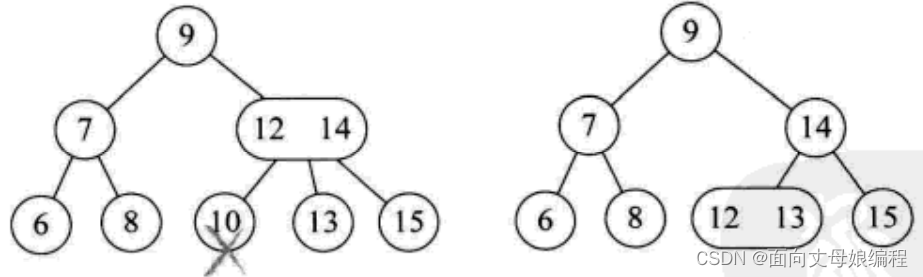
删除节点10, 意味着双亲12, 14这个节点不能成为3节点了, 于是将节点拆分, 并将13和12合并成为左右孩子
情形四: 当前树是一个满二叉树情况, 此时删除任何一个叶子都会使得整棵树不能满足2-3树定义
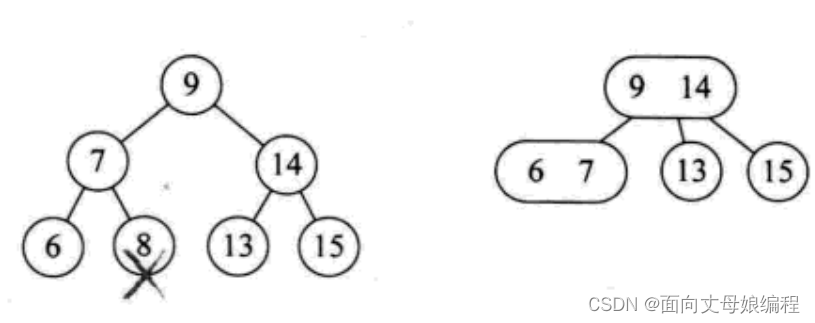
删除叶子节点8(删除任何一个节点都一样), 就不得不考虑将2-3树层数减少, 办法是将8的双亲和其左子树6合并为一个3节点, 再将14和9合并为3节点 -
所删除的元素位于非叶子的分支节点, 此时我们通常是将树按中序遍历得到此元素的前驱或后继元素, 考虑让他们来补位即可
-
删除的是分支节点
情形一: 删除的分支节点是2节点
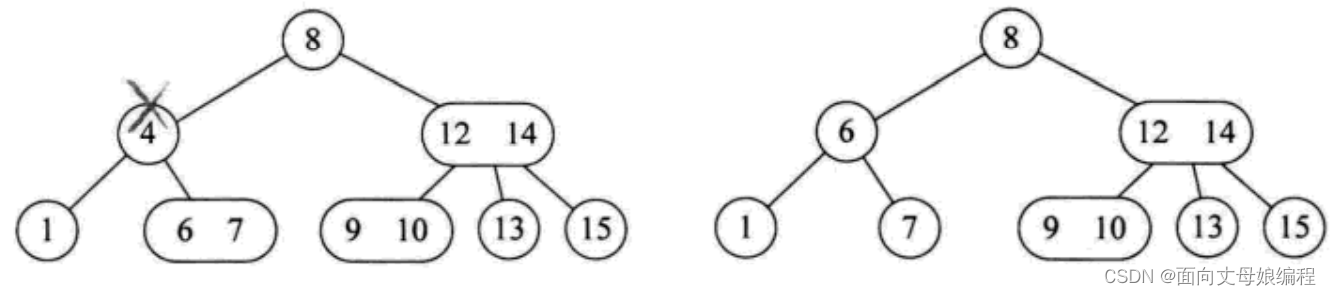
中序遍历结果: 1, 4, 6, 7, 8, 9, 10, 12, 13, 14, 15
要删除节点4的前驱是1后继是6, 由于6, 7是3节点, 只需要用6来补位即可情形二:删除的分支节点是3节点的某一元素
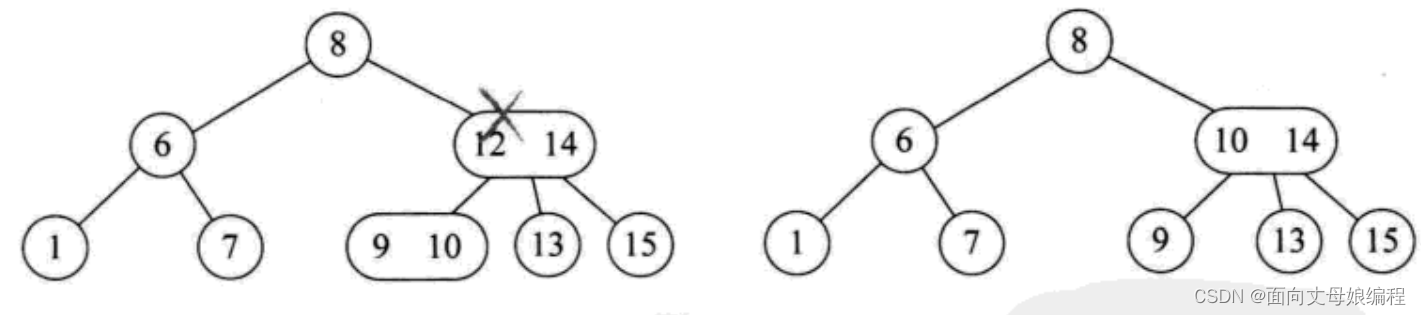
我们要删除12, 14节点的12. 显然应该是将是3节点的左孩子的10上升到删除位置合适.
2-3-4树
有了2-3树就会更好的理解2-3-4树, 它其实就是2-3树的扩展, 包括4节点的使用一个4节点包含小中大三个元素和四个孩子(或没有孩子)
- 一个4节点要么没有孩子, 要么具有4个孩子
- 如果4节点有孩子的话, 左子树包含小于最小元素的元素; 第二子树包含大于最小元素, 小于第二元素的元素; 第三子树包含大于第二元素, 小于最大元素的元素; 右子树包含大于最大元素的元素.
2-3-4插入
由于2-3-4树和2-3树是类似的,我们这里就简单介绍一下,如果我们构建一个数组为{7, 1,2,5,6,9,8,4,3}的2-3-4 树的过程,如下图所示。图1是在分别插入7、1、2时的结果图,因为3个元素满足2-3-4树的单个4结点定义,因此此时不需要拆分,接着插入元素5,因为已经超过了4结点的定义,因此拆分为图2的形状。之后的图其实就是在元素不断插入时最后形成了图7的2-3-4树。
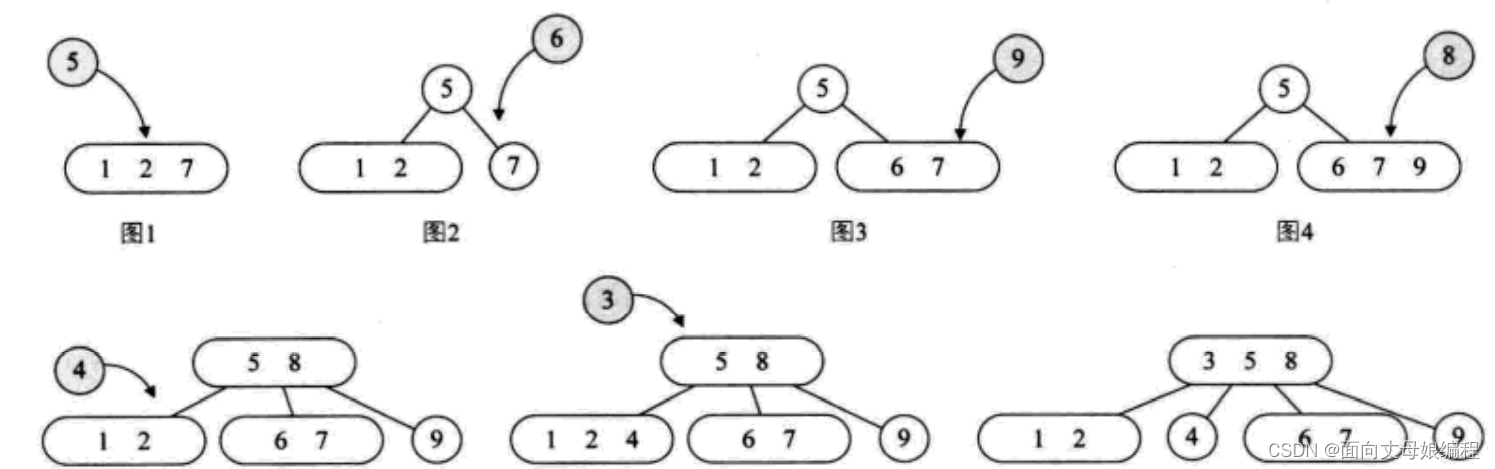
2-3-4树删除
删除顺序是: 1,6,3,4,5,2,9
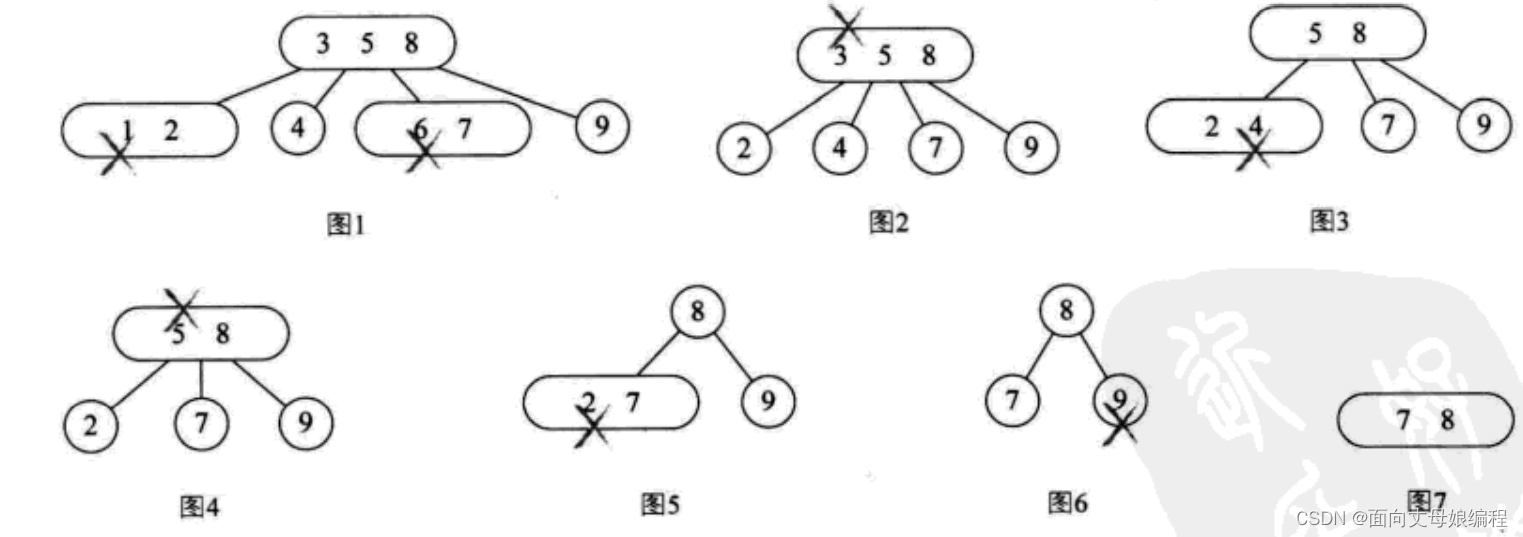
B树
B树(B-tree)是一种平衡的多路查找树,2-3树和2-3-4树都是B树的特例。结点最大的孩子数目称为B树的阶(order), 因此,2-3 树是3阶B树,2-3-4 树是4阶B树。
一个m阶的B树具有如下属性:
[m/2]表示不小于m/2的最小整数, 相当于m/2向上取整的效果
- 如果根结点不是叶结点,则其至少有两棵子树。
- 每一个非根的分支结点都有k-1个元素和k个孩子,其中[m/2]≤k≤m。
- 每一个叶子结点n都有k-1个元素,其中[m/2]≤k≤m。
- 所有叶子结点都位于同一层次。- 所有分支结点包含下列信息数据(n,A0,K1,A1,K2,A2,…, Kn,An),Ki(i=1,…,n)为关键字,且Ki<Ki+1 (i=1,2,…,n-1); Ai (i=0,2,…,n) 为指向子树根结点的指针,且指针Ai-1所指子树中所有结点的关键字均小于Ki(i=1,2, …,n),A0所指子树中所有结点的关键字均大于Kn, n.([m/2]-1≤n≤m-1)为关键字的个数(或n+1为子树的个数)。
2-3-4树时插入9个数后的图转成B树示意就如下图所示。左侧灰色方块表示当前结点的元素个数。

在B树上查找的过程是一个顺指针查找结点和在结点中查找关键字的交叉过程。比方说,我们要查找数字7,首先从外存(比如硬盘中)读取得到根结点3、5、8三个元素,发现7不在当中,但在5和8之间,因此就通过A2再读取外存的6、7结点,查找到所要的元素。
至于B树的插入和删除,方式是与2-3树和2-3-4树相类似的,只不过阶数可能会很大而已.
内存与外村交换数据频繁, 会造成时间效率上的瓶颈, B树是如何做到减少次数的呢
我们的外存,比如硬盘,是将所有的信息分割成相等大小的页面,每次硬盘读写的都是一个或多个完整的页面,对于一个硬盘来说,一页的长度可能是211到214个字节。
在一个典型的B树应用中,要处理的硬盘数据量很大,因此无法一次全部装入内存。因此我们会对B树进行调整,使得B树的阶数(或结点的元素)与硬盘存储的页面大小相匹配。比如说一棵B树的阶为1001 (即1个结点包含1000个关键字),高度为2,它可以储存超过10亿个关键字,我们只要让根结点持久地保留在内存中,那么在这棵树上,寻找某一个关键字至多需要两次硬盘的读取即可。这就好比我们普通人数钱都是一张一张的数,而银行职员数钱则是五张、十张,甚至几十张一数,速度当然是比常人快了不少。
通过这种方式,在有限内存的情况下,每一次磁盘的访问我们都可以获得最大数量的数据。由于B树每结点可以具有比二叉树多得多的元素,所以与二叉树的操作不.同,它们减少了必须访问结点和数据块的数量,从而提高了性能。可以说,B树的数据结构就是为内外存的数据交互准备的。
常见的搜索时间复杂度汇总
| 搜索结构 | 数据格式 | 时间复杂度 |
|---|---|---|
| 顺序查找 | 无要求 | O ( N ) O(N) O(N) |
| 二分查找 | 有序 | O ( l o g 2 N ) O(log_2{N}) O(log2N) |
| 二叉搜索树 | 无要求 | O ( l o g 2 N ) O(log_2{N}) O(log2N) |
| 二叉平衡树【AVLTree,RBTree】 | 无要求 | O ( l o g 2 N ) O(log_2{N}) O(log2N) |
| 哈希 | 无要求 | O ( 1 ) O(1) O(1) |
| 位图 | 无要求 | O ( 1 ) O(1) O(1) |
| 布隆过滤器 | 无要求 | O ( K ) O(K) O(K) 【K为哈希函数个数,一般K比较小】 |
以上常规的数据结构适合小规模数据搜索,如果数据量特别大,一次性无法加载到内存中,是用上述数据结构就不是很方便。比如:使用 二叉平衡树 搜索一个大文件
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yk2vNziI-1666369723122)(../resources/DataStructure/BTRee/二叉平衡树搜索大文件.png)]](https://img-blog.csdnimg.cn/e1e740b5e30d4b08b44ca7637cbc0b1a.png)
以上方法只是保存了需要查找的数据项部分,整体数据还是保存在磁盘中。
缺陷:
- 树的高度比较高
- 数据量特大的时候,不能一次放入内存。需要多次IO
优化方案:
- 降低树的高度
- 更换更好的硬件设备,提高硬件设备内存容量和IO速度
为此, BTree 横空出世,解决此痛点。一棵M阶(M>2)的多叉树平衡树称为B-树,可以是空树,它满足以下性质
- 空树也是B-树
- 根节点至少有两个孩子
- 每个非根节点至少有
Math.ceil(M/2)-1个关键字,至多有M-1个关键字,并且以升序排序 - 每个非根节点至少有
Math.ceil(M/2)个孩子节点,至多有M个孩子 key[i]和key[i+1]孩子的值介于key[i]和key[i+1]之间- 所有的叶子节点都在同一层
Math.ceil(-1.1) = -1.0 向上取整
Math.floor(-1.1) = -2.0 向下取整
Math.round(-1.4) = -1.0 四舍五入
Math.round(-1.6) = -2.0
BTree数据结构

孩子节点个数永远比关键字节点个数多一
插入过程中可能涉及到分裂
分裂的前提条件是:当关键字data个数>=M时【如果是一棵M路的多叉平衡树,那么关键字data个数必须<=M-1】
分裂规则:提取中间节点为父节点、左边单独构成一个节点、右边单独构成一个节点
为了展示方便,这里采用M=4的四叉树来演示
∵ M = 4 的四叉树 \because M=4的四叉树 ∵M=4的四叉树
∴ 一个节点只能存储 3 个关键字 \therefore 一个节点只能存储3个关键字 ∴一个节点只能存储3个关键字
这里为了后续方便【减少M-1的计算】,因此我们选择将
M=3设置为一个四叉树代码如下所示
public class BTree<K extends Comparable> {private static final int M = 3;static class BTreeNode<K> {// 存储关键字public K[] keys;// 当前孩子节点的父节点public BTreeNode<K> parent;// 存储孩子节点public BTreeNode<K>[] subs;// 记录该节点中关键字个数public int usedSize;public BTreeNode() {this.keys = (K[]) new Comparable[M];// 多给一个是为了好分裂this.subs = new BTreeNode[M + 1];}}
}
再定义节点个数的数组时候我们选择 M+1【M=3】 而不是 M【M=4】进行设置
四叉树
比如插入 {53, 139, 75, 49, 145, 36, 101} 元素
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c34hcsiJ-1666369723124)(../resources/DataStructure/BTree/插入53.png)]](https://img-blog.csdnimg.cn/77827a5b02fc4bcc9f786161cc0064e7.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V1Hg6e3D-1666369723124)(../resources/DataStructure/BTree/插入139.png)]](https://img-blog.csdnimg.cn/269a9d472c4841c3bfedbc442ed5a7f9.png)
插入75,由于139比它大,所以需要通过插入排序保证关键字有序
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f9sa2SsZ-1666369723125)(../resources/DataStructure/BTree/插入75.png)]](https://img-blog.csdnimg.cn/a7df3d6a7e1d40e99c179ecff3e3f1ce.png)
排序完之后在分裂
分裂方法
- 找到节点关键字域【数据域】的中间位置
- 给一个新节点,将中间数据的节点搬运到新节点;原来的节点就成为 “左节点”;右边数据单独一个节点
- 中间数据节点作为左右节点的父节点
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NeLJtYSp-1666369723125)(../resources/DataStructure/BTree/插入75分裂.png)]](https://img-blog.csdnimg.cn/5fca0af63a0b456589cf86f6c46a8b8a.png)
这里是一种特殊情况,第一次插入满的时候需要手动设置分裂后的根节点的关键字和子节点之间的关联关系。否则代码会引发后续的挪动数据和指向的时候空指针异常
具体空指针代码如下
BTreeNode<K> parent = cur.parent;
// 因为第一次插入满,那么 cur.parent 就是 NULL,控指针,那么对于 NULL 的引用就会报错
newBTreeNode.parent = parent;
// 开始移动父节点
int parentIndex = parent.usedSize - 1;
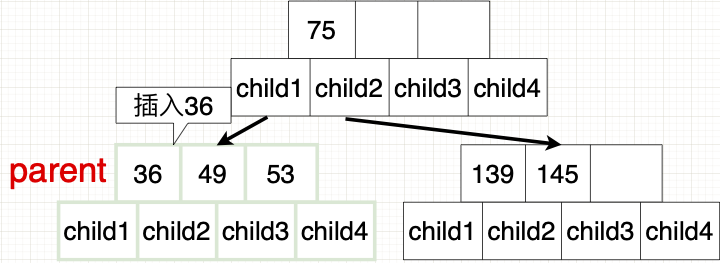
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2dF7dddC-1666369723126)(../resources/DataStructure/BTree/插入49.png)]](https://img-blog.csdnimg.cn/7654393ff02642198b2ab2d65738b24f.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2DndD0gd-1666369723126)(../resources/DataStructure/BTree/插入145.png)]](https://img-blog.csdnimg.cn/1936723fac40487cb2ae5124ad31548d.png)
这里就省略36的排序步骤直接显示插入结果
然后在分裂
- 发现该节点违反 B-树性质,所以需要分裂
- 中间关键字提上去放入父节点的关键字节点并排序
- 中间节点右边的节点搬运到一个新节点中,并插入到父节点的子节点中
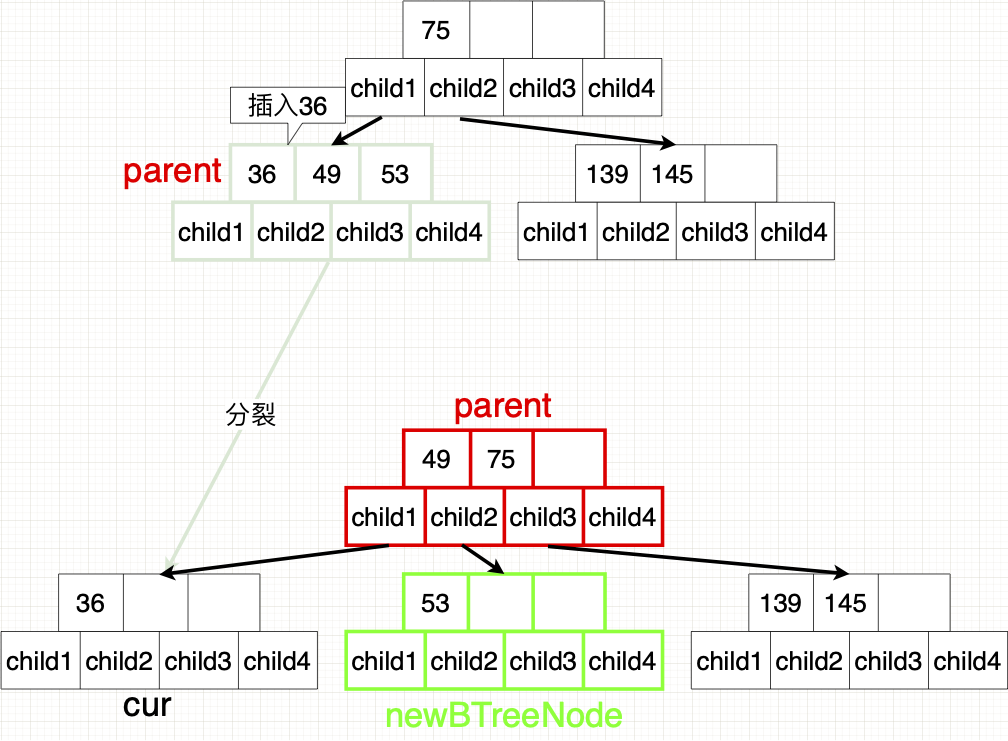
此时的分裂,由于不是第一次插入满。所以就不属于特殊情况而是正常的插入分裂。
- 先分裂出一个新节点
BTreeNode<K> newBTreeNode = new BTreeNode<>();- 记录插入之前的父节点
BTreeNode<K> parent = cur.parent;- 计算出中间数据节点下标,开始挪数据
int mid = cur.usedSize >> 1;- 先把右边的关键字数据
cur.keys[mid, cur.usedSize-1]挪到新分裂节点BTreeNode<>();同是需要挪动cur子节点,修改其子节点的指向新分裂的节点BTreeNode<>()- 跟新一下
cur, BTreeNode<>()节点的usedSize字段- 排序提上去的父节点
parent中的keys字段排序,并且注意其subs字段的排序- 最后递归判断当前节点的父节点是否满足B-树性质
现在对分裂过程有一定的初步了解了吧?我们再来看看一种连续分裂的情况
插入101,继续排序+分裂
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YV6ZpALp-1666369723128)(../resources/DataStructure/BTree/插入101.png)]](https://img-blog.csdnimg.cn/58803178f5f3456c80c0aedfd9a5d21a.png)
从上图可得知,也会发生 牵一发而动全身 的节点修改现象
每次插入的节点都是在叶子节点,插入完之后再手动调整B-树即可
分裂根节点会导致树的高度+1;分裂非根节点会使得树 “变宽”
B-树的存储量
假设 M=1023 ,一个节点能存储 1023 个关键字,1024 个节点
第一层: 1023
第二层: 1023 × 1024 = 10 _ 47552 1023 \times 1024 = 10\_47552 1023×1024=10_47552
第三层: $ 1023 \times 1024 \times 1024 = 10_7269_3248$
计算一下之后就会发现,M=1023 的B-树已经达到了很大的数据存储
BTree实现
package bTree;public class BTree<K extends Comparable> {private static final int M = 3;static class BTreeNode<K> {// 存储关键字public K[] keys;// 当前孩子节点的父节点public BTreeNode<K> parent;// 存储孩子节点public BTreeNode<K>[] subs;// 记录该节点中关键字个数public int usedSize;public BTreeNode() {this.keys = (K[]) new Comparable[M];// 多给一个是为了好分裂this.subs = new BTreeNode[M + 1];}}public BTreeNode<K> root;public boolean insert(K key) {// 1.如果 B-树 中没有数据【模拟搜索二叉树插入方式】if (root == null) {root = new BTreeNode<>();root.keys[0] = key;++root.usedSize;return true;}// 2.B-树不为空,我们先查找B-树中是否有我们要找的key值Pair<BTreeNode<K>, Integer> pair = findRoot(key);if (!pair.getVal().equals(-1)) {// 说明找到了该节点,所以不能插入return false;}// 3.说明这个 key 不存在,可以插入BTreeNode<K> parent = pair.getKey();int index = parent.usedSize - 1;for (; index >= 0; index--) {if (parent.keys[index].compareTo(key) >= 0) {parent.keys[index + 1] = parent.keys[index];} else {break;}}parent.keys[index + 1] = key;++parent.usedSize;// 因为每次都是插入的叶子节点,所以不需要处理if (parent.usedSize >= M) {// 父节点存储满了,就进行分裂split(parent);}return true;}/*** 分裂逻辑** @param cur*/private void split(BTreeNode<K> cur) {BTreeNode<K> newBTreeNode = new BTreeNode<>();// 1.先存储当前需要分裂节点的父节点BTreeNode<K> parent = cur.parent;// 2.开始挪数据int mid = cur.usedSize >> 1;int i = mid + 1;int j = 0;for (; i < cur.usedSize; i++) {newBTreeNode.keys[j] = cur.keys[i];newBTreeNode.subs[j] = cur.subs[i];// 新分裂newBTreeNode的孩子节点subs指向父节点newBTreeNode【叶子节点的话 subs 就为空】if (newBTreeNode.subs[j] != null) {newBTreeNode.subs[j].parent = newBTreeNode;}++j;}// 多拷贝一次cur孩子节点subs给新分裂节点新分裂节点并修改指向newBTreeNode.subs[j] = cur.subs[i];if (newBTreeNode.subs[j] != null) {newBTreeNode.subs[j].parent = newBTreeNode;}// 更新新分裂新节点的有效数据newBTreeNode.usedSize = j;// 更新当前节点cur的有效数据【-1是将来要提取到父节点的key】cur.usedSize = cur.usedSize - newBTreeNode.usedSize - 1;// 处理特殊情况if (cur == root) {root = new BTreeNode<>();root.keys[0] = cur.keys[mid];root.subs[0] = cur;root.subs[1] = newBTreeNode;root.usedSize = 1;cur.parent = root;newBTreeNode.parent = root;return;}//新分裂节点newBTreeNode指向父节点parentnewBTreeNode.parent = parent;// 开始移动父节点int parentIndex = parent.usedSize - 1;K curMidVal = cur.keys[mid];for (; parentIndex >= 0; parentIndex--) {if (parent.keys[parentIndex].compareTo(curMidVal) >= 0) {parent.keys[parentIndex + 1] = parent.keys[parentIndex];parent.subs[parentIndex + 2] = parent.subs[parentIndex + 1];} else {break;}}// 当前节点提升到父节点中parent.keys[parentIndex + 1] = curMidVal;// 父节点指向新分裂的子节点parent.subs[parentIndex + 2] = newBTreeNode;++parent.usedSize;// 继续判断if (parent.usedSize >= M) {split(parent);}}private Pair<BTreeNode<K>, Integer> findRoot(K key) {BTreeNode<K> cur = root;BTreeNode<K> parent = null;while (cur != null) {int i = 0;while (i < cur.usedSize) {if (cur.keys[i].compareTo(key) == 0) {// 返回当前找到的 节点和下标return new Pair<>(cur, i);} else if (cur.keys[i].compareTo(key) < 0) {++i;} else {break;}}parent = cur;cur = cur.subs[i];}// 返回找不到的该节点的 父节点【用-1来代表该节点是父节点 】return new Pair<>(parent, -1);}// "中序" 遍历如果有序,可以证明这个B-树是对的,但并不是只要一棵树中序遍历有序就能称为 B-树public void inorder(BTreeNode root) {if (root == null) return;for (int i = 0; i < root.usedSize; i++) {inorder(root.subs[i]);System.out.print(root.keys[i] + " ");}inorder(root.subs[root.usedSize]);}
}测试
public class Test {private static void BTreeTest() {BTree<Integer> bTree = new BTree<>();int[] arr = {53, 139, 75, 49, 145, 36, 101};for (int i:arr ) {bTree.insert(i);}bTree.inorder(bTree.root);}public static void main(String[] args) {BTreeTest();}
}36 49 53 75 101 139 145
BTree性能分析
首先之前的二叉搜索树的时间复杂度如何计算的呢?我们回顾一下。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Rc6wcHz1-1666369723129)(../resources/DataStructure/BTree/二叉搜索树时间复杂度.png)]](https://img-blog.csdnimg.cn/bdf4d53612e640ddb78b3a93d5662357.png)
在最好的情况下是 O ( l o g 2 N ) O(log_2{N}) O(log2N) ,最坏是 O ( N ) O(N) O(N) 。而二叉搜索树的插入删除都是在查找基础上实现的,B-树也不例外。所以查找的效率会影响B-树的效率。二叉搜索树每次只能根据值判断两个节点,M阶B-树 根据值能判断 M 个节点,然后在对应的节点中在进行 二分查找 效率会很高。
∵ 一棵度为 N 的 M 路 B − 树 \because 一棵度为 N 的M路B-树 ∵一棵度为N的M路B−树
∴ 每个节点关键字数组存储的的关键字个数 : [ M 2 − 1 , M − 1 ] \therefore 每个节点关键字数组存储的的关键字个数: [{M \over 2} - 1, M-1] ∴每个节点关键字数组存储的的关键字个数:[2M−1,M−1] 【 m 2 m \over 2 2m需要向上取整】
∴ 每个节点数组存储的节点个数 : [ M 2 , M ] \therefore 每个节点数组存储的节点个数: [{M \over 2}, M] ∴每个节点数组存储的节点个数:[2M,M] 【 m 2 m \over 2 2m需要向上取整】
假设 M = 3 , M 2 = 1.5 ,向上取整为 2 假设M=3,{M \over 2} = 1.5,向上取整为2 假设M=3,2M=1.5,向上取整为2
3路B-树最少存储1个关键字,最多存储2个关键字
3路B-树最少存储2个关节点,最多存储3个节点
B-树上的操作通常由存取磁盘的时间和CPU计算时间这两部分组成。B-树上大部分基本操作所需访问磁盘的次数均取决于查找效率,查找效率取决于树高。因此关键字个数相同的情况下,与二叉搜索树相比,B-树对于磁盘的IO次数更少。与高速的CPU计算相比,磁盘IO会慢很多,所以可以忽略CPU计算时间,只分析磁盘的访问次数【磁盘访问次数 * 1次磁盘IO的时间 = 总耗费时间】
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gceuhdyA-1666369723129)(../resources/DataStructure/BTree/HDD.png)]](https://img-blog.csdnimg.cn/e349f236ed834bc7a761025c29dd85f8.png)
索引一般保存在文件当中,检查索引需要耗费磁盘IO,磁盘IO效率和内存的效率完全不是一个数量级。
每次读取数据的时候,磁盘就会同步同轴转动,磁头支架上的磁头就会在磁道上读取数据,磁头不能转动但可以沿磁盘半径方向做斜切运动,每个磁头负责一个磁盘片。
盘片被划分为多个同心环,圆心是盘片中心,每个同心环被称为磁道,所有半径相同的磁道组成一个柱面,每个柱面又被切割为多个小段,每一小段称为一个扇区,扇区是存储数据的最小单元
需要磁盘读取数据的时候,系统会给磁盘一个逻辑地址,磁盘的控制电路就把逻辑地址转换为对应的物理地址再读取扇区的数据,步骤如下:
- 寻道:磁头需要找到对应的移动到对应磁道
- 旋转:将盘面旋转到磁头目标对应的扇区下
局部性原理和磁盘预读
由于磁盘的机械特性,读取速度慢于SSD很多倍,更是和慢于内存RAM的几个数量级。所以通常会采取减少IO次数来达到提升读取效率。为了达到这个目的,磁盘并非是按需读取,而是每次都预读一些数据。即是只需要1字节数据,程序也会连续向后读取很多数据预存到RAM内存中
局部性原理: 当程序的某一块数据需要用到的时候并不是仅用那一块,而是附近的扇区数据也会用到,程序运行期间用到的数据比较集中。因此磁盘会顺序读取【顺序读取不需要寻道,只需要很少的旋转盘面时间】多的数据加入缓存中,因此对于局部性程序来说,可以短暂提高一定的IO效率
预读的长度一般为页【page】的整倍数。页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,每个存储块称为一页(在许多操作系统中,页得大小通常为4k),主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
这里为介绍BTree应用——MySQL存储引擎埋伏笔
为了简述方便,这里用 t 代表每个(根除外)内部节点的最小度数 [ M 2 , M ] [{M \over 2}, M] [2M,M],树的高度范围 [ L o g t M 2 , L o g t M Log_{t}{M \over 2}, Log_{t}{M} Logt2M,LogtM],树的高度也就决定着查找的效率
∵ 2 32 = 42 _ 9496 _ 7296 \because {2}^{32}=42\_9496\_7296 ∵232=42_9496_7296
∴ l o g 2 42 _ 9496 _ 7296 = 32 \therefore log_{2}{42\_9496\_7296} = 32 ∴log242_9496_7296=32
| 数据结构 | 节点个数N | 查找次数 |
|---|---|---|
| 二叉平衡树 | 10000_0000_0000 | l o g 2 10000 _ 0000 _ 0000 = 39.86313713864835 ≈ 40 log_2{10000\_0000\_0000} = 39.86313713864835 \approx 40 log210000_0000_0000=39.86313713864835≈40 |
| B-树 | 10000_0000_0000 | 如果M=1024则 l o g M 2 10000 _ 0000 _ 0000 = 4.4292374598498165 ≈ 5 log_{M \over2}{10000\_0000\_0000} = 4.4292374598498165 \approx 5 log2M10000_0000_0000=4.4292374598498165≈5 |
发现,数据量越大之间的差距越大。对于1万亿级别的数据,二叉平衡树需要查找40次,B-树只需要查找5次就可以定位到该节点。然后再使用二分查找就可以快速定位到元素。
M=1024,二分查找+B-树搜索的总效率: l o g 2 1024 + l o g t N log_{2}{1024} + log_{t}{N} log21024+logtN
此时会有天才问:二分查找不也是在读取磁盘IO嘛?而且还是512次的磁盘IO!!!
其实二分查找也只是查找1204个数据,完全可以放在内存中交给CPU进行快速查找,B-树查找对于万亿级别的数据,10亿个整数就需要 10 _ 00000000 × 4 ÷ 102 4 3 = 3.725290298461914 ≈ 4 G 10\_00000000 \times 4 \div 1024^3 = 3.725290298461914 \approx 4G 10_00000000×4÷10243=3.725290298461914≈4G,1w亿整数大约需要 4000G内存 ,这就很恐怖了。
因此我们计算B-树的复杂度的时候可以治考虑磁盘的IO而不是CPU的计算,对于一个 2GHz 的CPU,每秒进行2K次计算,512次计算简直不在话下,更何况现在i9-12900ks到达了3.4/5.5GHz;Ryzen9 5950x 3.4/5.0GHz
此时又有天才会问:二叉树即然不行,它的进化品种红黑树的难道也不行?
试想一下,1w亿的数据放入红黑树,它的树高会是B-树的8倍,8倍的磁盘IO效率不说还会因为红黑树父子节点无法充分利用磁盘的局部性原理进行预读缓存大量程序运行期间所需要的数据。结合来看,红黑树的IO效率简直不能和B-树对比
B-树删除
删除会很复杂,我暂且也还不会。思想是:分裂,合并和转移来保持
B+树
尽管前面我们已经讲了B树的诸多好处,但其实它还是有缺陷的。对于树结构来说,我们都可以通过中序遍历来顺序查找树中的元素,这一切都是在内存中进行。
可是在B树结构中,我们往返于每个结点之间也就意味着,我们必须得在硬盘的页面之间进行多次访问,如图所示,我们希望遍历这棵B树,假设每个结点都属于硬盘的不同页面,我们为了中序遍历所有的元素,页面2-→页面1→页面3-→页面1→页面4-页面1-→页面5。而且我们每次经过结点遍历时,都会对结点中的元素进行一一次遍历,这就非常糟糕。有没有可能让遍历时每个元素只访问一次呢?
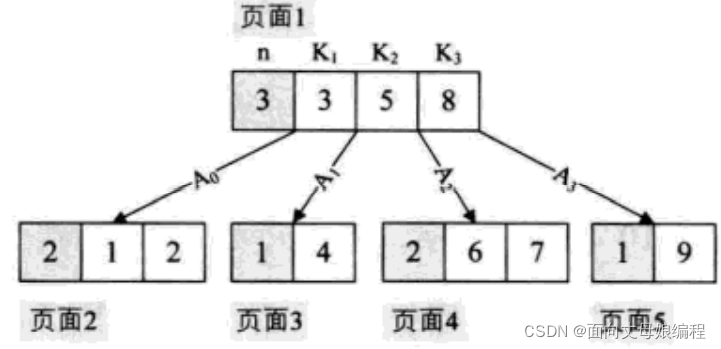
B+树是应文件系统所需而出的一种B树的变形树,注意严格意义上讲,它其实已经不是定义的树了。在B树中,每一个元素在该树中只出现一次,有可能在叶子结点上,也有可能在分支结点上。而在B+树中,出现在分支结点中的元素会被当作它们在该分支结点位置的中序后继者(叶子结点)中再次列出。另外,每一个叶子结点都会保存一个指向后一叶子结点的指针。
例如图所示,就是棵B+树的示意,灰色关键字即是根结点中的关键字在叶子结点再次列出,并且所有叶子结点都链接在一起。
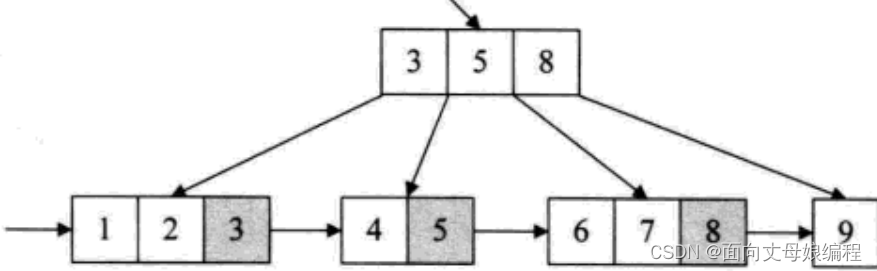
一棵m阶的B+树和m阶的B树的差异在于
- 有n棵子树的结点中包含有n个关键字
- 所有的叶子结点包含全部关键字的信息,及指向含这些关键字记录的指针,叶子结点本身依关键字的大小自小而大顺序链接
- 所有分支结点可以看成是索引,结点中仅含有其子树中的最大(或最小)关键字
这样的数据结构好处在于, 如果要随机查找, 我们就从根节点出发, 与B树的查找方式相同, 只不过即使在分支节点找到了待查找的关键字, 他也只是用来索引的, 不能提供实际记录的访问, 还是需要到达到包含此关键字的终端节点.
如果我们是需要从最小关键字进行从小到大的顺序查找,我们就可以从最左侧的叶子结点出发,不经过分支结点,而是延着指向下一叶子的指针就可遍历所有的关键字。
B+树的删除插入操作也和B树类似, 只不过插入和删除的元素都是在叶子节点上进型而已
B-树有很多变种,B+树是B-树的一种最常用的变形,关键字数据全放在叶子节点,每个节点存储的关键字个数和自节点个数相等,叶子节点挂单链表且单链表数据有序,每个单链表的尾节点再指针串起来构成一个单链表
定义与B-树相同除了以下不同
-
非叶子节点的节点数个关键字个数相同
B-树节点中关键字和子节点个数不同,但是都有各自规定的上限,所以每个节点的内存大小相同
B+树由于把数据全部存放在了叶子节点挂在的链表上,因此叶子节点和非叶子内存大小不同
一般来说,B+树更适合做数据的索引存储结构,根据上文中对于页的简介,数据库巧妙的利用了局部性原理和磁盘的顺序读写效率高的特性,将一个节点设置为一个页的大小,这样每个节点只需要一次IO就可以完全载入
-
非叶子节点的节点
p[i]指向关键字值属于[k[i], k[i+1]]的子树 -
为所有的叶子节点增添一条单链表指针
访问到某一节点之后就可以通过该节点所在的单链表访问全部数据
-
所有关键字只在叶子节点出现
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N0QaF23Z-1666370242899)(../resources/DataStructure/BTree/B+树.png)]](https://img-blog.csdnimg.cn/0284cc1338214a629376e8e1a8a0e4ed.png)
B+树的搜索和B-树相同。区别只在于B-树可以在所有节点搜索命中,B+树只在叶子节点命中。两者之间的性能也等价于在关键字全集做一次二分查找;也可以通过尾节点指针顺序访问别的节点的数据域
B+树特性:
-
所有关键字都出现在叶子节点【稠密索引】,且链表中的数据是有序的
-
不可能在非叶子节点命中
-
非叶子节点相当于叶子节点的稀疏索引,叶子节点相当于存储数据的数据层
-
更适合做文件系统
-
B+树分裂: 当一个节点满时,分裂一个新节点,把满节点的 1 2 1 \over 2 21 的数据拷贝被新分裂的节点,最后在父节点中增加分裂节点的新指针
p[i],再像 B- 树一样递归判断父节点即可B+树分裂只影响父节点和原节点,不会影响兄弟节点所以不需要增加兄弟节点之间的指针
B*树
B*树相当于B+树的变形,在B+树的非根节点和非叶子节点增加一个指向兄弟节点的指针
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z25jX3nY-1666370242900)(../resources/DataStructure/BTree/B*树.png)]](https://img-blog.csdnimg.cn/1e8c97105c2f4bd08409187f2ffe1152.png)
B*树特性:
-
B*树定义了非叶子节点关键字个数至少为 2 3 M {2 \over 3}M 32M ,即每一个节点的使用率从B+树的 1 2 1 \over 2 21 提升到 2 3 2 \over 3 32
-
B*树分裂: 当一个节点满时,下一个兄弟节点未满,就将一部分数据拷贝给兄弟节点,再在原节点中插入关键字,最后修改父节点中兄弟节点的指针【因为兄弟节点关键字范围变动】;下一个兄弟节点满了,则新分裂一个节点,原节点和兄弟节点个拷贝 1 3 1 \over 3 31 的数据到新节点中,父节点中再新增新分裂节点的关键字指针
B*树的分配新节点的概率比B+树低,空间利用率更高
简短的总结
- B-树: M路搜索树,每个节点存储 [ M 2 , M ] [{M \over 2}, M] [2M,M] 个关键字, [ M 2 − 1 , M − 1 ] [{M \over 2}-1, M-1] [2M−1,M−1] 个关键字,关键字进出现一次,非叶子节点也可以命中
- B+树: B-树基础上,叶子节点增加链表存储关键字数据作为稠密索引,非叶子节点作为叶子节点的稀疏索引,关键字只能在叶子节点命中
- B*树: B+树基础上,非叶子节点和非根节点增加兄弟节点指针,将节点的存储利用率从之前的B-树的 1 2 1 \over 2 21 提升到 2 3 2 \over 3 32
B树应用
索引
B-树最常见的就是制作索引。用来实现快速查找功能。MySQL官方对索引的定义为: 索引[index]是帮助MySQL高效获取数据的数据结构
我们都知道数据库的最重要功能之一就是查询。我们希望数据能够查询的足够快,因此数据库的设计者会从查询算法上进行优化。最基本的查找算法就是顺序查找, O ( N ) O(N) O(N) 的效率是在是太慢了,试想一下上文介绍的 1000亿数据的查找,在不考虑内存的情况得下cpu也计算1000亿次 ,这明显的耗费CPU资源。好在科学家们发明了更多的算法,将时间复杂度从 O ( N ) O(N) O(N) 提升到 O ( l o g 2 N ) O(log_{2}{N}) O(log2N) 二分查找(binary_ search)、 O ( l o g 2 N ) O(log_{2}{N}) O(log2N)二叉树查找(binary_tree_search)等。但是仔细发现之后会得知:这些数据的查找都是基于一定的组织结构:二分查找需要数据有序、二叉树查找需要在二叉搜索树上进行。但数据在存放的时候并不会完全满足各种数据结构,因此数据库还会维护着特定查找算法的数据结构,这些数据结构以某种方式指向「引用」数据,因此就可以在特定的数据结构上是先高级的查找算法。这种数据结构就叫做索引。
MySQL的索引
MySQL中索引属于存储引擎级别的概念,不同存储引擎对索引的实现方式是不同的
SHOW ENGINES;
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A9MfIcyA-1666370694061)(../resources/DataStructure/BTree/存储引擎.png)]](https://img-blog.csdnimg.cn/2f296f3616584038bc313d0ea77367dd.png)
索引是基于表的,而不是基于数据库
我们在查看一下MySQL的数据库状态
SHOW GLOBAL STATUS;
查询太多了,我们可以只查询我们想要的数据列
mysql> SHOW GLOBAL STATUS LIKE "innodb_page_size";
+------------------+-------+
| Variable_name | Value |
+------------------+-------+
| Innodb_page_size | 16384 |
+------------------+-------+
1 row in set (0.00 sec)
MyISAM
MyISAM引擎 是MySQL5.5.8之前的默认存储引擎,不支持事务,不支持全文检索,使用B+树作为索引结构。叶节点的data存储的是数据记录的地址
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qWcukYOA-1666370565117)(../resources/DataStructure/BTree/MyISAM主索引.png)]](https://img-blog.csdnimg.cn/7ed6224499d140ee8c12c1bcb79bc683.png)
上图以 id 为主键,MyISAM 存储引擎的示意图。可以看出 MyISAM 的叶子节点只存储数据记录的地址。它的主索引和辅助索引的结构没有任何区别,只是 主索引要求Key唯一;辅助索引key可重复。如果想利用 name 字段做辅助索引,则结构如下
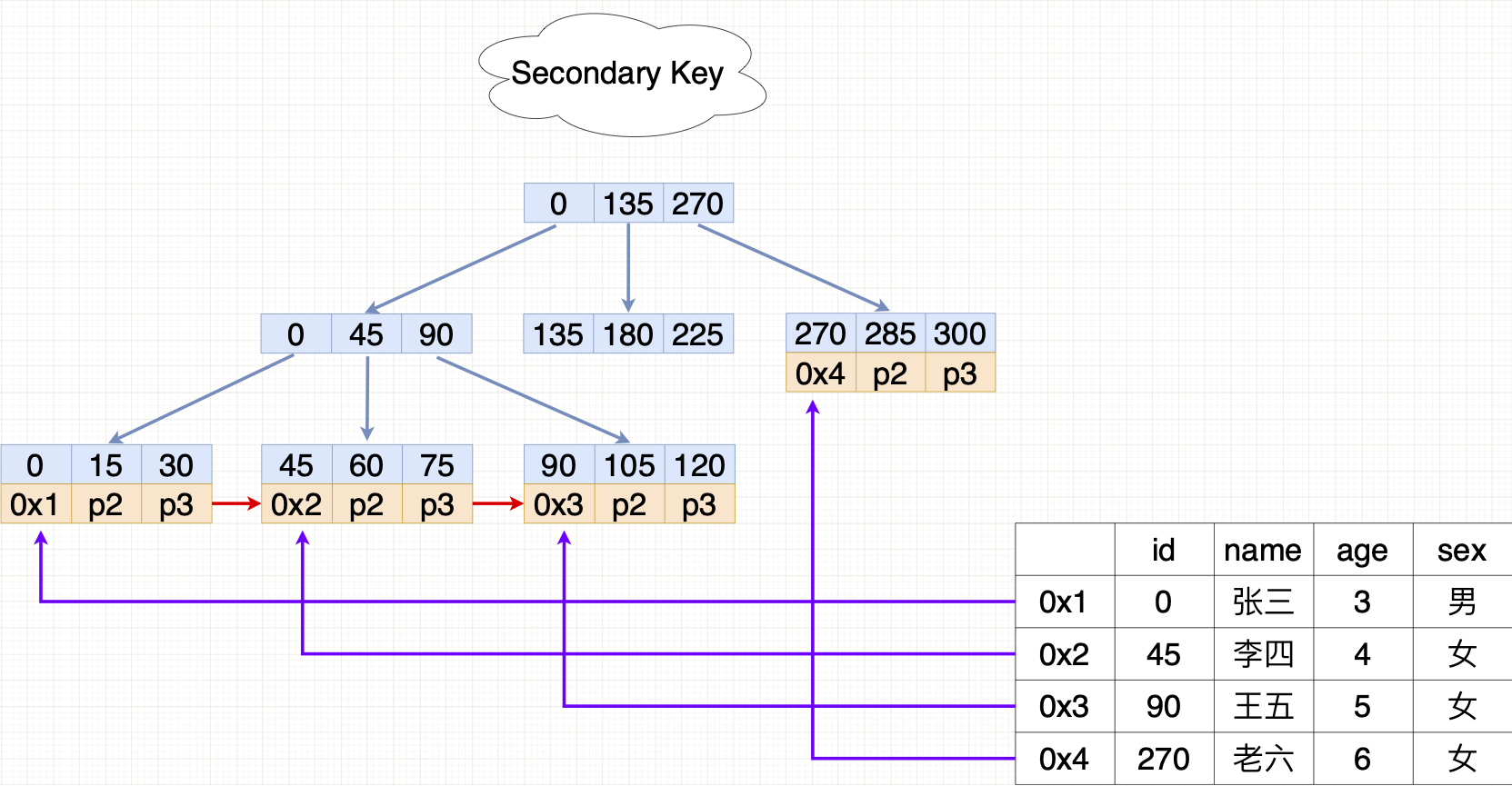
因此对于B+树,叶子节点存储数据的地址。如果能找到指定的主键Key,则去对应的磁盘上以找出来的data值作为地址,再找数据本身读取相应数据记录。
这种索引叫做 非聚集索引
Innodb
Innodb支持事务,MySQL5.5.8之后是MySQL默认存储引擎。Innodb支持B+树索引,全文索引,哈希索引
Innodb 使用B+树索引的时候与MyISAM不同
B+树索引区别如下
-
Innodb本身就是索引文件,叶子节点存储的是数据本身,节点中的key就是数据库表中的主键;MyISAM是索引和文件分离的,叶子节点存储的是数据记录的地址

所以Innodb必须要求有主键,MyISAM可以没有。如果没有显示指定,MySQL会自动选择一个可以自动标识数据记录的列作为主键;如果没有合适的列,则会自动为Innodb生成一个隐含的6字节长整型字段为主键
-
Innodb辅助索引的data域存储的都是主键的值而不是地址

Innodb这种叶子节点包含了完整的数据记录,这种索引叫做
聚集索引聚集索引搜索主键非常高效;辅助索引需要搜索两遍,第一遍从辅助索引获取到主键,第二遍用这个主键去主索引中查找获取数据
图
概念
图
图: 是由顶点集合和顶点关系组成的一种数据结构: G={V,E}
-
有向图: Path(x, y),x到y是一条双向通路,即Path(x, y)是无方向的
-
无向图: Path<x, y>,x到y是一条单向通路,即Path<x, y>是有方向的
G: 图(Graph)
V: 顶点(Vertex)【图中节点称为顶点,第i个顶点记做vi】
E: 边(Edge)【两个顶点vi和vj相关联,称作顶点vi和顶点vj之间有一条边,记做ek】
ek=(vi, vj) 或者<vi, vj>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-T48lnjG1-1666710692064)(../resources/DataStructure/Graph/有向无向图.png)]](https://img-blog.csdnimg.cn/2da48af45faf40ffa75b2705cd433b1f.png)
有向图: G1,G2【树一种特殊的图,但图不一定是树】
无向图: G3,G4
完全图
- 无向完全图: 在有 N 个定点的无向图中,若有 N × ( N − 1 ) 2 {N \times (N-1)} \over 2 2N×(N−1) 条边【任意两点之间有且只有一条边】。上图G1
- 有向完全图: 在有 N 个定点的有向图中,若有 N × ( N − 1 ) N \times (N-1) N×(N−1) 条边【任意两点之间有且只有两条方向相反的边】。上图G4
无向图边的计算方式:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AMI2TeZK-1666710692067)(../resources/DataStructure/Graph/完全图.png)]](https://img-blog.csdnimg.cn/94256ca1042348b9acf9cb66522d140d.png)
有向图每次连出去的线是无向图的2倍,所以依据无向图像等差公式推出之后乘以2即可
邻接顶点
- 无向图: e(0, 1)是G1中的一条边,0和1互为邻接顶点。e(0, 1)依附于顶点0和1
- 有向图: e(0, 1)是G4中的一条边,0邻接到1,1邻接到0。e(0, 1)与顶点0和顶点1相关联
顶点的度
顶点v的度是指与之相关联的边的条数,记做deg(v)
- 无向图: deg(v)=indeg(v)=outdeg(v)【顶点的度=顶点的出度=顶点的入度】。G1中 deg(0) = 3
- 有向图: deg(v)=indeg(v)+outdeg(v)【顶点的度=顶点的出度+顶点的入度】。G4中 deg(0) = 6
路径
从顶点 v(i) 出发,有一组边可以到达顶点 v(j),则 v(i) 到 v(j) 得定点序列称为 v(i) 到 v(j) 的路径
路径长度
- 带权值: 该路径上权值总和
- 不带权值: 该路径上边的条数
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2FI9F1fG-1666710692067)(../resources/DataStructure/Graph/路径长度.png)]](https://img-blog.csdnimg.cn/8bd6051ca858437ea8c36f0a25ba249f.png)
简单路径与回路
- 简单路径: v(i) 到 v(j) 路径上的顶点不重复【G1中0,1,2,3】
- 回路: v(i) 和 v(j) 路径上第一个顶点和最后一个顶点重复【G1中0,1,2,1】
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-P9fNcGUa-1666710692068)(../resources/DataStructure/Graph/简单路径与回路.png)]](https://img-blog.csdnimg.cn/f824a05e09484677a0670268b686e109.png)
子图
G1/G3子图的V集合和E集合均被G1/G3包含,所以是G1/G3子图
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jPUihndZ-1666710692070)(../resources/DataStructure/Graph/子图.png)]](https://img-blog.csdnimg.cn/0e2c9ad4e22144c891eb14ad5958bd2d.png)
连通图
在 无向图 中,如果 v(i) 到 v(j) 有路径,就说明 v(i) 和 v(j) 是连通的。如果无向图中任意一顶点都是连通的。则是连通图
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YRbESeoa-1666710692071)(../resources/DataStructure/Graph/连通图.png)]](https://img-blog.csdnimg.cn/9b233603b8fd45c790a9115bb982b7e5.png)
强连通图
在 有向图 中,如果每一个 v(i) 到 v(j) 之间都有路径并且 v(j) 到 v(i) 也都有路径。则是强连通图。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hnwOBloN-1666710692072)(../resources/DataStructure/Graph/强连通图.png)]](https://img-blog.csdnimg.cn/97cd75ca64f24f19a52513bdf436ec62.png)
生成树
一个连通图的最小连通子图称作该图的生成树。有N个顶点的连通图生成树有N个顶点,N-1条边
连通图中的每棵生成树,都是原图的极大无环子图。从生成树中删除任何一边,生成树不在连通;加入任何一边,就会形成回路
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3nR9dCuc-1666710692073)(../resources/DataStructure/Graph/G1生成树.png)]](https://img-blog.csdnimg.cn/ed01ce84167b498eb77235cc060281d7.png)
数据结构
图中只有节点和边,节点很好保存,只需要一段连续的内存空间即可。如何保存节点之间的关系【边】呢?
邻接矩阵
边与边之间的关系只有联通或不连通两种关系,即0或1。因此先用一个数组存储节点;二维数组在存储节点之间的关系
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oLX6uNYd-1666710692074)(../resources/DataStructure/Graph/邻接矩阵.png)]](https://img-blog.csdnimg.cn/82ef5f40be29480c8785054aea612954.png)
特性
-
无向图的邻接矩阵对角线对称,顶点i所在某一行之和或者某一列之和就是顶点度
-
有向图邻接矩阵不一定对称,顶点i所在的某一行加上某一列就是顶点的度
-
不带权值用 0 代表不连通;带权值用 ∞ 代表不连通
优缺点
- 优点:用邻接矩阵优点是可以快速判断两个节点是否连通
- 缺点:当顶点比较多,边比较少的时候,存储了大量0成为关系的矩阵,比较浪费空间,并且两点之间路径不好计算
package Graph;import java.util.Arrays;/*
邻接矩阵*/
public class GraphByMatrix {private char[] arrayV;// 定点数组private int[][] matrix;//邻接矩阵private boolean isDirect;// 是否为有向图/*** size: 顶点个数** @param size* @param isDirect*/public GraphByMatrix(int size, boolean isDirect) {this.arrayV = new char[size];this.matrix = new int[size][size];this.isDirect = isDirect;for (int i = 0; i < size; i++) {Arrays.fill(matrix[i], Constant.MAX);}}public void initArrayV(char[] array) {for (int i = 0; i < array.length; i++) {this.arrayV[i] = array[i];}}/*** @param srcV 起点* @param destV 终点* @param weight 权值*/public void addEdge(char srcV, char destV, int weight) {int srcIndex = getIndexOfV(srcV);int destIndex = getIndexOfV(destV);matrix[srcIndex][destIndex] = weight;// 如果是无向图,相反的位置也同样需要置为空if (!isDirect) {matrix[destIndex][srcIndex] = weight;}}private int getIndexOfV(char V) {for (int i = 0; i < arrayV.length; i++) {if (arrayV[i] == V) {return i;}}return -1;}/*** 获取顶点的度* 无向图: 行/列 之和* 有向图: 行+列之和** @param V* @return*/public int getDevOfV(char V) {int count = 0;int srcIndex = getIndexOfV(V);for (int i = 0; i < matrix.length; i++) {if (matrix[srcIndex][i] != Constant.MAX) {++count;}}if (isDirect) {for (int i = 0; i < matrix.length; i++) {if (matrix[i][srcIndex] != Constant.MAX) {++count;}}}return count;}public void printGraph() {for (int i = 0; i < arrayV.length; i++) {System.out.print(" " + arrayV[i]);}System.out.println();for (int i = 0; i < matrix.length; i++) {System.out.print(arrayV[i]);for (int j = 0; j < matrix[i].length; j++) {if (matrix[i][j] == Constant.MAX) {System.out.print("∞ ");} else {System.out.print(matrix[i][j] + " ");}}System.out.println();}System.out.println();}
}测试
import Graph.GraphByMatrix;
import Graph.GraphByNode;public class Test {private static void GraphTest() {char[] chars = {'A', 'B', 'C', 'D'};GraphByMatrix graph = new GraphByMatrix(chars.length, false);
// GraphByNode graph = new GraphByNode(chars.length, true);graph.initArrayV(chars);graph.addEdge('A', 'B', 1);graph.addEdge('A', 'D', 1);graph.addEdge('B', 'A', 1);graph.addEdge('B', 'C', 1);graph.addEdge('C', 'B', 1);graph.addEdge('C', 'D', 1);graph.addEdge('D', 'A', 1);graph.addEdge('D', 'C', 1);graph.printGraph();System.out.println(graph.getDevOfV('A'));}public static void main(String[] args) {GraphTest();}
}A B C D
A∞ 1 ∞ 1
B1 ∞ 1 ∞
C∞ 1 ∞ 1
D1 ∞ 1 ∞ 2
邻接表
使用数组存储顶点,链表表示顶点之间的关系【边】
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-64rQYp6r-1666710692075)(../resources/DataStructure/Graph/邻接表.png)]](https://img-blog.csdnimg.cn/383898ee6c5c4ac0abe4d26253188ffa.png)
无向图中同一条边会出现两次,顶点挂载的链表长度就是顶点的度
有向图中一条边只会出现一次,入边表和出边表链表长度之和构成顶点的度
package graph;import java.util.ArrayList;/*
邻接表*/
public class GraphByNode {static class Node {public int src;// 起始位置public int dest;// 目标位置public int weight;// 权重public Node next;public Node(int src, int dest, int weight) {this.src = src;this.dest = dest;this.weight = weight;}}public char[] arrayV;public ArrayList<Node> edgList;// 存储边public boolean isDirect;public GraphByNode(int size, boolean isDirect) {this.arrayV = new char[size];edgList = new ArrayList<>(size);this.isDirect = isDirect;for (int i = 0; i < size; i++) {edgList.add(null);}}/*** 初始化顶点数组** @param array*/public void initArrayV(char[] array) {for (int i = 0; i < array.length; i++) {arrayV[i] = array[i];}}/*** 添加边** @param srcV* @param destV* @param weight*/public void addEdge(char srcV, char destV, int weight) {int srcIndex = getIndexOfV(srcV);int destIndex = getIndexOfV(destV);addEdgeChild(srcIndex, destIndex, weight);if (!isDirect) {addEdgeChild(destIndex, srcIndex, weight);}}private void addEdgeChild(int srcIndex, int destIndex, int weight) {// 这里拿到的是头节点Node cur = edgList.get(srcIndex);while (cur != null) {if (cur.dest == destIndex) {return;}cur = cur.next;}// 之前没有存储过这个边,头插法插入新的边Node node = new Node(srcIndex, destIndex, weight);node.next = edgList.get(srcIndex);edgList.set(srcIndex, node);}private int getIndexOfV(char V) {for (int i = 0; i < arrayV.length; i++) {if (arrayV[i] == V) {return i;}}return -1;}public int getDevOfV(char V) {int count = 0;int srcIndex = getIndexOfV(V);Node cur = edgList.get(srcIndex);while (cur != null) {++count;cur = cur.next;}// 有向图要计算入度if (isDirect) {int destIndex = srcIndex;for (int i = 0; i < edgList.size(); i++) {if (i != destIndex) {Node pCur = edgList.get(i);while (pCur != null) {if (pCur.dest == destIndex) {++count;}pCur = pCur.next;}}}}return count;}public void printGraph() {for (int i = 0; i < edgList.size(); i++) {Node cur = edgList.get(i);System.out.println(arrayV[i] + "_>");while (cur != null) {System.out.print(arrayV[cur.dest] + " ");cur = cur.next;}System.out.println();}System.out.println();}
}测试
import graph.GraphByMatrix;
import graph.GraphByNode;public class Test {private static void GraphTest() {char[] chars = {'A', 'B', 'C', 'D'};
// GraphByMatrix graph = new GraphByMatrix(chars.length, false);GraphByNode graph = new GraphByNode(chars.length, false);graph.initArrayV(chars);graph.addEdge('A', 'B', 1);graph.addEdge('A', 'D', 1);graph.addEdge('B', 'A', 1);graph.addEdge('B', 'C', 1);graph.addEdge('C', 'B', 1);graph.addEdge('C', 'D', 1);graph.addEdge('D', 'A', 1);graph.addEdge('D', 'C', 1);graph.printGraph();System.out.println(graph.getDevOfV('A'));}public static void main(String[] args) {GraphTest();}
}A_>
D B
B_>
C A
C_>
D B
D_>
C A 2
图的遍历
广度优先遍历
回忆一下二叉树的层序遍历代码
private static void levelOrder(BinaryTreeNode root) {if (root == null) {return;} else {Queue<BinaryTreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {BinaryTreeNode top = queue.poll();System.out.print(top.val + " ");if (top.left != null) {queue.offer(top.left);}if (top.right != null) {queue.offer(top.right);}}}
}
对于邻接矩阵,可以模仿二叉树的层序遍历,但是有一个地方改进【会出现最后一个元素的判断错误,如下图所示多打印了一次C】
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qNK7PeFZ-1666710692076)(../resources/DataStructure/Graph/bfs.png)]](https://img-blog.csdnimg.cn/9d260d6231dc4251b389d72996a6480e.png)
public void bfs(char V) {boolean[] visited = new boolean[arrayV.length];int srcIndex = getIndexOfV(V);Queue<Integer> queue = new LinkedList<>();queue.offer(srcIndex);while (!queue.isEmpty()) {int top = queue.poll();visited[top] = true;System.out.print(arrayV[top] + "->");for (int i = 0; i < arrayV.length; i++) {if (matrix[top][i] != Constant.MAX && !visited[i]) {queue.offer(i);// 放进来就置为 true 而不是打印一次置为 true,防止多打印一次visited[i] = true;}}}System.out.println();
}
测试
import graph.GraphByMatrix;
import graph.GraphByNode;public class Test {private static void GraphTest() {char[] chars = {'A', 'B', 'C', 'D'};GraphByMatrix graph = new GraphByMatrix(chars.length, false);
// GraphByNode graph = new GraphByNode(chars.length, false);graph.initArrayV(chars);graph.addEdge('A', 'B', 1);graph.addEdge('A', 'D', 1);graph.addEdge('B', 'A', 1);graph.addEdge('B', 'C', 1);graph.addEdge('C', 'B', 1);graph.addEdge('C', 'D', 1);graph.addEdge('D', 'A', 1);graph.addEdge('D', 'C', 1);
// graph.printGraph();
// System.out.println(graph.getDevOfV('A'));graph.bfs('B');}public static void main(String[] args) {GraphTest();}
}B->A->C->D->
深度优先遍历
和递归类似,与之相关联的一路走到底【类似于二叉树的前序遍历,一条道走到黑】
public void dfs(char V) {boolean[] visited = new boolean[arrayV.length];int srdIndex = getIndexOfV(V);dfsChild(srdIndex, visited);
}private void dfsChild(int srcIndex, boolean[] visited) {System.out.print(arrayV[srcIndex] + "->");visited[srcIndex] = true;for (int i = 0; i < matrix.length; i++) {if (matrix[srcIndex][i] != Constant.MAX && !visited[i]) {dfsChild(i, visited);}}
}
测试
import graph.GraphByMatrix;
import graph.GraphByNode;public class Test {private static void GraphTest() {char[] chars = {'A', 'B', 'C', 'D'};GraphByMatrix graph = new GraphByMatrix(chars.length, false);
// GraphByNode graph = new GraphByNode(chars.length, false);graph.initArrayV(chars);graph.addEdge('A', 'B', 1);graph.addEdge('A', 'D', 1);graph.addEdge('B', 'A', 1);graph.addEdge('B', 'C', 1);graph.addEdge('C', 'B', 1);graph.addEdge('C', 'D', 1);graph.addEdge('D', 'A', 1);graph.addEdge('D', 'C', 1);
// graph.printGraph();
// System.out.println(graph.getDevOfV('A'));
// graph.bfs('B');graph.dfs('B');}public static void main(String[] args) {GraphTest();}
}B->A->D->C->
最小生成树
最小生成树一般用的不多,需要了解一下思想就好了,对代码感兴趣可以查看代码和测试代码<
Kruskal算法
全局找最小
/*** 边*/
class Edge {private int srcIndex;private int destIndex;private int weight;public Edge(int srcIndex, int destIndex, int weight) {this.srcIndex = srcIndex;this.destIndex = destIndex;this.weight = weight;}
}/*** @param minTree 存储找到的边* @return 最小生成树权值和*/
public int kruskal(GraphByMatrix minTree) {PriorityQueue<Edge> minQ = new PriorityQueue<>(new Comparator<Edge>() {@Overridepublic int compare(Edge o1, Edge o2) {return o1.weight - o2.weight;}});// 2.遍历邻接矩阵,存放优先级队列int n = arrayV.length;// 定点个数for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (i < j && matrix[i][j] != Constant.MAX) {minQ.offer(new Edge(i, j, matrix[i][j]));}}}UnionFindSet ufs = new UnionFindSet(n);// 3.开是从优先级队列中取边int size = 0;int totalWeight = 0;while (size < n - 1 && !minQ.isEmpty()) {Edge edge = minQ.poll();int srcIndex = edge.srcIndex;int destIndex = edge.destIndex;if (!ufs.isSameSet(srcIndex, destIndex)) {minTree.addEdgeIndex(srcIndex, destIndex, matrix[srcIndex][destIndex]);System.out.printf("选择的边[%c-%c]:%d\n", arrayV[srcIndex], arrayV[destIndex], matrix[srcIndex][destIndex]);++size;// 记录添加边的条数totalWeight += matrix[srcIndex][destIndex];// 记录最小生成树的权值ufs.union(srcIndex, destIndex);}}if (size == n - 1) {return totalWeight;}return -1;// 没有最小生成树
}private void addEdgeIndex(int srcIndex, int destIndex, int weight) {matrix[srcIndex][destIndex] = weight;if (!isDirect) {matrix[destIndex][srcIndex] = weight;}
}
Prime算法
/**
* @param minTree
* @param V 起点
* @return
*/
public int prime(GraphByMatrix minTree, char V) {
int srcIndex = getIndexOfV(V);
// 存储已经的 X 集合
HashSet<Integer> setX = new HashSet<>();
// 先把确定的定点存入 setX 集合当中
setX.add(srcIndex);
// 存储未初始化的 Y 集合
HashSet<Integer> setY = new HashSet<>();
int n = arrayV.length;
for (int i = 0; i < n; i++) {if (i != srcIndex) {setY.add(i);}
}
// 定一个优先级队列
PriorityQueue<Edge> minQ = new PriorityQueue<>(n, new Comparator<Edge>() {@Overridepublic int compare(Edge o1, Edge o2) {return o1.weight - o2.weight;}
});
// 遍历 srcIndex 链接的所有边
for (int i = 0; i < n; i++) {if (matrix[srcIndex][i] != Constant.MAX) {minQ.offer(new Edge(srcIndex, i, matrix[srcIndex][i]));}
}
// 遍历优先级队列,去除 n-1 条边
int size = 0;
int totalWeight = 0;
while (!minQ.isEmpty()) {Edge edge = minQ.poll();int src = edge.srcIndex;int dest = edge.destIndex;if (setX.contains(dest)) {// 构成环System.out.println("构成环的边[" + arrayV[src] + arrayV[dest] + "]:" + matrix[src][dest]);} else {minTree.addEdgeIndex(src, dest, matrix[src][dest]);System.out.printf("选择的边[%c-%c]:%d\n", arrayV[src], arrayV[dest], matrix[src][dest]);++size;totalWeight += edge.weight;// 更新两个集合setX.add(dest);setY.remove(dest);// 把 dest 链接的边都放入优先队列for (int i = 0; i < n; i++) {if (matrix[dest][i] != Constant.MAX && !setX.contains(i)) {minQ.offer(new Edge(dest, i, matrix[dest][i]));}}}
}
if (size == n - 1) {return totalWeight;
} else {return -1;
}
最短路径
最短路径一般用的不多,需要了解一下思想就好了,对代码感兴趣可以查看代码和测试代码
单源最短——Dijkstra
/*** @param vSrc 指定的起点* @param dist 距离数组* @param pPath 路径*/
public void dijkstra(char vSrc, int[] dist, int[] pPath) {int srcIndex = getIndexOfV(vSrc);// 距离数组初始化Arrays.fill(dist, Constant.MAX);dist[srcIndex] = 0;// 路径数组初始化Arrays.fill(pPath, -1);pPath[srcIndex] = 0;// 当前顶点是否访问过int n = arrayV.length;boolean[] s = new boolean[n];// n 个顶点,要更新 n 次,每次都要从 0 下标开始for (int i = 0; i < n; i++) {int min = Constant.MAX;int u = srcIndex;for (int j = 0; j < n; j++) {if (!s[j] && dist[j] < min) {min = dist[j];u = j;// 更新 u 下标}}s[u] = true;// 松弛链接出去的边for (int j = 0; j < n; j++) {if (!s[j] && matrix[u][j] != Constant.MAX && dist[u] + matrix[u][j] < dist[j]) {dist[j] = dist[u] + matrix[u][j];pPath[j] = u;}}}
}public void printDijkstra(char V, int[] dist, int[] pPath) {int srcIndex = getIndexOfV(V);int n = arrayV.length;for (int i = 0; i < n; i++) {if (i != srcIndex) {ArrayList<Integer> path = new ArrayList<>();int parent = i;while (parent != srcIndex) {path.add(parent);parent = pPath[parent];}path.add(srcIndex);Collections.reverse(path);for (int pos : path) {System.out.print(arrayV[pos] + "->");}System.out.println(dist[i]);}}
}
单源最短——Bellman-Ford
public boolean bellmanFord(char V, int[] dist, int[] pPath) {int srcIndex = getIndexOfV(V);// 距离数组初始化Arrays.fill(dist, Constant.MAX);dist[srcIndex] = 0;// 路径数组初始化Arrays.fill(pPath, -1);pPath[srcIndex] = 0;int n = arrayV.length;for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] != Constant.MAX && dist[i] + matrix[i][j] < dist[j]) {dist[j] = dist[i] + matrix[i][j];pPath[j] = i;}}}}// 判断是否存在负权回路【顶点 a 到 顶点b 路径值为负】for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] != Constant.MAX && dist[i] + matrix[i][j] < dist[j]) {return false;}}}return true;
}
多源最短——Floyd-Warshall
public void floydWarShall(int[][] dist, int[][] pPath) {int n = arrayV.length;for (int i = 0; i < n; i++) {Arrays.fill(dist[i], Constant.MAX);Arrays.fill(pPath[i], -1);}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] != Constant.MAX) {dist[i][j] = matrix[i][j];pPath[i][j] = i;} else {pPath[i][j] = -1;}if (i == j) {dist[i][j] = 0;pPath[i][j] = -1;}}}for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (dist[i][k] != Constant.MAX && dist[k][j] != Constant.MAX && dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];// 更新父节点下标// pPath[i][j] = k;//不对// 如果 i->k k->j 此时是对的;但是如果中间经历了很多节点 i->x->...k->s->...->jpPath[i][j] = pPath[k][j];}}}}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (dist[i][j] == Constant.MAX) {System.out.print(" * ");} else {System.out.print(dist[i][j] + " ");}}System.out.println();}System.out.println("=========打印路径==========");for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.print(pPath[i][j] + " ");}System.out.println();}System.out.println("==========================");
}
测试
import graph.GraphByMatrix;public class Test {private static void GraphTest() {char[] chars = {'A', 'B', 'C', 'D'};GraphByMatrix graph = new GraphByMatrix(chars.length, false);
// GraphByNode graph = new GraphByNode(chars.length, false);graph.initArrayV(chars);graph.addEdge('A', 'B', 1);graph.addEdge('A', 'D', 1);graph.addEdge('B', 'A', 1);graph.addEdge('B', 'C', 1);graph.addEdge('C', 'B', 1);graph.addEdge('C', 'D', 1);graph.addEdge('D', 'A', 1);graph.addEdge('D', 'C', 1);
// graph.printGraph();
// System.out.println(graph.getDevOfV('A'));
// graph.bfs('B');
// graph.dfs('B');String str = "abcdefghi";char[] array = str.toCharArray();GraphByMatrix g = new GraphByMatrix(str.length(), false);g.initArrayV(array);g.addEdge('a', 'b', 4);g.addEdge('a', 'h', 8);
// g.addEdge('a', 'h', 9);g.addEdge('b', 'c', 8);g.addEdge('b', 'h', 11);g.addEdge('c', 'i', 2);g.addEdge('c', 'f', 4);g.addEdge('c', 'd', 7);g.addEdge('d', 'f', 14);g.addEdge('d', 'e', 9);g.addEdge('e', 'f', 10);g.addEdge('f', 'g', 2);g.addEdge('g', 'h', 1);g.addEdge('g', 'i', 6);g.addEdge('h', 'i', 7);GraphByMatrix kminTree = new GraphByMatrix(str.length(), false);System.out.println(g.kruskal(kminTree));kminTree.printGraph();str = "abcdefghi";array = str.toCharArray();g = new GraphByMatrix(str.length(), false);g.initArrayV(array);g.addEdge('a', 'b', 4);g.addEdge('a', 'h', 8);
// g.addEdge('a', 'h', 9);g.addEdge('b', 'c', 8);g.addEdge('b', 'h', 11);g.addEdge('c', 'i', 2);g.addEdge('c', 'f', 4);g.addEdge('c', 'd', 7);g.addEdge('d', 'f', 14);g.addEdge('d', 'e', 9);g.addEdge('e', 'f', 10);g.addEdge('f', 'g', 2);g.addEdge('g', 'h', 1);g.addEdge('g', 'i', 6);g.addEdge('h', 'i', 7);GraphByMatrix primTree = new GraphByMatrix(str.length(), false);System.out.println(g.prime(primTree, 'a'));primTree.printGraph();str = "syztx";array = str.toCharArray();g = new GraphByMatrix(array.length, true);g.initArrayV(array);g.addEdge('s', 't', 10);g.addEdge('s', 'y', 5);g.addEdge('y', 't', 3);g.addEdge('y', 'x', 9);g.addEdge('y', 'z', 2);g.addEdge('z', 's', 7);g.addEdge('z', 'x', 6);g.addEdge('t', 'y', 2);g.addEdge('t', 'x', 1);g.addEdge('x', 'z', 4);int[] dist = new int[array.length];int[] pPath = new int[array.length];g.dijkstra('s', dist, pPath);g.printDijkstra('s', dist, pPath);str = "syztx";array = str.toCharArray();g = new GraphByMatrix(array.length, true);g.initArrayV(array);g.addEdge('s', 't', 6);g.addEdge('s', 'y', 7);g.addEdge('y', 'z', 9);g.addEdge('y', 'x', -3);g.addEdge('z', 's', 2);g.addEdge('z', 'x', 7);g.addEdge('t', 'x', 5);g.addEdge('t', 'y', 8);g.addEdge('t', 'z', -4);g.addEdge('x', 't', -2);//负权回路实例/*g.addEdge('s', 't', 6);g.addEdge('s', 'y', 7);g.addEdge('y', 'z', 9);g.addEdge('y', 'x', -3);g.addEdge('y', 's', 1);g.addEdge('z', 's', 2);g.addEdge('z', 'x', 7);g.addEdge('t', 'x', 5);g.addEdge('t', 'y', -8);g.addEdge('t', 'z', -4);g.addEdge('x', 't', -2);*/dist = new int[array.length];pPath = new int[array.length];boolean flg = g.bellmanFord('s', dist, pPath);if (flg) {g.printDijkstra('s', dist, pPath);} else {System.out.println("存在负权回路");}str = "12345";array = str.toCharArray();g = new GraphByMatrix(array.length, true);g.initArrayV(array);g.addEdge('1', '2', 3);g.addEdge('1', '3', 8);g.addEdge('1', '5', -4);g.addEdge('2', '4', 1);g.addEdge('2', '5', 7);g.addEdge('3', '2', 4);g.addEdge('4', '1', 2);g.addEdge('4', '3', -5);g.addEdge('5', '4', 6);int[][] d_dist = new int[array.length][array.length];int[][] p_path = new int[array.length][array.length];g.floydWarShall(d_dist, p_path);for (int i = 0; i < array.length; i++) {g.printDijkstra(array[i], d_dist[i], p_path[i]);System.out.println("*************************");}}public static void main(String[] args) throws NoSuchFieldException, IllegalAccessException {GraphTest();}
}选择的边[g-h]:1
选择的边[f-g]:2
选择的边[c-i]:2
选择的边[a-b]:4
选择的边[c-f]:4
选择的边[c-d]:7
选择的边[b-c]:8
选择的边[d-e]:9
37∞ 4 ∞ ∞ ∞ ∞ ∞ ∞ ∞
4 ∞ 8 ∞ ∞ ∞ ∞ ∞ ∞
∞ 8 ∞ 7 ∞ 4 ∞ ∞ 2
∞ ∞ 7 ∞ 9 ∞ ∞ ∞ ∞
∞ ∞ ∞ 9 ∞ ∞ ∞ ∞ ∞
∞ ∞ 4 ∞ ∞ ∞ 2 ∞ ∞
∞ ∞ ∞ ∞ ∞ 2 ∞ 1 ∞
∞ ∞ ∞ ∞ ∞ ∞ 1 ∞ ∞
∞ ∞ 2 ∞ ∞ ∞ ∞ ∞ ∞ 选择的边[a-b]:4
选择的边[a-h]:8
选择的边[h-g]:1
选择的边[g-f]:2
选择的边[f-c]:4
选择的边[c-i]:2
构成环的边[gi]:6
构成环的边[hi]:7
选择的边[c-d]:7
构成环的边[bc]:8
选择的边[d-e]:9
构成环的边[fe]:10
构成环的边[bh]:11
构成环的边[fd]:14
37∞ 4 ∞ ∞ ∞ ∞ ∞ 8 ∞
4 ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
∞ ∞ ∞ 7 ∞ 4 ∞ ∞ 2
∞ ∞ 7 ∞ 9 ∞ ∞ ∞ ∞
∞ ∞ ∞ 9 ∞ ∞ ∞ ∞ ∞
∞ ∞ 4 ∞ ∞ ∞ 2 ∞ ∞
∞ ∞ ∞ ∞ ∞ 2 ∞ 1 ∞
8 ∞ ∞ ∞ ∞ ∞ 1 ∞ ∞
∞ ∞ 2 ∞ ∞ ∞ ∞ ∞ ∞ s->y->5
s->y->z->7
s->y->t->8
s->y->t->x->9
s->y->7
s->y->x->t->z->-2
s->y->x->t->2
s->y->x->4
0 1 -3 2 -4
3 0 -4 1 -1
7 4 0 5 3
2 -1 -5 0 -2
8 5 1 6 0
=========打印路径==========
-1 2 3 4 0
3 -1 3 1 0
3 2 -1 1 0
3 2 3 -1 0
3 2 3 4 -1
==========================
1->5->4->3->2->1
1->5->4->3->-3
1->5->4->2
1->5->-4
*************************
2->4->1->3
2->4->3->-4
2->4->1
2->4->1->5->-1
*************************
3->2->4->1->7
3->2->4
3->2->4->5
3->2->4->1->5->3
*************************
4->1->2
4->3->2->-1
4->3->-5
4->1->5->-2
*************************
5->4->1->8
5->4->3->2->5
5->4->3->1
5->4->6
*************************
其它高阶算法总结
剩下部分的高阶算法查找需要耐心查看学习,不是一日而成的。高阶数据结构中红黑树并不是万能的,也不是某一个数据结构能够屡试不爽的,经常有同学问我是不是红黑树查找效率最高需要结合业务场景进行具体使用。