Windows操作系统自带时间同步功能，它会自动从互联网时间服务器获取时间，以保证系统时间的准确性。但是，有时候我们需要更改时间服务器，以获得更准确的时间同步。小编将为大家介绍如何更改Windows时间服务器，以及Windows时间服务器的配置方法。

　　一、更改Windows时间服务器的方法

　　在更改Windows时间服务器之前，需要先了解当前系统使用的时间服务器。您可以通过以下方法检查当前系统使用的时间服务器：

　　1. 使用命令行

　　按下Win+R键打开运行窗口，输入cmd并回车，打开命令行窗口。输入以下命令并回车：

　　w32tm /query /peers

　　该命令会显示当前系统使用的时间服务器。

　　2. 使用系统设置

　　单击任务栏上的时间显示，选择“日期和时间设置”，然后单击“更改日期和时间设置”。

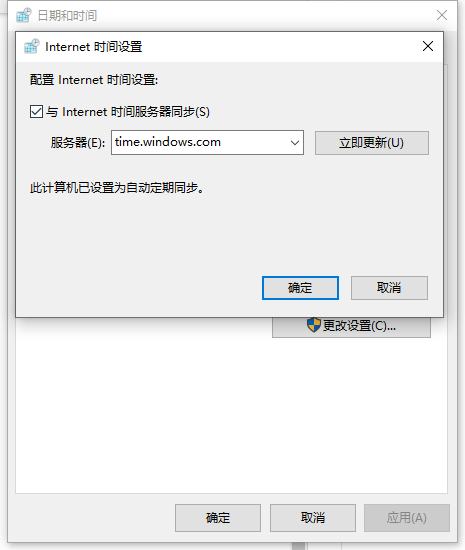
　　在弹出的窗口中，选择“Internet时间”选项卡，然后单击“更改设置”按钮。

　　在弹出的窗口中，您可以查看当前系统使用的时间服务器。

　　要更改Windows时间服务器，您可以按照以下步骤进行：

　　1. 打开命令行窗口，输入以下命令并回车：

　　w32tm /config /manualpeerlist:时间服务器IP地址 /syncfromflags:manual /reliable:yes /update

　　其中，“时间服务器IP地址”为您想要使用的时间服务器的IP地址。例如，您可以使用国家授时中心的时间服务器，其IP地址为time.nist.gov。

　　2. 输入以下命令并回车：

　　net stop w32time

　　net start w32time

　　这将重新启动Windows时间服务。

　　二、Windows时间服务器的配置方法

　　除了更改Windows时间服务器外，您还可以对Windows时间服务器进行配置，以获得更准确的时间同步效果。以下是Windows时间服务器的配置方法：

　　1. 打开命令行窗口，输入以下命令并回车：

　　w32tm /config /manualpeerlist:时间服务器IP地址 /syncfromflags:manual /reliable:yes /update

　　其中，“时间服务器IP地址”为您想要使用的时间服务器的IP地址。例如，您可以使用国家授时中心的时间服务器，其IP地址为time.nist.gov。

　　2. 输入以下命令并回车：

　　w32tm /config /update

　　net stop w32time

　　net start w32time

这将重新启动Windows时间服务，并更新配置。

　　3. 检查Windows时间服务器配置是否成功。输入以下命令并回车：

　　w32tm /query /configuration

　　该命令会显示当前Windows时间服务器的配置信息。

　　Windows时间同步功能可以保证系统时间的准确性，但有时候需要更改时间服务器以获得更精确的时间同步效果。本文介绍了如何更改Windows时间服务器以及Windows时间服务器的配置方法。如果您发现您的系统时间不准确，可以按照本文所述方法进行更改和配置。