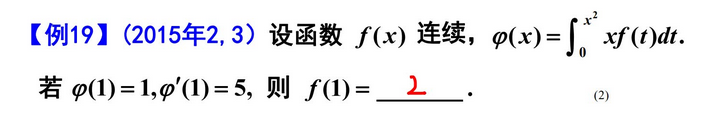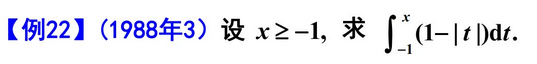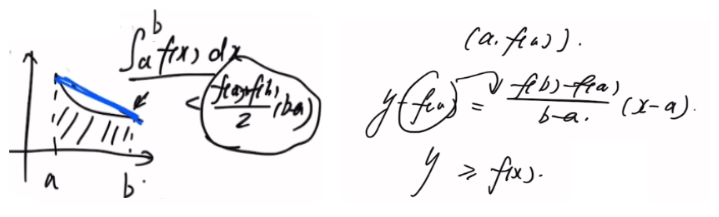一、定积分的概念、性质及几何意义
巧解：利用奇偶性，快速选出答案。
利用图形帮助解题。
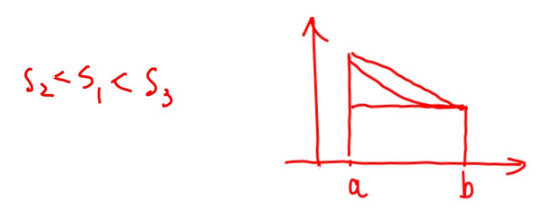
设出具体函数。
二、定积分的计算
1.利用几何意义
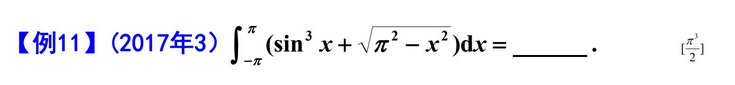
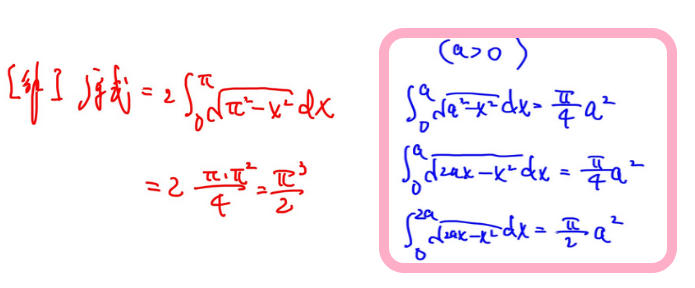
2.换元法巧解
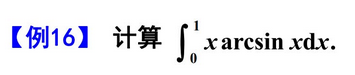
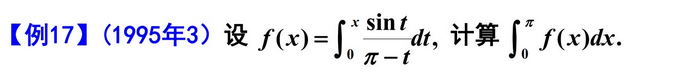
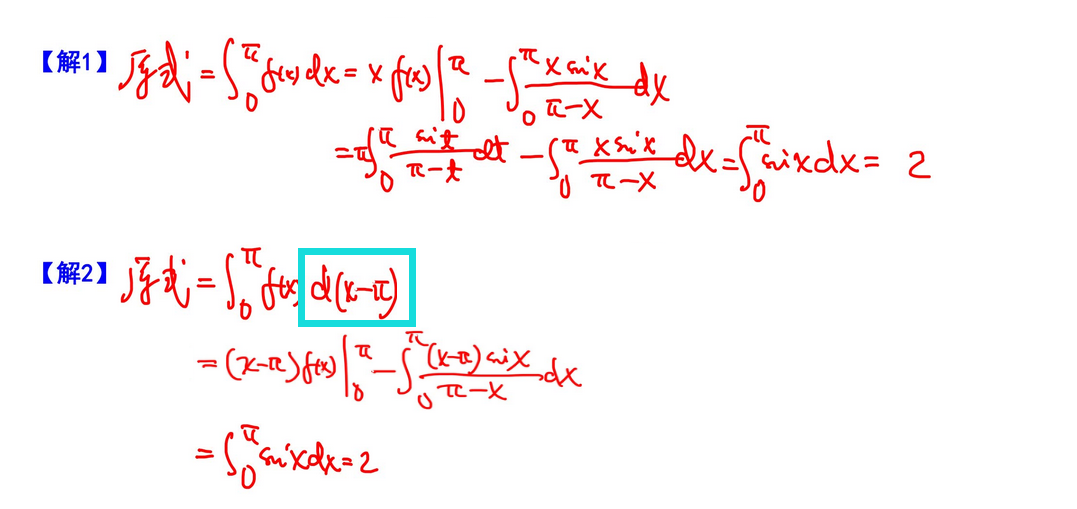
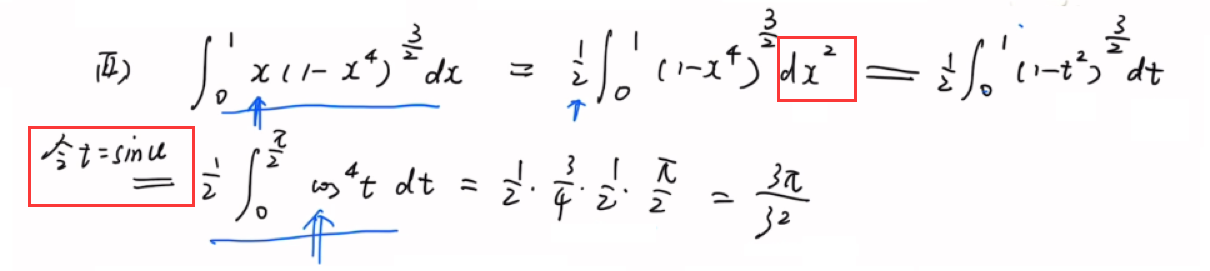
3.区间平移
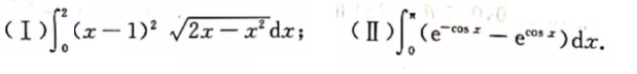
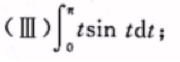
本题也可用用区间再现
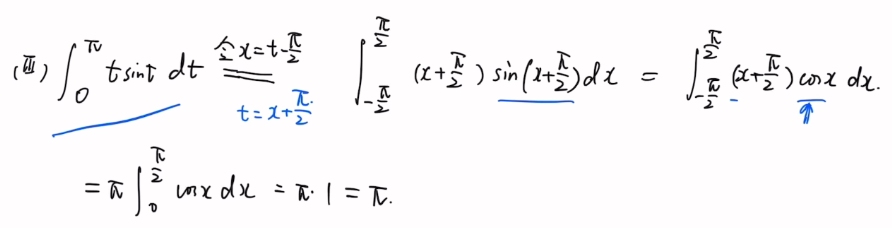
4.绝对值符号讨论
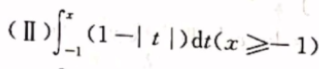
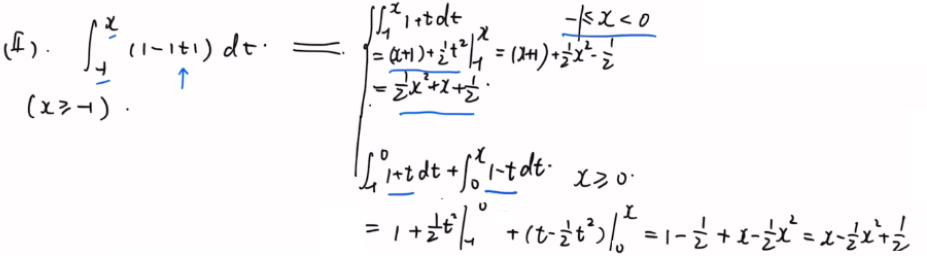
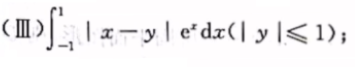
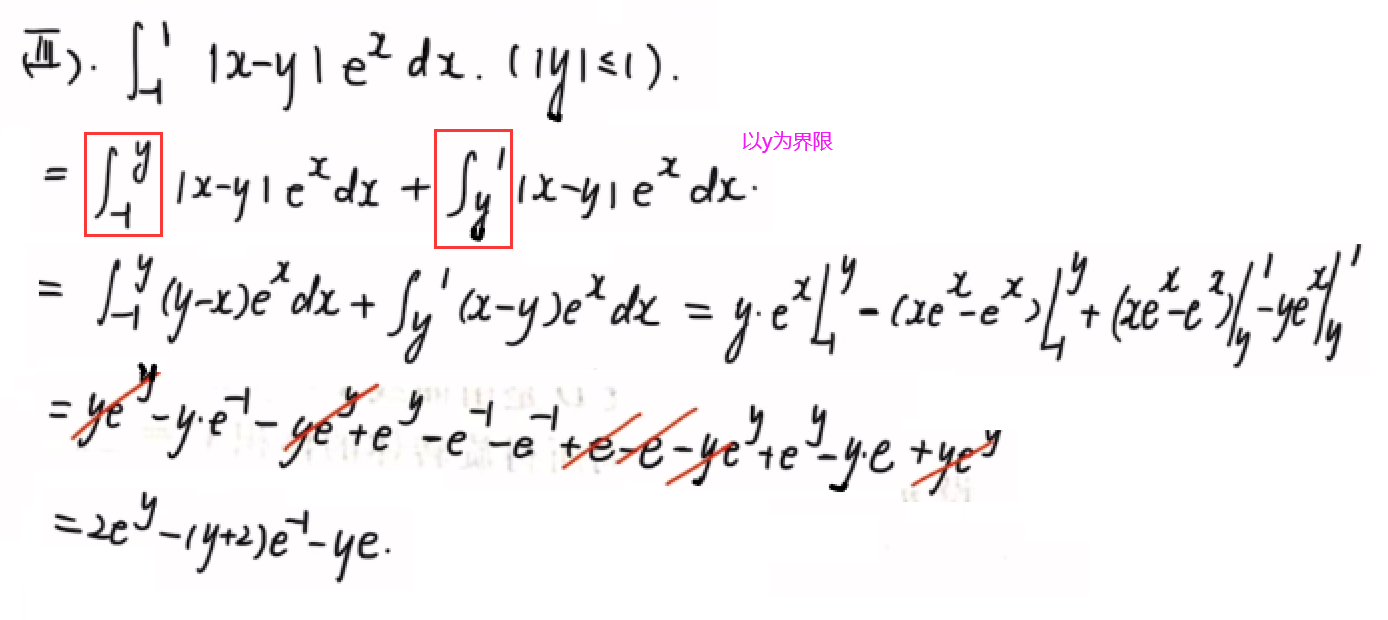
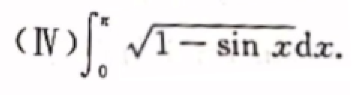
三、变上限定积分
三种变限积分形式
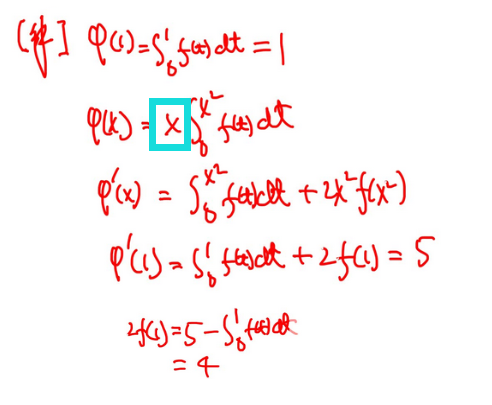
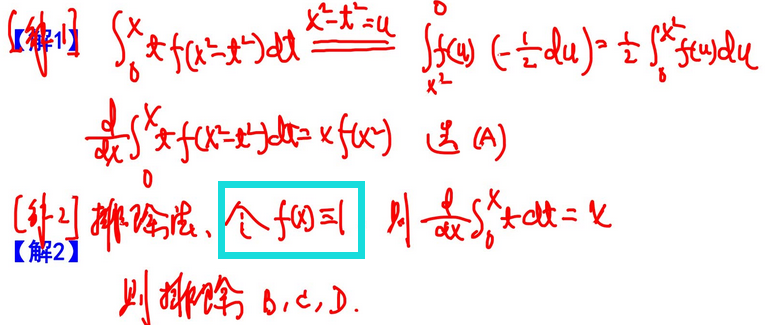
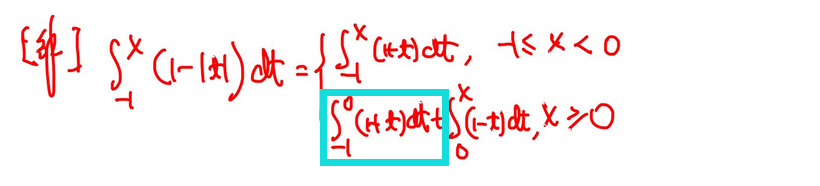
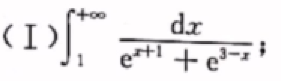
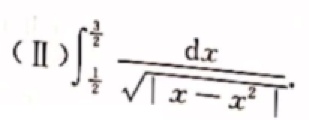
四、李林 相关证明题及综合题
1. 证明题
一般遇到二阶导，可以考虑
①泰勒展开。
②两次拉格朗日
遇到定积分形式不等式，一般考虑把其中一个字母推广为x。
使用积分中值定理时，如果不知道该取开还是闭，一般取开区间。
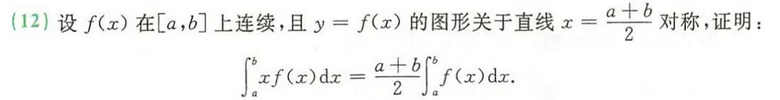
区间再现！+ 恒等变形
妙啊！！
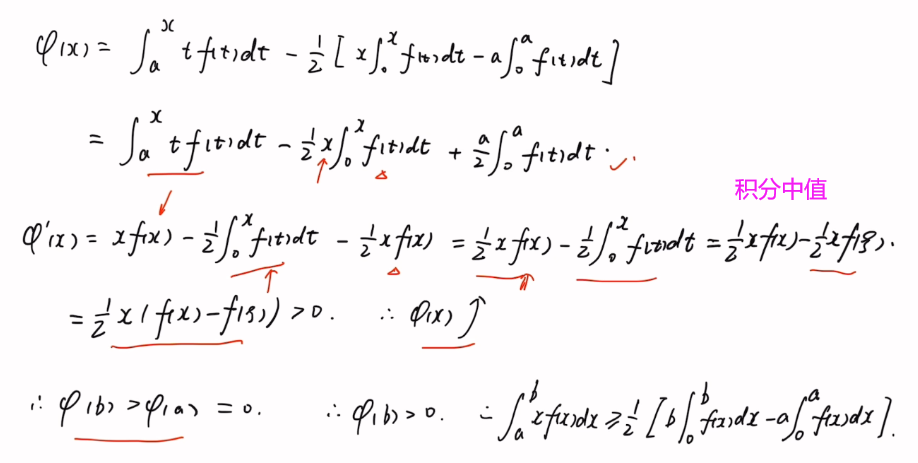
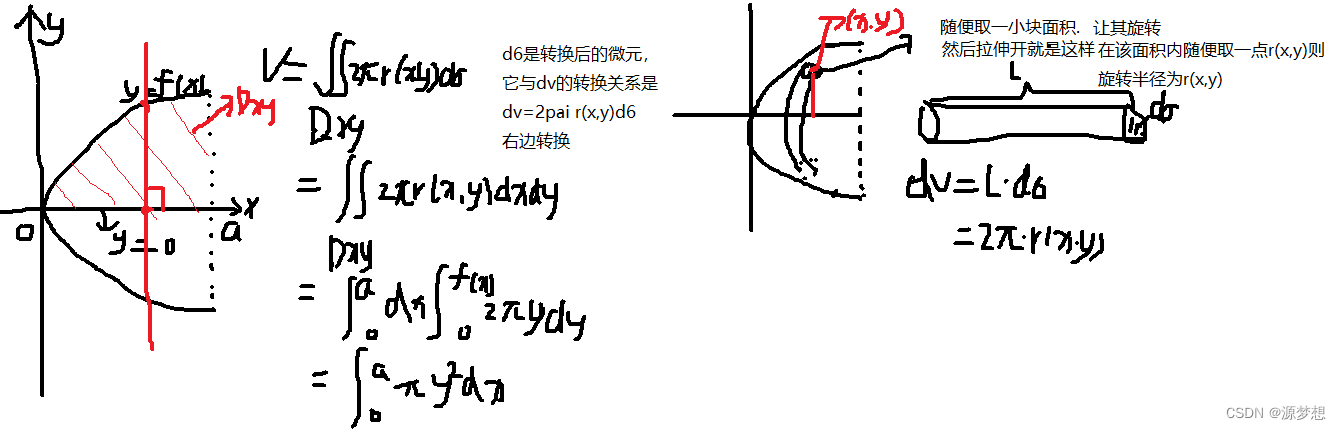
2. 基础解答题
参数方程、上下限
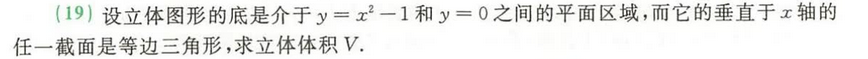
微元法、dv = 截面面积 ds
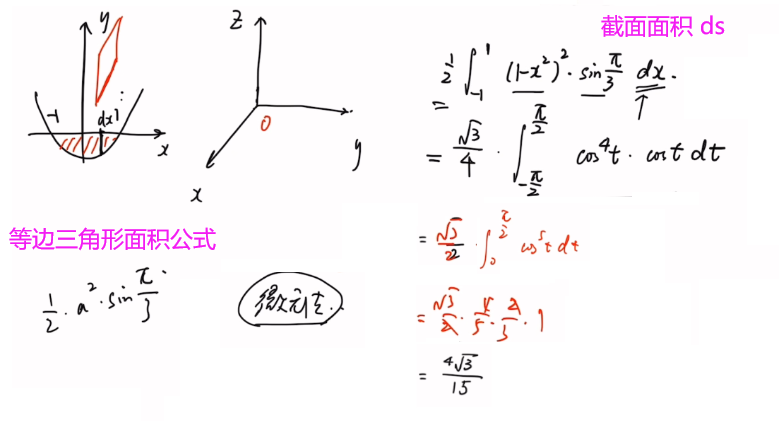
3. 综合选择题
定积分的化简问题：
- ①换元：区间再现 x=a+b-t
- ②区间平移：奇偶性
- ③拆分：积分区间可加性
解：拆分，因sint在两个区间正负不同。
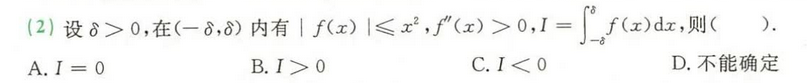
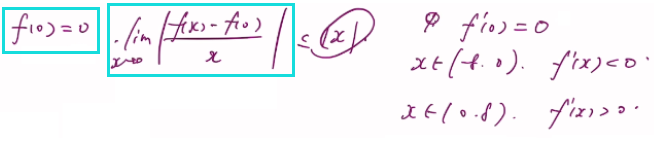
解：利用拉格朗日反写 f（x）。
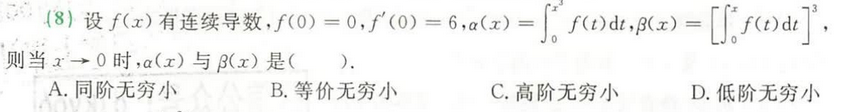
无穷小比较：
- ①用定义，求极限之比
- ②挨个看，他与x的几阶是同阶的
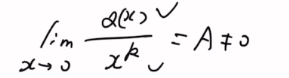因为分子是变限积分函数，所以求极限一定会洛必达。
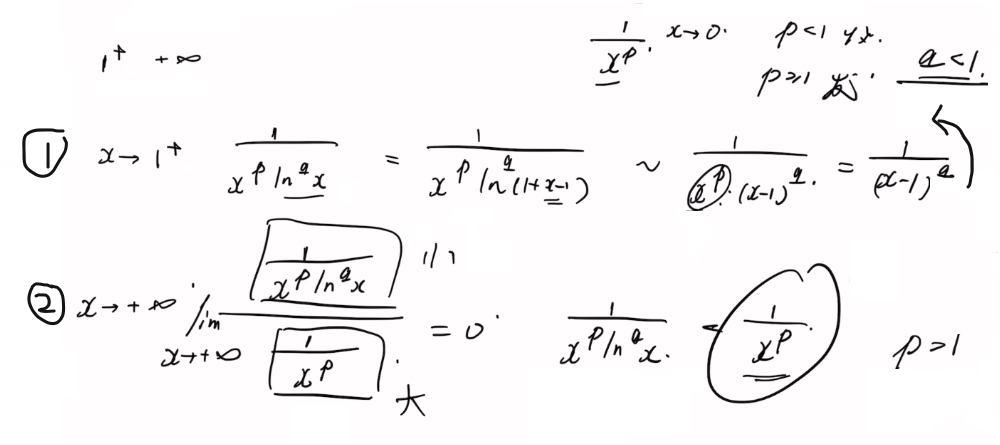
反常积分首先看瑕点。
4. 综合填空题
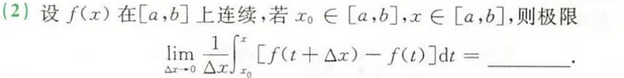
两个解法：设出F（x）
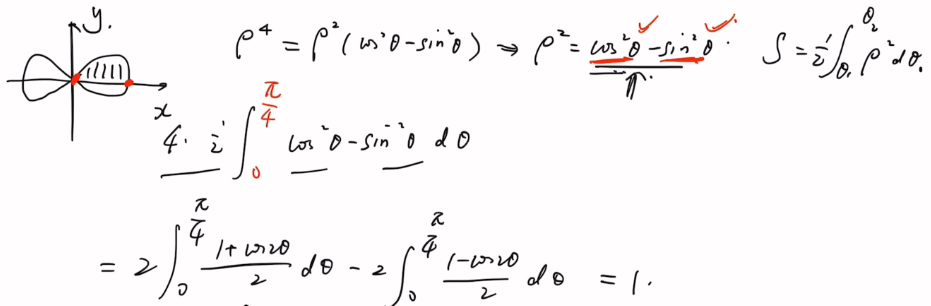
5. 综合解答题
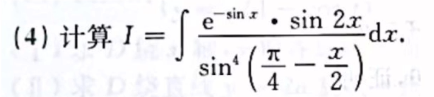
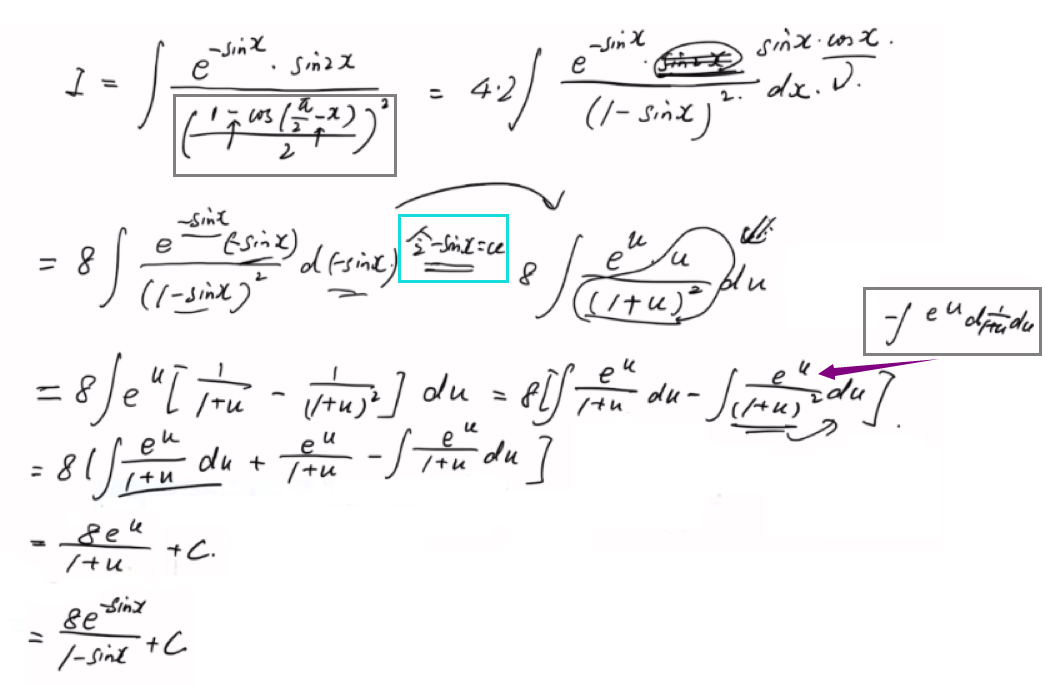
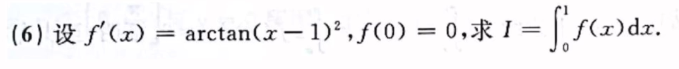
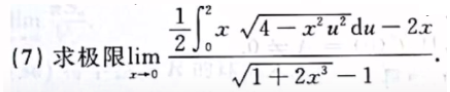
凑整体！
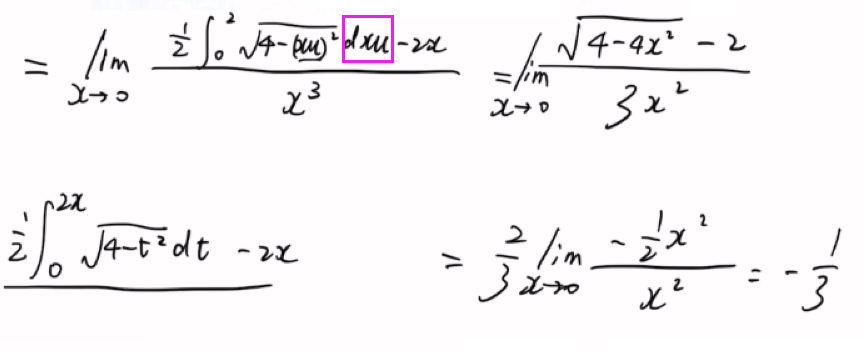
凑整体！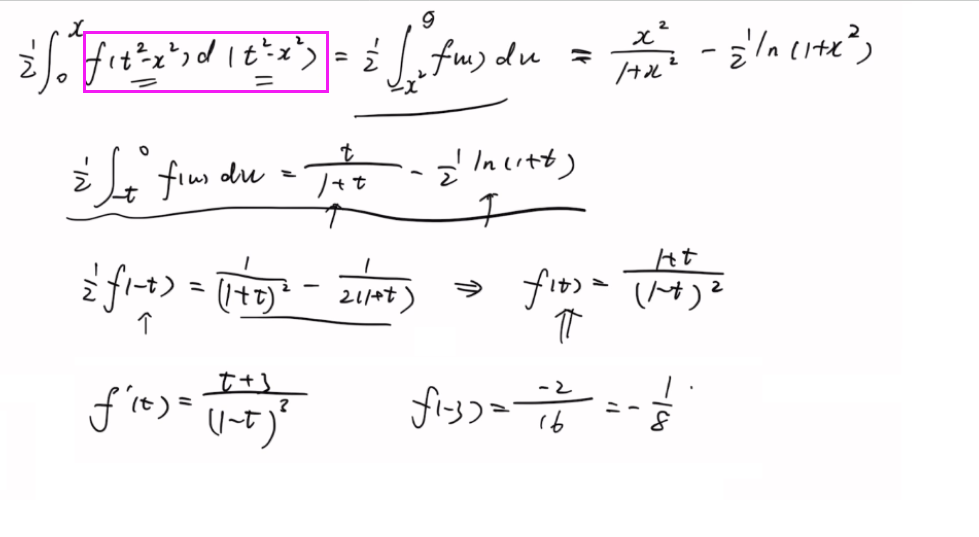
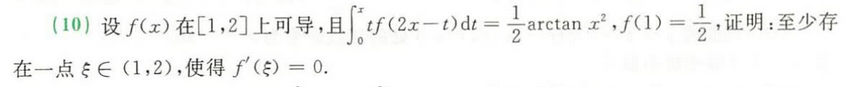
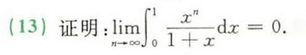
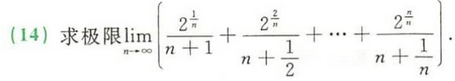
夹逼准则放缩过渡一下~再利用定积分定义！
如果最大的分母和最小的分母作商取极限的结果为1，则可以放缩~~~~
如果作商结果为1，意味着分母之间差距很小。
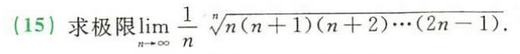
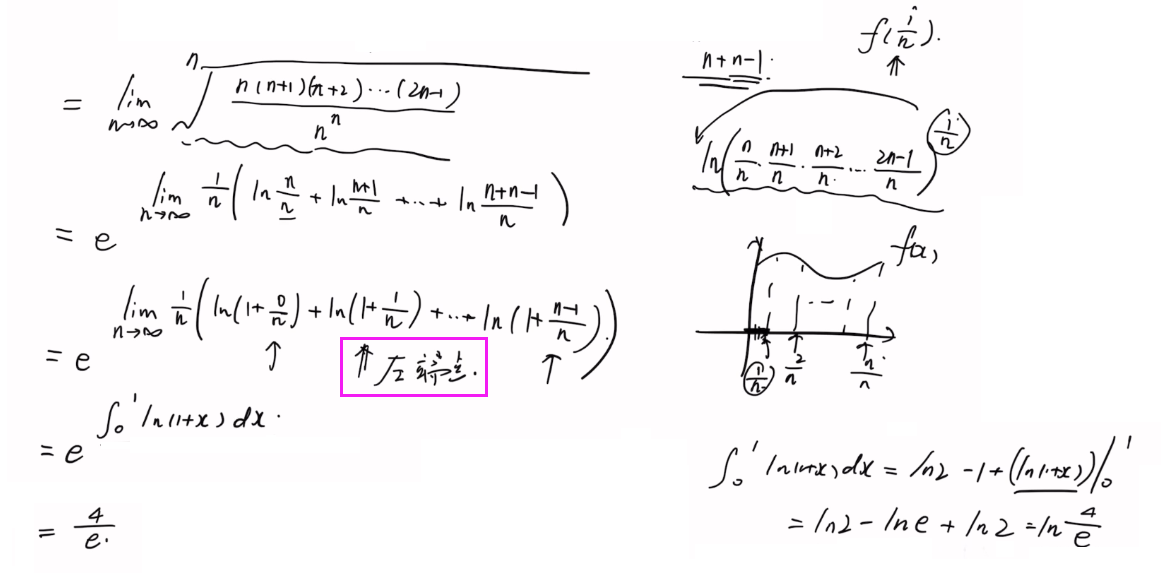
· 递推关系
递归：用分部积分！！
不等式利用单调性！！
妙！！！！
或者 三角函数转化成一个幂函数
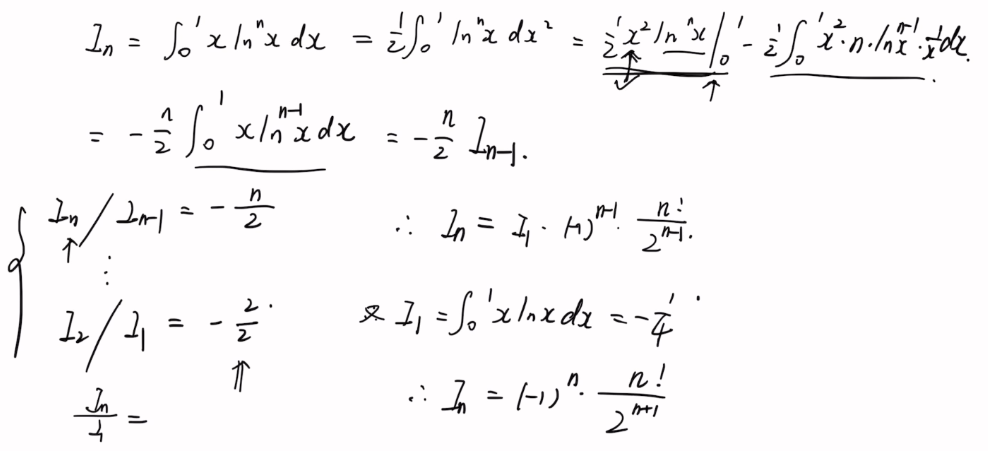
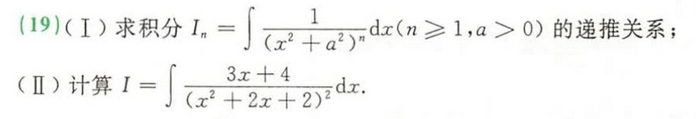
· 证明类
类似同济教材 拉格朗日中值定理的证明 用曲线减直线 构造直线方程。
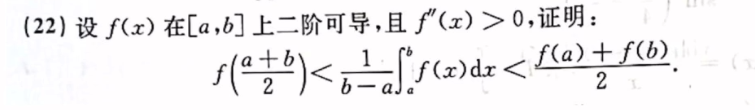
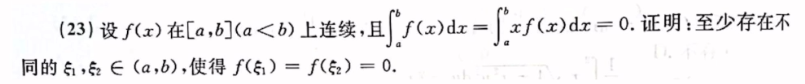
找到原函数，中三个函数点，两两罗尔。
抽象函数：积分中值定理或分部
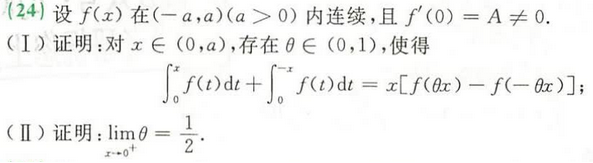
拉格朗日中值定理的特殊形式
凑导数定义
零点定理失效，退而求其次。
构造辅助函数，利用罗尔定理。
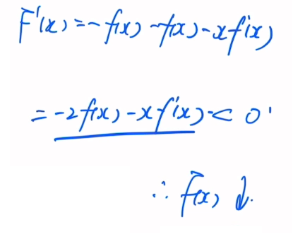
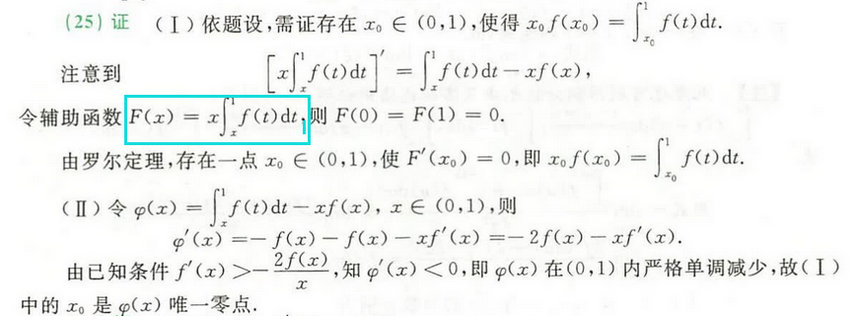
第一问。基本上都是要换元。
相反数换元 令x=—u。周期换元 令x=u+T。但是第一问不好操作。
本题应该使用区间再现。区间没变首先想到区间再现。
法一：假设F（x）
类似上文综合填空题第一个。题目在李林2023 880 p20 第2个填空。
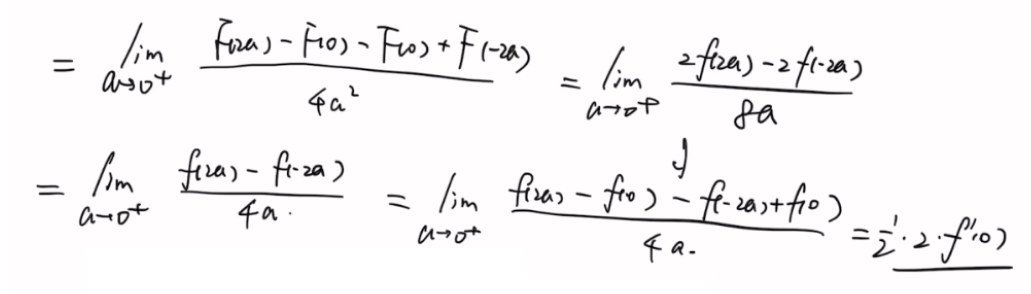
法二：积分中值定理
法三：积分换元 + 洛必达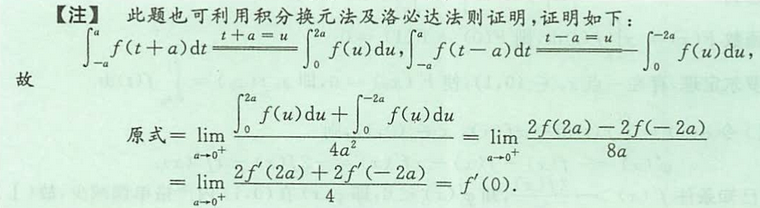 
· 应用类
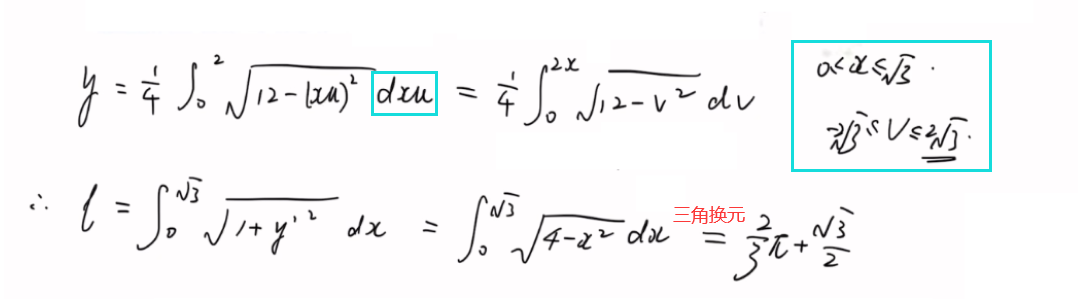
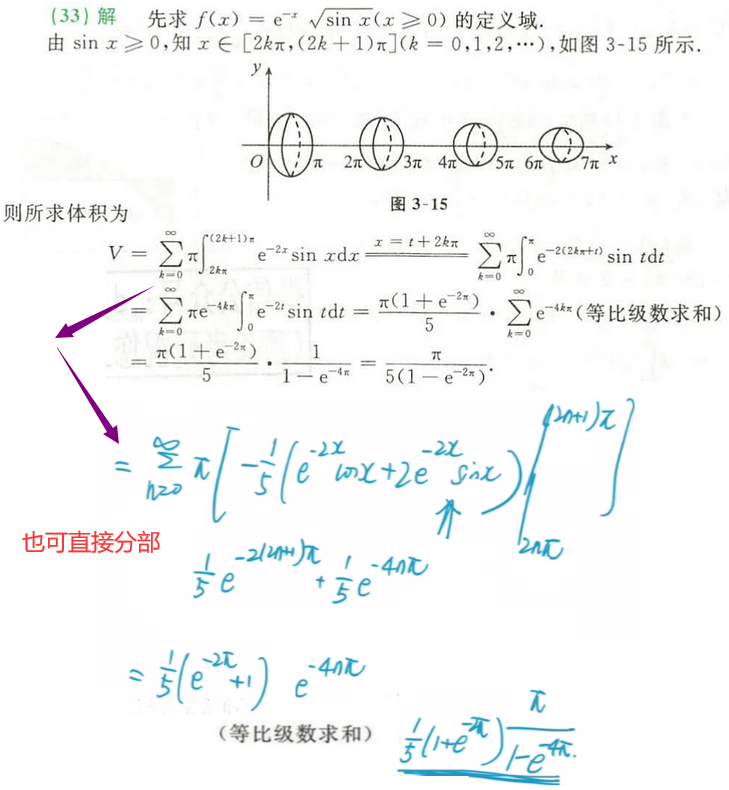
三种积分方法。
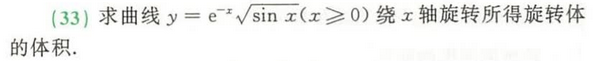
无穷个体积。之前考研出现过 e^-x sinx 的面积
