编译环境：ubuntu17.04 Python3.5

所需库：numpy、scipy、matplotlib

下面是理想平面的辐射强度计算(课程大作业～～～)

1、超越函数积分运算

def integral(x,c1,c2,T):

return ((c1*0.98)/(x**5))*(1/((np.e**(c2/(x*T)))-1))

resut,err = integrate.quad(integral, 3, 5, args=(c1,c2,T))

2、绘图实现

plt.figure(1)

ax1 = plt.subplot(211)

plt.sca(ax1)

plt.plot(fi,functionI(fi,0.5,5,1,e0),label='n=5,ks=0.5')

plt.legend(loc='upper right',bbox_to_anchor = (0.9, 0.9))

plt.xlabel(u'ψ/rad')

plt.ylabel(u'I/(W/sr)')

ax2 = plt.subplot(212)

plt.sca(ax2)

plt.plot(fi,functionI(fi,0.5,5,1,e0),label='n=5,ks=0.5')

plt.legend(loc='upper right',bbox_to_anchor = (0.9, 0.9))

plt.xlabel(u'ψ/rad')

plt.ylabel(u'I/(W/sr)')

plt.subplots_adjust(wspace=0.5, hspace=0.5)

plt.show()

说一下plt.subplots_adjust这个函数，这个是用来调整子图之间的间距的啦

成果图：

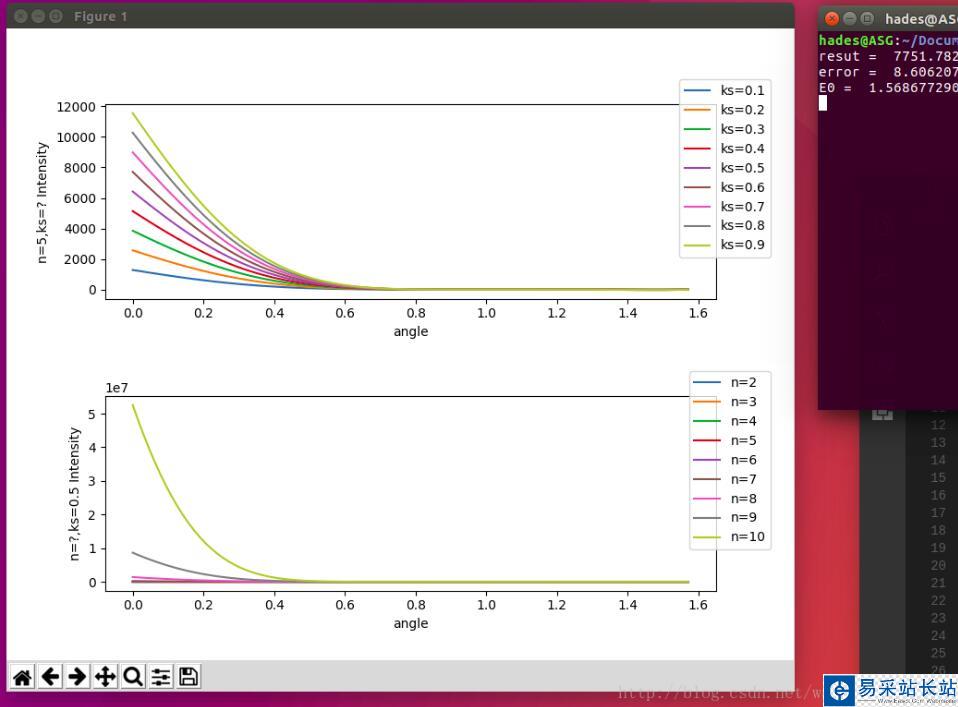
以上这篇Python超越函数积分运算以及绘图实现代码就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持易采站长站。