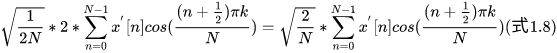原创: Lebhoryi@rt-thread.com
时间: 2020/05/11
结合 tf2 官网mfcc例程阅读本篇文档食用更佳
rfft 部分没有吃透，未来待补
Update: 新增tensorflow2 调用tf1的API 实现mfcc提取；
Update: 新增全文代码下载链接
Date: 2020/07/27

文章目录

0x00 前言概述
0x01 读取语音源文件
0x02 填充及分帧 & 加窗 & 快速傅里叶变换
- 2.1 分帧 & 填充
- 2.2 加窗
- 2.3 傅里叶变换
- 2.4 对spectrum 取绝对值 & 平方
0x03 梅尔滤波
- 3.1 构造梅尔滤波器组（每一帧抽取40个特征）
- 3.2 计算梅尔滤波器的参数
- - 3.2.1 转换
  - 3.2.2 均等划分
  - 3.2.3 分帧，分出前中后三个滤波器参数
  - 3.2.4 建立滤波器
- 3.3 矩阵乘法
0x04 进行log变换
0x05 采用DCT得到MFCC
0x06 参考文献

0x00 前言概述

###################################

update 2020/08/10
tf2 实现mfcc 代码下载 ☞ 传送门

###################################

update 2020/07/27

tensorflow2 调用 tensorflow1 的API 实现mfcc 提取, 贼简单, 不需要了解太多关于mfcc的细节,
如果要对mfcc 内部进行一个了解, 请深入下文详细阅读

import tensorflow as tf
from tensorflow.python.ops import gen_audio_ops as audio_ops
from tensorflow.python.ops import io_opsdef get_mfcc_simplify(wav_filename, desired_samples,window_size_samples, window_stride_samples):wav_loader = io_ops.read_file(wav_filename)wav_decoder = contrib_audio.decode_wav(wav_loader, desired_channels=1, desired_samples=desired_samples)# Run the spectrogram and MFCC ops to get a 2D 'fingerprint' of the audio.spectrogram = contrib_audio.audio_spectrogram(wav_decoder.audio,window_size=window_size_samples,stride=window_stride_samples,magnitude_squared=True)mfcc_ = contrib_audio.mfcc(spectrogram,wav_decoder.sample_rate,dct_coefficient_count=dct_coefficient_count)return mfcc_if __name__ == "__main__":sample_rate, window_size_ms, window_stride_ms = 16000, 40, 20dct_coefficient_count = 30clip_duration_ms = 1000desired_samples = int(sample_rate * clip_duration_ms / 1000)window_size_samples = int(sample_rate * window_size_ms / 1000)window_stride_samples = int(sample_rate * window_stride_ms / 1000)_mfcc = get_mfcc_simplify("../../data/xrxr/1.wav", desired_samples,window_size_samples, window_stride_samples)print(_mfcc)

Q: 为什么搞tensorflow2实现mfcc提取？网上不是有一大把教程和python自带两个库的实现的吗？
A: 想学习mfcc是如何计算获得，并用代码实现（该项目是tensorflow提供的语音唤醒例子下）
在tensorflow1.14及之前的版本中，它是这么实现的：
```
# stft , get spectrogram
spectrogram = contrib_audio.audio_spectrogram(wav_decoder.audio,window_size=640,stride=640,magnitude_squared=True)# get mfcc (C, H, W)
_mfcc = contrib_audio.mfcc(spectrogram,sample_rate=16000,upper_frequency_limit=4000,lower_frequency_limit=20,filterbank_channel_count=40,dct_coefficient_count=10)
```
只能获取到中间语谱图(spectrogram)变量, 而当我想要获取mfcc计算过程中的加窗、梅尔滤波器等的相关信息，是极难获取的，需要很强的代码功底，它内部实现的代码传送门：gen_audio_ops.py

好吧，我第一次被代码劝退了。

他山之石可以攻玉，转而看一下其他获取mfcc的方式（脚本），网上有教程说是python自带的两个库可以实现mfcc获取:

librosa && python_speech_feature

但是遇到很棘手的一个问题：
- mfcc值和tensorflow1.14计算的值并不相同啊
如此之后，偶有看到tensorflow 2.1.0的mfccs_from_log_mel_spectrograms可以分步骤的计算mfcc，修修改改，最终得到了现在这个版本

以下代码均在tensorflow2.1.0 版本下执行

基本流程：语音读取 --> 预加重（本文无预加重） --> 分帧 --> 加窗 --> FFT -->Mel滤波器组 -->对数运算 --> DCT

0x01 读取语音源文件

shape = wav.length

import tensorflow as tf
import numpy as np
from tensorflow.python.ops import io_ops
from tensorflow import audiodef load_wav(wav_path, sample_rate=16000):'''load one wav fileArgs:wav_path: the wav file path, strsample_rate: wav's sample rate, int8Returns:wav: wav文件信息, 有经过归一化操作, float32rate: wav's sample rate, int8'''wav_loader = io_ops.read_file(wav_path)(wav, rate) = audio.decode_wav(wav_loader,desired_channels=1,desired_samples=sample_rate)# shape (16000,)wav = np.array(wav).flatten()return wav, rate

0x02 填充及分帧 & 加窗 & 快速傅里叶变换

input shape: wav, shape = wav.shape

output : spectrograms without padding, shape = (n_frames, num_spectrogram_bins)

n_frames = 1 + (signals - frame_length) / frame_step
num_spectrogram_bins = fft_length//2+1

def stft(wav, win_length=640, win_step=640, n_fft=1024):'''stft 快速傅里叶变换Args:wav: *.wav的文件信息, float32, shape (16000,)win_length: 每一帧窗口的样本点数, int8win_step: 帧移的样本点数, int8n_fft: fft 系数, int8Returns:spectrograms: 快速傅里叶变换计算之后的语谱图shape: (n_frames, n_fft//2 + 1)n_frames = 1 + (signals - frame_length) / frame_stepnum_spectrogram_bins: spectrograms[-1], int8'''# if fft_length not given# fft_length = 2**N for integer N such that 2**N >= frame_length.# shape (25, 513)stfts = tf.signal.stft(wav, frame_length=win_length,frame_step=win_step, fft_length=n_fft)spectrograms = tf.abs(stfts)spectrograms = tf.square(spectrograms)# Warp the linear scale spectrograms into the mel-scale.num_spectrogram_bins = stfts.shape.as_list()[-1]  # 513return spectrograms, num_spectrogram_bins

tf.signal.stft(), 摘自tensorflow/python/ops/signal/spectral_ops.py

@tf_export('signal.stft')
def stft(signals, frame_length, frame_step, fft_length=None,window_fn=window_ops.hann_window,pad_end=False, name=None):# 各变量转成tensorwith ops.name_scope(name, 'stft', [signals, frame_length,frame_step]):signals = ops.convert_to_tensor(signals, name='signals')signals.shape.with_rank_at_least(1)frame_length = ops.convert_to_tensor(frame_length, name='frame_length')frame_length.shape.assert_has_rank(0)frame_step = ops.convert_to_tensor(frame_step, name='frame_step')frame_step.shape.assert_has_rank(0)if fft_length is None:# fft_length = 2**N for integer N such that 2**N >= frame_length.fft_length = _enclosing_power_of_two(frame_length)else:fft_length = ops.convert_to_tensor(fft_length, name='fft_length')# 分帧， shape=(1+(signals-frame_length)/frame_step, fft_length//2+1)framed_signals = shape_ops.frame(signals, frame_length, frame_step, pad_end=pad_end)# 加窗，默认是hanning窗if window_fn is not None:window = window_fn(frame_length, dtype=framed_signals.dtype)# 使用方式是矩阵相乘framed_signals *= window# fft_ops.rfft produces the (fft_length/2 + 1) unique components of the# FFT of the real windowed signals in framed_signals.return fft_ops.rfft(framed_signals, [fft_length])

2.1 分帧 & 填充

input : wav, shape = wav.shape

ouput : framed_signals, shape = (n_frames, frame_length)

代码：

framed_signals = shape_ops.frame(signals, frame_length, frame_step, pad_end=pad_end)

frame_length / frame_length的计算方法：
- 假设wav是16k的采样率，signals为采样的样本点数
$s i g n a l s = 16000 * 1000 / 1000 = 16000$
- window_size_ms为40ms，frame_length为一帧的样本点数
$frame\_length = 16000 * 40 / 1000 = 640$
- window_stride_ms为40ms，frame_step为帧移的样本点数
$frame\_step = 16000 * 40 / 1000$
此处无填充
- 假如pad_end为True，则最后一帧不足帧长的补上0
- 举个例子，signals=16000，frame_length=512，frame_step=180，
  
  pad_end=False时，n_frames为87，最后340个样本点不足一帧舍去；
  
  pad_end=True时，n_frames为89，最后340个样本点扩充为2帧，末尾补0

2.2 加窗

input : framed_signals, shape = (n_frames, frame_length)

output : framed_signals = (n_frames, frame_length)

代码：

# shape = (frame_length, )
window = window_fn(frame_length, dtype=framed_signals.dtype)# 使用方式是矩阵相乘
framed_signals *= window

为什么要加窗？

参考：语音信号的加窗处理

吉布斯效应：将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。这种现象称为吉布斯效应。

因为我们的帧在起始和结束肯定是会出现不连续情况的，那样这个信号在分帧之后，就会越来越背离原始信号，此时我们需要对信号进行加窗处理，目的很明显了，就是为了减少帧起始和结束的地方信号的不连续性问题。
- 使全局更加连续，避免出现吉布斯效应
- 加窗的目的是为了减少泄露，而非消除泄露
上面的说法太官方了，在知乎上看到一个更人性化的解释：怎样用通俗易懂的方式解释窗函数？
加窗的过程

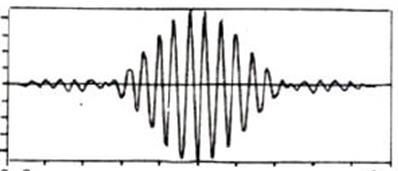
原始的时域信号和窗函数做乘积，输出的信号能够更好的满足傅里叶变换的周期性需求

* =
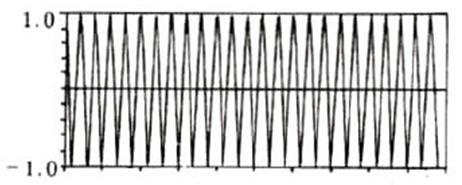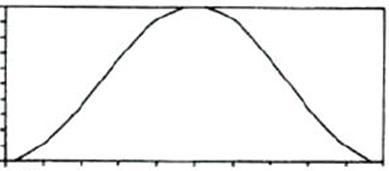窗函数使用的是汉宁窗，如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RvuYOO0b-1589366303382)(https://upload.wikimedia.org/wikipedia/commons/thumb/2/28/Window_function_%28hann%29.svg/220px-Window_function_%28hann%29.svg.png)]
$0.5\; \left(1 - \cos \left ( \frac{2 \pi t}{T} \right) \right)$
- tensorflow中实现的代码如下 tensorflow/python/ops/signal/window_ops.py：
```
# periodic 默认为1, a 默认为0.5， b 默认为0.5
even = 1 - math_ops.mod(window_length, 2)  # 1n = math_ops.cast(window_length + periodic * even - 1, dtype=dtype)  # 640
count = math_ops.cast(math_ops.range(window_length), dtype)
cos_arg = constant_op.constant(2 * np.pi, dtype=dtype) * count / nreturn math_ops.cast(a - b * math_ops.cos(cos_arg), dtype=dtype)
```

2.3 傅里叶变换

input : framed_signals, shape = (n_frames, frame_length)

output : spectrograms without padding, shape = (n_frames, num_spectrogram_bins)

由于信号在时域上的变换通常很难看出信号的特性，所以通常将它转换为频域上的能量分布来观察，不同的能量分布，就能代表不同语音的特性。对分帧加窗后的各帧信号进行做一个N点FFT来计算频谱，也称为短时傅立叶变换（STFT），其中N通常为256或512，NFFT＝512
$S_i(k)=\sum_{n=1}^{N}s_i(n)e^{-j2\pi kn/N} 1\le k \le K$

代码：numpy.fft.rfft(frames,NFFT)

fft_ops.rfft(framed_signals, [fft_length])

rfft 单独拎出来，来自github

# rfft
def rfft_wrapper(fft_fn, fft_rank, default_name):"""Wrapper around gen_spectral_ops.rfft* that infers fft_length argument."""def _rfft(input_tensor, fft_length=None, name=None):"""Wrapper around gen_spectral_ops.rfft* that infers fft_length argument."""with _ops.name_scope(name, default_name,[input_tensor, fft_length]) as name:input_tensor = _ops.convert_to_tensor(input_tensor,preferred_dtype=_dtypes.float32)fft_length = _ops.convert_to_tensor(fft_length)if input_tensor.dtype not in (_dtypes.float32, _dtypes.float64):raise ValueError("RFFT requires tf.float32 or tf.float64 inputs, got: %s" %input_tensor)real_dtype = input_tensor.dtypeif real_dtype == _dtypes.float32:complex_dtype = _dtypes.complex64else:assert real_dtype == _dtypes.float64complex_dtype = _dtypes.complex128input_tensor.shape.with_rank_at_least(fft_rank)
#       fft_length = Noneif fft_length is None:
#         fft_length = input_tensor.get_shape()[-1:]fft_shape = input_tensor.get_shape()[-fft_rank:]# If any dim is unknown, fall back to tensor-based math.if not fft_shape.is_fully_defined():fft_length = _array_ops.shape(input_tensor)[-fft_rank:]# Otherwise, return a constant.fft_length =  _ops.convert_to_tensor(fft_shape.as_list(), _dtypes.int32)else:fft_length = _ops.convert_to_tensor(fft_length, _dtypes.int32)# 此处对input_tensor做了一个填充, 末尾补零, 从frame_length 到 fft_lengthinput_tensor = _maybe_pad_for_rfft(input_tensor, fft_rank, fft_length)
#       print('\n')fft_length_static = _tensor_util.constant_value(fft_length)if fft_length_static is not None:fft_length = fft_length_staticreturn fft_fn(input_tensor, fft_length, Tcomplex=complex_dtype, name=name)_rfft.__doc__ = fft_fn.__doc__return _rfftrfft = rfft_wrapper(gen_spectral_ops.rfft, 1, 'rfft')
spec = rfft(framed_signals, [1024])
tf.abs(tmp)

在下找不到gen_spectral_ops.py这个文件啊

感兴趣的可以看一下numpy实现的傅里叶变换：numpy.fft.rfft(frames,NFFT)

小道消息，tensorflow2也是numpy实现，毕竟两者计算效果等同

2.4 对spectrum 取绝对值 & 平方

spectrograms = tf.abs(stfts)
spectrograms = tf.square(spectrograms)

0x03 梅尔滤波

input : spectrograms, shape=(n_frames, num_spectrogram_bins)

output : mel_spectrograms, shape=(n_frames, num_mel_bins)

Q：为什么要使用梅尔频谱？

A：频率的单位是赫兹（Hz），人耳能听到的频率范围是20-20000Hz，但人耳对Hz这种标度单位并不是线性感知关系。例如如果我们适应了1000Hz的音调，如果把音调频率提高到2000Hz，我们的耳朵只能觉察到频率提高了一点点，根本察觉不到频率提高了一倍。如果将普通的频率标度转化为梅尔频率标度，则人耳对频率的感知度就成了线性关系。也就是说，在梅尔标度下，如果两段语音的梅尔频率相差两倍，则人耳可以感知到的音调大概也相差两倍。

让我们观察一下从Hz到mel的映射图，由于它们是log的关系，当频率较小时，mel随Hz变化较快；当频率很大时，mel的上升很缓慢，曲线的斜率很小。这说明了人耳对低频音调的感知较灵敏，在高频时人耳是很迟钝的，梅尔标度滤波器组启发于此。

def build_mel(spectrograms, num_mel_bins, num_spectrogram_bins,sample_rate, lower_edge_hertz, upper_edge_hertz):'''构建梅尔滤波器Args:spectrograms: 语谱图 (1 + (wav-win_length)/win_step, n_fft//2 + 1)num_mel_bins: How many bands in the resulting mel spectrum.num_spectrogram_bins：An integer `Tensor`. How many bins there are in thesource spectrogram data, which is understood to be `fft_size // 2 + 1`,i.e. the spectrogram only contains the nonredundant FFT bins.sample_rate: An integer or float `Tensor`. Samples per second of the inputsignal used to create the spectrogram. Used to figure out the frequenciescorresponding to each spectrogram bin, which dictates how they are mappedinto the mel scale.sample_rate: 采样率lower_edge_hertz:Python float. Lower bound on the frequencies to beincluded in the mel spectrum. This corresponds to the lower edge of thelowest triangular band.upper_edge_hertz:Python float. The desired top edge of the highest frequency band.Returns:mel_spectrograms: 梅尔滤波器与语谱图做矩阵相乘之后的语谱图shape: (1 + (wav-win_length)/win_step, n_mels)'''linear_to_mel_weight_matrix = tf.signal.linear_to_mel_weight_matrix(num_mel_bins=num_mel_bins,num_spectrogram_bins=num_spectrogram_bins,sample_rate=sample_rate,lower_edge_hertz=lower_edge_hertz,upper_edge_hertz=upper_edge_hertz)################ 官网教程中, 少了sqrt #############spectrograms = tf.sqrt(spectrograms)mel_spectrograms = tf.tensordot(spectrograms,linear_to_mel_weight_matrix, 1)# 两条等价# mel_spectrograms = tf.matmul(spectrograms, linear_to_mel_weight_matrix)# shape (25, 40)mel_spectrograms.set_shape(spectrograms.shape[:-1].concatenate(linear_to_mel_weight_matrix.shape[-1:]))return mel_spectrograms

# 官方代码from __future__ import absolute_import
from __future__ import division
from __future__ import print_functionfrom tensorflow.python.framework import dtypes
from tensorflow.python.framework import ops
from tensorflow.python.framework import tensor_util
from tensorflow.python.ops import array_ops
from tensorflow.python.ops import math_ops
from tensorflow.python.ops.signal import shape_ops
from tensorflow.python.util.tf_export import tf_export_MEL_BREAK_FREQUENCY_HERTZ = 700
_MEL_HIGH_FREQUENCY_Q = 1127def _hertz_to_mel(frequencies_hertz, name=None):"""Converts frequencies in `frequencies_hertz` in Hertz to the mel scale.Args:frequencies_hertz: A `Tensor` of frequencies in Hertz.name: An optional name for the operation.Returns:A `Tensor` of the same shape and type of `frequencies_hertz` containingfrequencies in the mel scale."""with ops.name_scope(name, 'hertz_to_mel', [frequencies_hertz]):frequencies_hertz = ops.convert_to_tensor(frequencies_hertz)return _MEL_HIGH_FREQUENCY_Q * math_ops.log(1.0 + (frequencies_hertz / _MEL_BREAK_FREQUENCY_HERTZ))@tf_export('signal.linear_to_mel_weight_matrix')
def linear_to_mel_weight_matrix(num_mel_bins=20,num_spectrogram_bins=129,sample_rate=8000,lower_edge_hertz=125.0,upper_edge_hertz=3800.0,dtype=dtypes.float32,name=None):with ops.name_scope(name, 'linear_to_mel_weight_matrix') as name:# Convert Tensor `sample_rate` to float, if possible.if isinstance(sample_rate, ops.Tensor):maybe_const_val = tensor_util.constant_value(sample_rate)if maybe_const_val is not None:sample_rate = maybe_const_val# This function can be constant folded by graph optimization since there are# no Tensor inputs.sample_rate = math_ops.cast(sample_rate, dtype, name='sample_rate')lower_edge_hertz = ops.convert_to_tensor(lower_edge_hertz, dtype, name='lower_edge_hertz')upper_edge_hertz = ops.convert_to_tensor(upper_edge_hertz, dtype, name='upper_edge_hertz')zero = ops.convert_to_tensor(0.0, dtype)# HTK excludes the spectrogram DC bin.bands_to_zero = 1nyquist_hertz = sample_rate / 2.0# 间隔 (nyquist_hertz - zero) / (num_spectrogram_bins-1)# shape = (512, )linear_frequencies = math_ops.linspace(zero, nyquist_hertz, num_spectrogram_bins)[bands_to_zero:]# herz to mel# shape = [512, 1]spectrogram_bins_mel = array_ops.expand_dims(_hertz_to_mel(linear_frequencies), 1)# Compute num_mel_bins triples of (lower_edge, center, upper_edge). The# center of each band is the lower and upper edge of the adjacent bands.# Accordingly, we divide [lower_edge_hertz, upper_edge_hertz] into# num_mel_bins + 2 pieces.# shape = ((num_mel_bins + 2 - frame_length)/frame_step + 1, frame_length)band_edges_mel = shape_ops.frame(math_ops.linspace(_hertz_to_mel(lower_edge_hertz),_hertz_to_mel(upper_edge_hertz),num_mel_bins + 2), frame_length=3, frame_step=1)# Split the triples up and reshape them into [1, num_mel_bins] tensors.lower_edge_mel, center_mel, upper_edge_mel = tuple(array_ops.reshape(t, [1, num_mel_bins]) for t in array_ops.split(band_edges_mel, 3, axis=1))# Calculate lower and upper slopes for every spectrogram bin.# Line segments are linear in the mel domain, not Hertz.lower_slopes = (spectrogram_bins_mel - lower_edge_mel) / (center_mel - lower_edge_mel)print(lower_slopes)upper_slopes = (upper_edge_mel - spectrogram_bins_mel) / (upper_edge_mel - center_mel)# Intersect the line segments with each other and zero.mel_weights_matrix = math_ops.maximum(zero, math_ops.minimum(lower_slopes, upper_slopes))print(mel_weights_matrix)# Re-add the zeroed lower bins we sliced out above.# 补上bands_to_zero 行， 内容为0return array_ops.pad(mel_weights_matrix, [[bands_to_zero, 0], [0, 0]], name=name)melbank = linear_to_mel_weight_matrix(num_mel_bins=40,num_spectrogram_bins=513,sample_rate=16000,lower_edge_hertz=20.0,upper_edge_hertz=4000.0,dtype=dtypes.float32,name=None)

3.1 构造梅尔滤波器组（每一帧抽取40个特征）

output : linear_to_mel_weight_matrix, shape=(num_spectrogram_bins, num_mel_bins)

代码：

linear_to_mel_weight_matrix = tf.signal.linear_to_mel_weight_matrix(num_mel_bins=num_mel_bins,num_spectrogram_bins=num_spectrogram_bins,sample_rate=sample_rate,lower_edge_hertz=lower_edge_hertz,upper_edge_hertz=upper_edge_hertz)

3.2 计算梅尔滤波器的参数

3.2.1 转换

使用了Hidden Markov Model Toolkit (HTK)转换，
频率到梅尔频率的转换公式如下：
- 20 Hz —> 31.75 Mel
- 4000 Hz —> 2146.0756 Mel

$M (f) = 1127 l n (1 + f / 700)$

# tf2 实现代码
Mel = _MEL_HIGH_FREQUENCY_Q * math_ops.log(1.0 + (frequencies_hertz / _MEL_BREAK_FREQUENCY_HERTZ))

梅尔频率到频率的转换公式：

$M^{−1}(m)=700(e^{m/1127}−1)$

# tf2 实现代码
Herze = _MEL_BREAK_FREQUENCY_HERTZ * (math_ops.exp(mel_values / _MEL_HIGH_FREQUENCY_Q) - 1.0)

3.2.2 均等划分

一共有40个滤波器，num_mel_bins=40，需要42个点，包含最大和最小频率和中间等间距的点，在Mel空间上平均的分配：
$m (i) = 31.75, 83.32, 134.89, 186.46, 238.03, 289.59, 341.16, . . ., 2094.51, 2146.08$

# tf2 代码实现
math_ops.linspace(_hertz_to_mel(lower_edge_hertz),_hertz_to_mel(upper_edge_hertz),num_mel_bins + 2)# 自定义校验代码
mel = [np.round((31.75+i*(2146.0756 - 31.75)/41), 2) for i in range(42)]

3.2.3 分帧，分出前中后三个滤波器参数

shape = ((num_mel_bins + 2 - frame_length)/frame_step + 1, frame_length)

计算公式在上面有给出。输出40帧，每帧三个样本点。

band_edges_mel = shape_ops.frame(math_ops.linspace(_hertz_to_mel(lower_edge_hertz),_hertz_to_mel(upper_edge_hertz),num_mel_bins + 2), frame_length=3, frame_step=1)

分出三个边缘滤波器， shape = (1， (num_mel_bins + 2 - frame_length)/frame_step + 1)

# Split the triples up and reshape them into [1, num_mel_bins] tensors.
lower_edge_mel, center_mel, upper_edge_mel = tuple(array_ops.reshape(t, [1, num_mel_bins]) for t in array_ops.split(band_edges_mel, 3, axis=1))

3.2.4 建立滤波器

滤波器是三角滤波器，第一个滤波器从第一点开始，第二个时取得最大值，第三个点又归零。第二个滤波器从第二个点开始，第三点时达到最大值，第四点归零，依次类推。由下面的公式表达， $H_m(k)$ 表示其中一个滤波器：
$H_m(k)=\begin{cases} 0 &k \lt f(m-1) \\ \frac{k-f(m-1)}{f(m)-f(m-1)} & f(m-1) \le k \le f(m) \\ \frac{f(m+1)-k}{f(m+1)-f(m)} &f(m) \le k \le f(m+1) \\ 0 &k \gt f(m+1) \end{cases}$

m 表示滤波器的数量，$ f() $表示m+2梅尔间隔频率（Mel-spaced frequencies）列表。

代码中产生一个(512, 40) 的矩阵，每一列就是每一个滤波器，总共有40个滤波器

# Calculate lower and upper slopes for every spectrogram bin.
# Line segments are linear in the mel domain, not Hertz.
# 用到了广播， shape = ((512, 1) - (1, 40)) / ((1,40) - (1,40)) = (512, 40)
lower_slopes = (spectrogram_bins_mel - lower_edge_mel) / (center_mel - lower_edge_mel)
upper_slopes = (upper_edge_mel - spectrogram_bins_mel) / (upper_edge_mel - center_mel)# Intersect the line segments with each other and zero.
mel_weights_matrix = math_ops.maximum(zero, math_ops.minimum(lower_slopes, upper_slopes))# 填充bands_to_zero个维度
array_ops.pad(mel_weights_matrix, [[bands_to_zero, 0], [0, 0]], name=name)

# 画图代码
import matplotlib.pyplot as pltfreq = []  # 采样频率值
df = sample_rate / num_spectrogram_bins
for n in range(0, num_spectrogram_bins):freqs = int(n * df)freq.append(freqs)# x y 轴数据
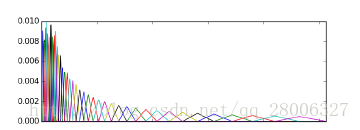
for i in range(1, num_mel_bins + 1):plt.plot(freq, melbank[:, i-1])plt.xlim((0, 8000))
plt.ylim((0, 1))plt.xlabel('frequency(Hz)', fontsize=13)
plt.ylabel('amplititude', fontsize=13)
plt.title("The 40-filter Mel Filterbank")
plt.show()

最终得到40个滤波器组，如下图所示：

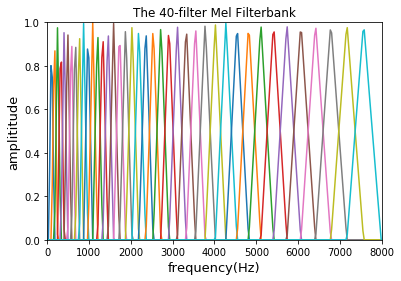
3.3 矩阵乘法

input: spectrograms, shape=(n_frames, num_spectrogram_bins)

output: mel_spectrograms, shape=(n_frames, num_mel_bins)

$n\_frames, n\_mels ，(n\_bins // 2 +1) ] * [ (n\_bins // 2 +1) ] = [ n\_frames, n\_mels]$

代码：

spectrograms = tf.sqrt(spectrograms)
mel_spectrograms = tf.matmul(spectrograms, linear_to_mel_weight_matrix)

官网给出的例子当中就是少了个sqrt()，导致计算结果出错，换句话说，前边不需要square()计算

0x04 进行log变换

Q: 为什么要进行log变换?

求对数后把小信号与大信号的差距变小了，原来两者相差10^{5倍，经过求对数后，两者相差100db，100和10}5相比，两者差距被缩小了，对数谱更接近于人耳实际听音时的感觉。

def log(mel_spectrograms):# Compute a stabilized log to get log-magnitude mel-scale spectrograms.# shape: (1 + (wav-win_length)/win_step, n_mels)# 学术界又叫做filter_bankslog_mel_spectrograms = tf.math.log(mel_spectrograms + 1e-12)return log_mel_spectrograms

0x05 采用DCT得到MFCC

DCT的作用，为了获得频谱的倒谱，倒谱的低频分量就是频谱的包络，倒谱的高频分量就是频谱的细节

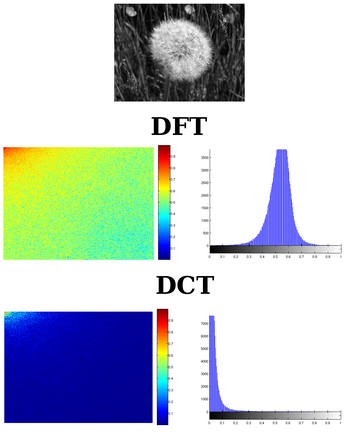
DCT 较之DFT的优势在于：

CT变换较DFT变换具有更好的频域能量聚集度（说人话就是能够把图像更重要的信息聚集在一块），那么对于那些不重要的频域区域和系数就能够直接裁剪掉

维基百科：

离散余弦变换（英语：discrete cosine transform, DCT）是与傅里叶变换相关的一种变换，类似于离散傅里叶变换，但是只使用实数。

2d DCT（type II）与离散傅里叶变换的比较：

将 $f_{0}$ 再乘以 ${\frac {1}{\sqrt {2}}}$ 。这将使得DCT-II成为正交矩阵.
$f_m = \sum_{k=0}^{n-1} x_k \cos \le[\frac{\pi}{n} m \le(k+\frac{1}{2}) ]$

def dct(log_mel_spectrograms, dct_counts):# shape (1 + (wav-win_length)/win_step, dct)mfccs = tf.signal.mfccs_from_log_mel_spectrograms(log_mel_spectrograms)# 取低频维度上的部分值输出，语音能量大多集中在低频域，数值一般取13。mfcc = mfccs[..., :dct_counts]return mfcc

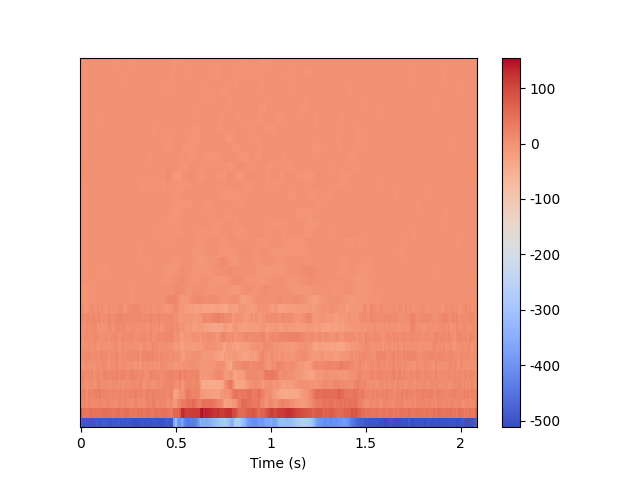
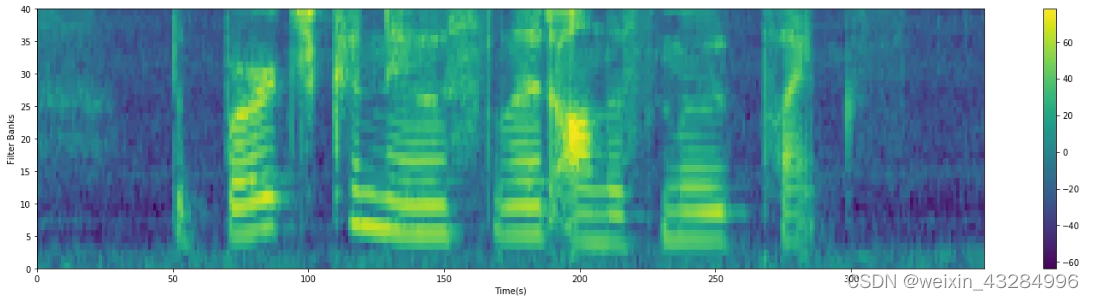
最终结果的mfcc 热力图

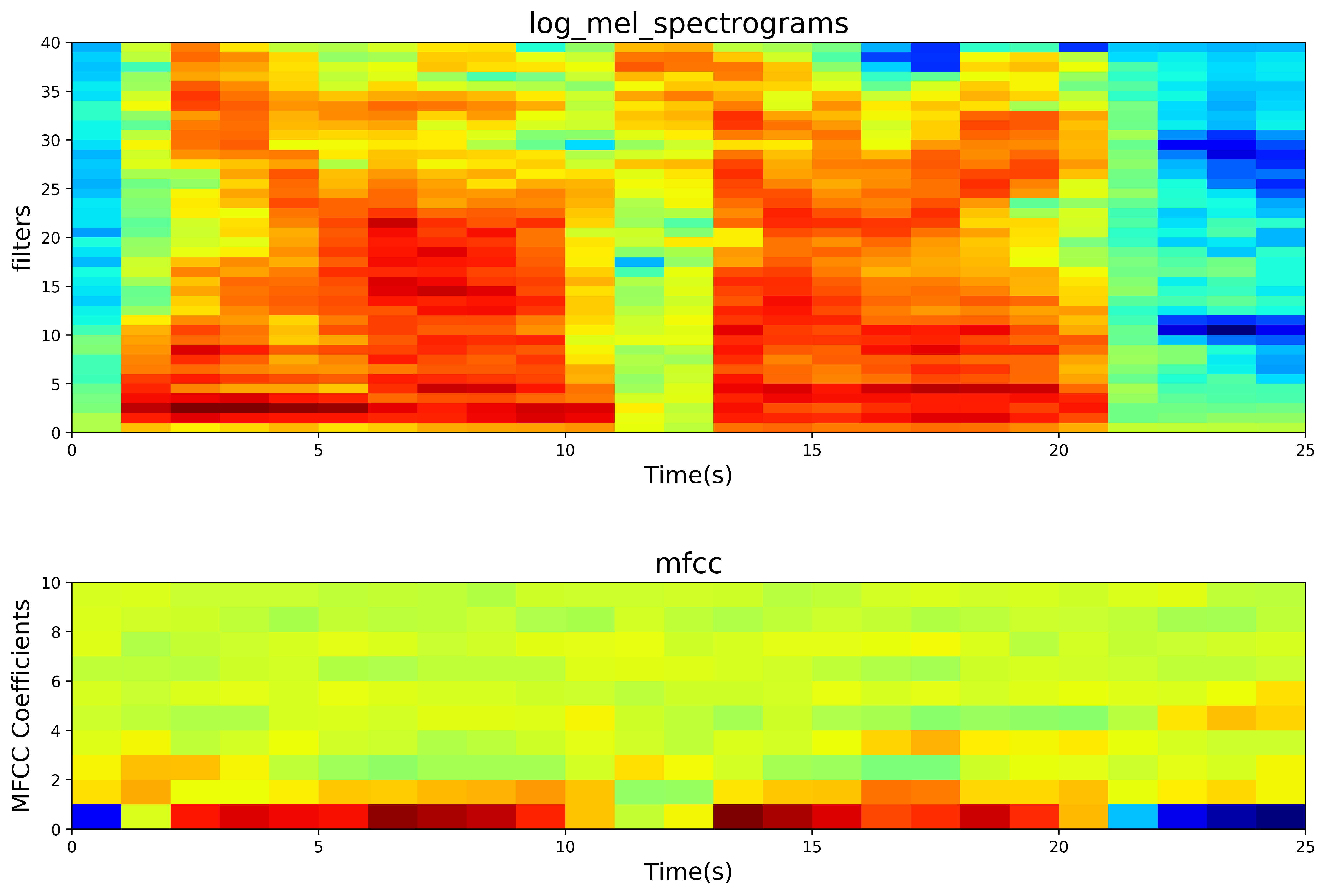
# 画图部分代码import matplotlib.pyplot as plt# %matplotlib inline
# %config InlineBackend.figure_format = 'png'# 保证时域是x轴
filter_bank = tf.transpose(log_mel_spectrograms)
# 保证时域是x轴，也是水平的
mfcc = tf.transpose(mfccs)plt.figure(figsize=(14,10), dpi=500)plt.subplot(211)
plt.imshow(np.flipud(filter_bank), cmap=plt.cm.jet, aspect='auto',extent=[0,filter_bank.shape[1],0,filter_bank.shape[0]])
plt.ylabel('filters', fontsize=15)
plt.xlabel('Time(s)', fontsize=15)
plt.title("log_mel_spectrograms", fontsize=18)plt.subplot(212)
plt.imshow(np.flipud(mfcc), cmap=plt.cm.jet,aspect=0.5, extent=[0,mfcc.shape[1],0,mfcc.shape[0]])
plt.ylabel('MFCC Coefficients', fontsize=15)
plt.xlabel('Time(s)', fontsize=15)
plt.title("mfcc", fontsize=18)# plt.savefig('mfcc_04.png')

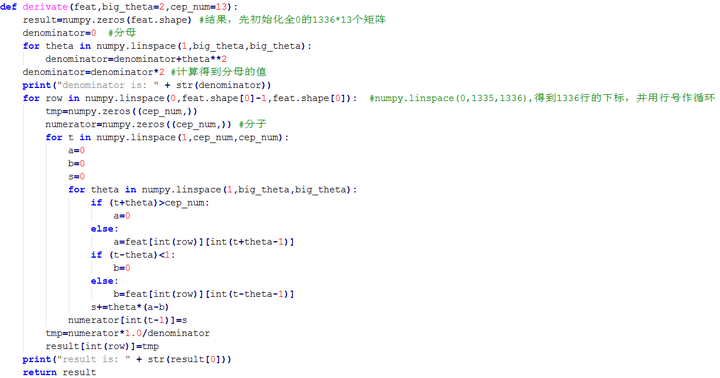
代码中的公式：
$\mathrm{Re}\Bigl\lbrace 2*e^{-j\pi \frac{k}{2N}} *FFT\lbrace y(n)\rbrace\Bigr\rbrace$

知乎，DFT到DCT，很详细，从DFT一步一步推导，最终的DCT公式如下：

推导证明DFT和DCT等价， $n = m^{'} - 1 / 2$

# tensorflow/python/ops/signal/mfcc_ops.py，
# mfccs_from_log_mel_spectrograms() 源码实现
dct2 = dct_ops.dct(log_mel_spectrograms, type=2)# 正交归一化
# DCT进行矩阵运算时，通常取sqrt(1/2N)
# rsqrt：取sqrt()的倒数； num_mel_bins = 40
return dct2 * math_ops.rsqrt(math_ops.cast(num_mel_bins, dct2.dtype) * 2.0)# tensorflow/python/ops/signal/dct_ops.py 
# dct_ops.dct 源码实现
scale = 2.0 * _math_ops.exp(_math_ops.complex(zero, -_math_ops.range(axis_dim_float) * _math.pi * 0.5 /axis_dim_float))# TODO(rjryan): Benchmark performance and memory usage of the various
# approaches to computing a DCT via the RFFT.
# 2 * axis_dim 将信号扩大为原来的两倍，目的是用实信号造一个实偶信号
# _math_ops.real() 返回复数的实数部分
dct2 = _math_ops.real(fft_ops.rfft(input, fft_length=[2 * axis_dim])[..., :axis_dim] * scale)return dct2