从倒谱图出发

• MFCC是Mel Frequency Cepstral Coefficient的简称，要理解MFCC特征，就需要先明白这里引入的一个新的概念——Cepstral，这个形容词的名词形式为Cepstrum，即倒谱图（频谱图Spectrum前四个字母倒着拼）
• 倒谱图是用来“提取”语音的音色（timbre）的，音色是区分说话人最有力的特征，尤其是在前深度学习时代。先直接给出求倒谱图的公式：
  $$C[x(n)]=F^{-1}[log(|F[x(n)]{|}^2)]$$
• 其中$x(n)$是离散化的原始信号，$F[\cdot ]$是离散傅里叶变换，$log(|\cdot {|}^2)$对离散傅里叶变换的结果，先取幅值，再取平方，最后取对数，$F^{-1}[\cdot ]$是离散傅里叶逆变换。
  下面是每一步的演示图：
  
  
  
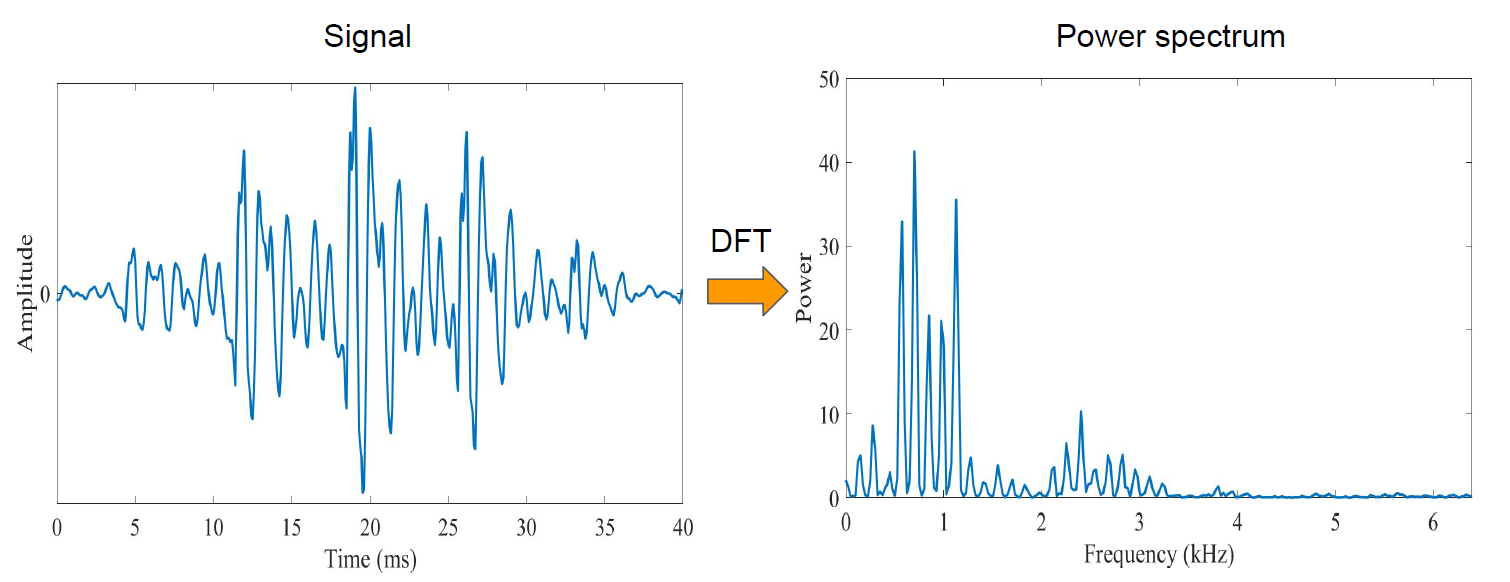
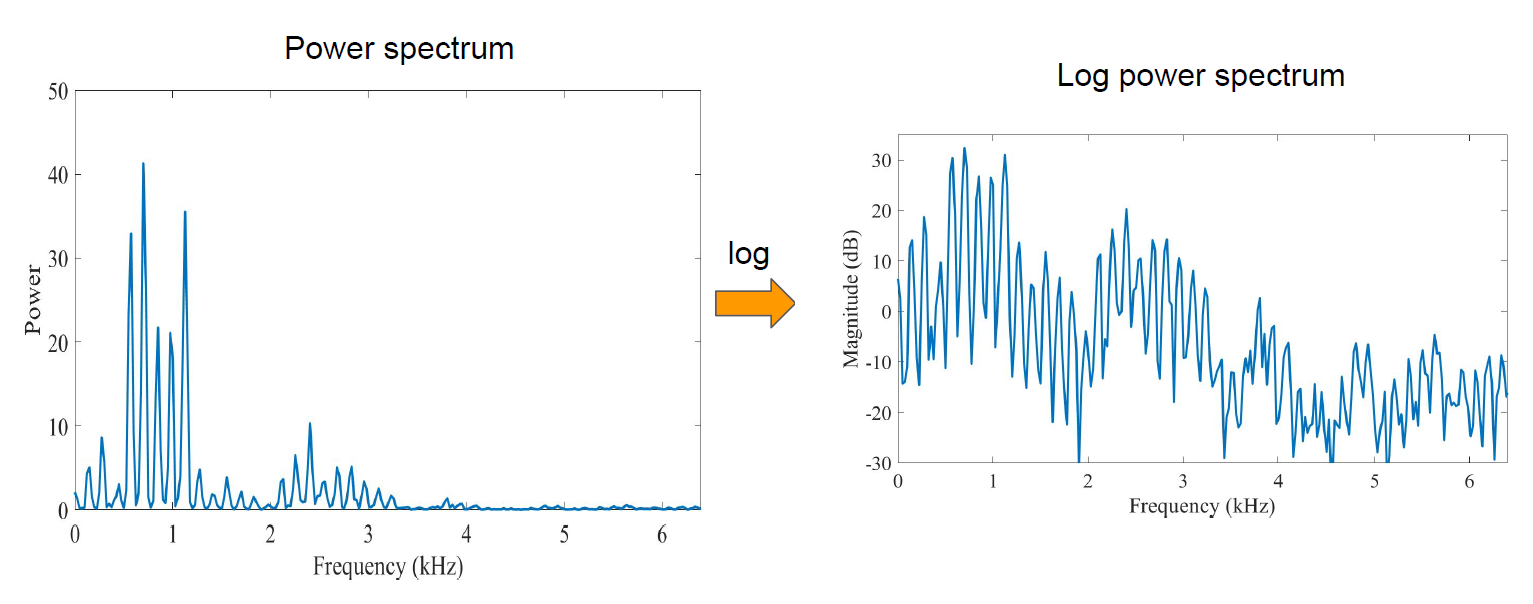
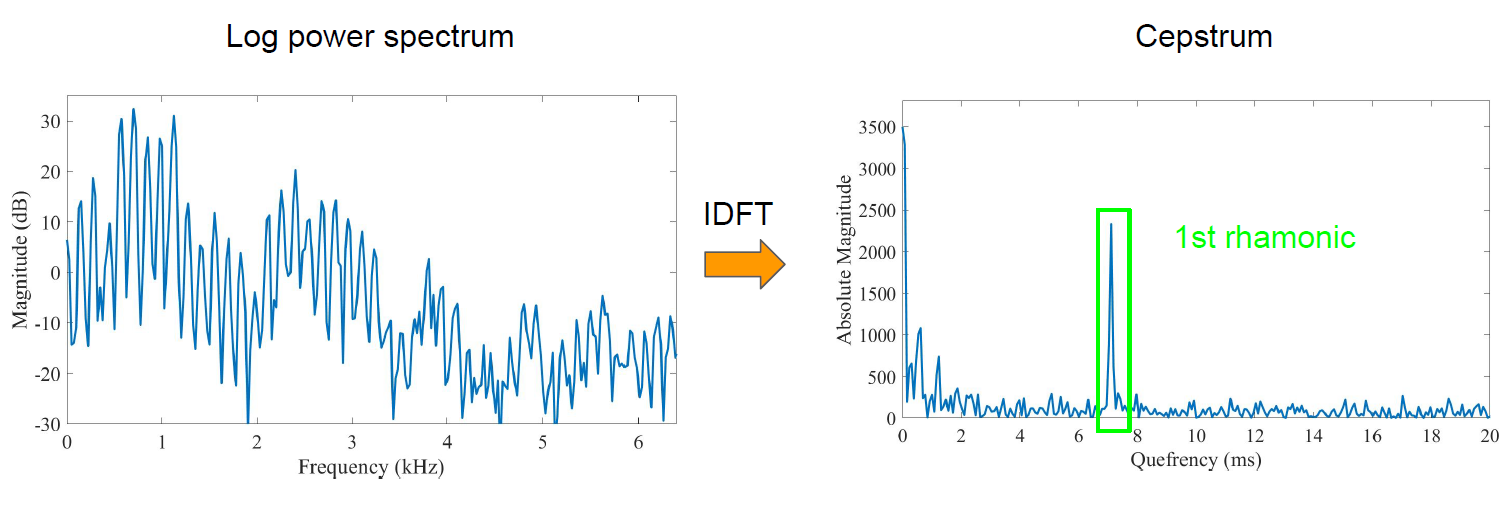
• 最后逆变换得到的倒谱图，横坐标为倒频率（Quefrency，频率的倒数，单位是秒），纵坐标是振幅。
• 最后一张图中的所谓1st rhamonic，是从倒谱图的右边往左看的第一个尖峰，实际上，这个1st rhamonic对应原始信号的基频。
• 要理解本节的内容，需要有离散傅里叶变换和梅尔时频谱图的知识，可以参考深入理解傅里叶变换（三）和深入理解梅尔刻度、梅尔滤波器组和梅尔时频谱图。

为什么倒谱图能提取音色

• 最初发出振动从而产生声音的物体，被称为声源，对于语音而言，声源就是人的声带。
• 人的肺部排出气体，这些气体通过声门（glottis），形成脉冲（glottis pulse），此时的脉冲频率决定了声音的音高，脉冲使声带振动，声带具有共振频率，会加强该脉冲。因为声源就是人的声带，所以声带的共振频率，称为此时这段语音的基频。
• 该脉冲还需要通过声道（vocal tract）才能从人的口中离开，成为能听到的语音。声道具有共振频率，随着声道的形状和大小变化，共振频率会发生变化，声道的共振频率的存在，使语音信号出现共振峰。
• 声门脉冲、基频和共振峰、声强，对应声音的三要素：音高、音色、响度。
  
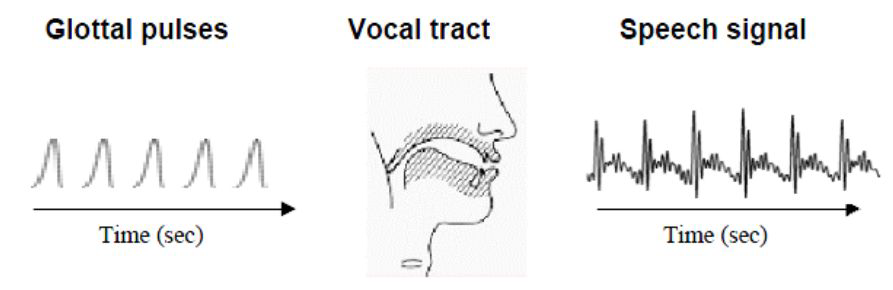
• 那么倒谱图为什么能提取音色呢？我们想象最开始通过声门的气体，是一种信号，称为Glottal pulses，记为$h(t)$，声带和声道的作用等效为一个复杂的滤波器，记为$e(t)$，输出的语音信号是Glottal pulses被声道滤波后的信号，记为$x(t)$，注意，此时都是连续信号，那么存在下列等式：
  $$x(t)=h(t)\ast e(t)$$
• 其中，$\ast$指卷积运算。离散化之后，再进行离散傅里叶变换，时域卷积等价于频域乘积：
  $$X(n)=H(n)\cdot E(n)$$
• 接下来，先取幅值，再取平方，最后取对数：
  $$log[|X(n){|}^2]=2log|H(n)|+2log|E(n)|$$
• 现在已经将语音信号，分解成两个信号的和了，如下图：
  
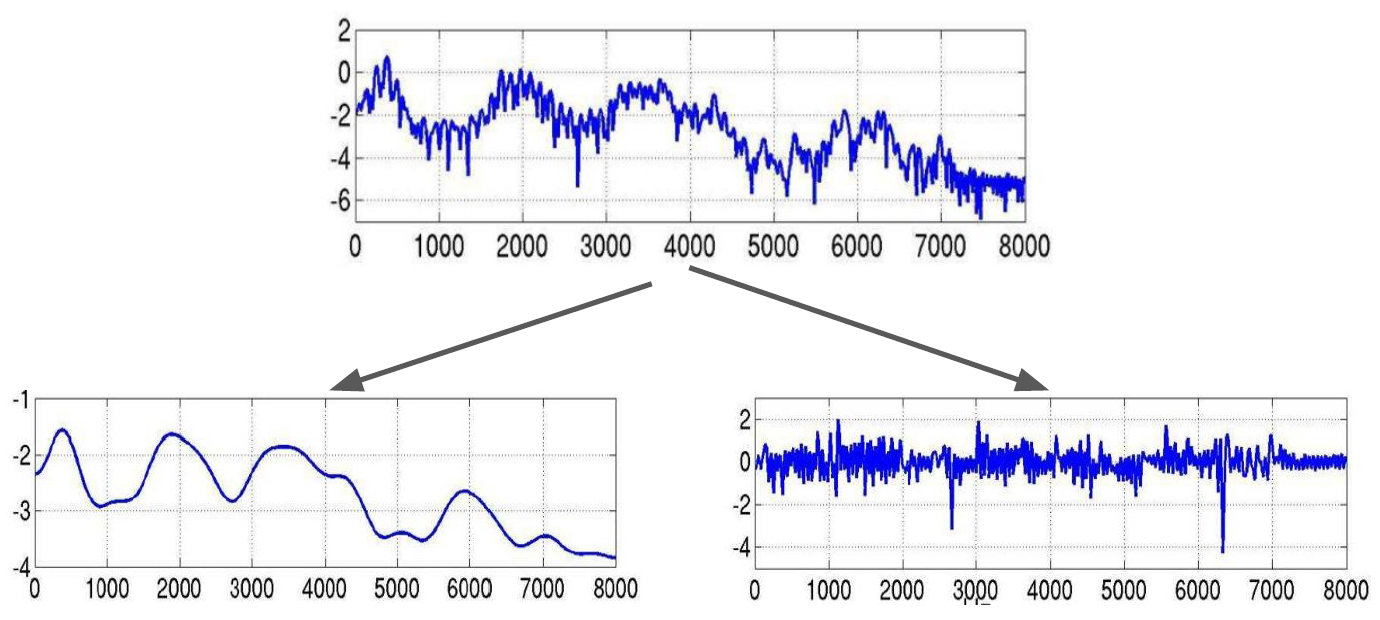
• 左下角是$2log|E(n)|$，右下角是$2log|H(n)|$，左下角实际上是语音信号的包络线，右下角是语音信号减去包络线之后的信号。其中，包络线有几个突起的峰（原本应该是尖峰，取对数之后平滑了），表征了基频和共振峰，是我们希望提取的信号。
• 最后一步是是用离散傅里叶逆变换，得到倒谱图。

MFCC

• 对于一段音频，MFCC的提取流程如下：
  1. 对音频信号进行预加重，从而降低部分高频能量。这一步可以简单采用下式处理：
     $$x[n]=x[n]-\alpha x[n-1],0.9\le \alpha \le 1.0$$
  2. 短时傅里叶变换
  3. 梅尔滤波器滤波，得到梅尔时频谱图
  4. 取对数，分离信号
  5. 离散余弦变换
  6. 选取倒谱系数
• MFCC的提取过程改良了最后一步，把离散傅里叶逆变换，改成了离散余弦变换。
• 因为log-power spectrum的信号，可以视为两个信号的叠加，而我们要提取的基频和共振峰，可以视为叠加后的信号的低频部分。
• 所以MFCC将log-power spectrum视为一种时域信号，对其进行傅里叶分析，然后取前 $n_{mfcc}$ 个频率所对应的运算值，作为最后的MFCC特征。
• 此外，使用离散余弦变换有如下的好处：
  • 是简化版的离散傅里叶变换
  • 运算结果是实数，正是MFCC所需要的
  • 解耦了不同梅尔滤波器组之间的重合权重，使提取出的特征更加相互独立，适用于机器学习
  • 输入log-power spectrum，输出MFCC特征，起到了降维作用

MFCC的输出

• 通常选取前12个系数，再拼接一个当前frame的能量，共13个。

• 越靠前的系数，包含越多的基频和共振峰的信息。

• 取得13个系数后，还会在时序上，对13个系数求一阶差分和二阶差分，二阶差分等价于对一阶差分求一阶差分。一阶差分有后向差分、前向差分的区别，也可以对后向差分和前向差分求均值得到中心差分，中心差分误差最小：

  • 前向差分
    $$\Delta x[n]=x[n+1]-x[n]$$
  • 后向差分
    $$\Delta x[n]=x[n]-x[n-1]$$
  • 中心差分
    $$\Delta x[n]=\frac{x[n+1]-x[n-1]}{2}$$

  其中，$x[n]$表示第n帧的13个系数，将一阶差分和二阶差分与原函数值拼接起来，得到39个系数。

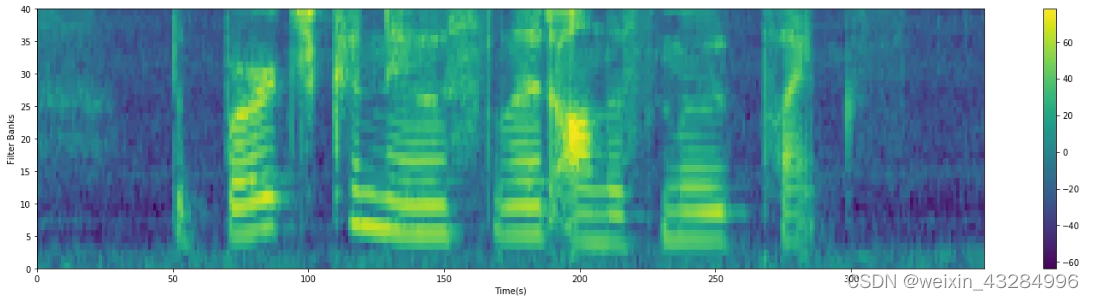
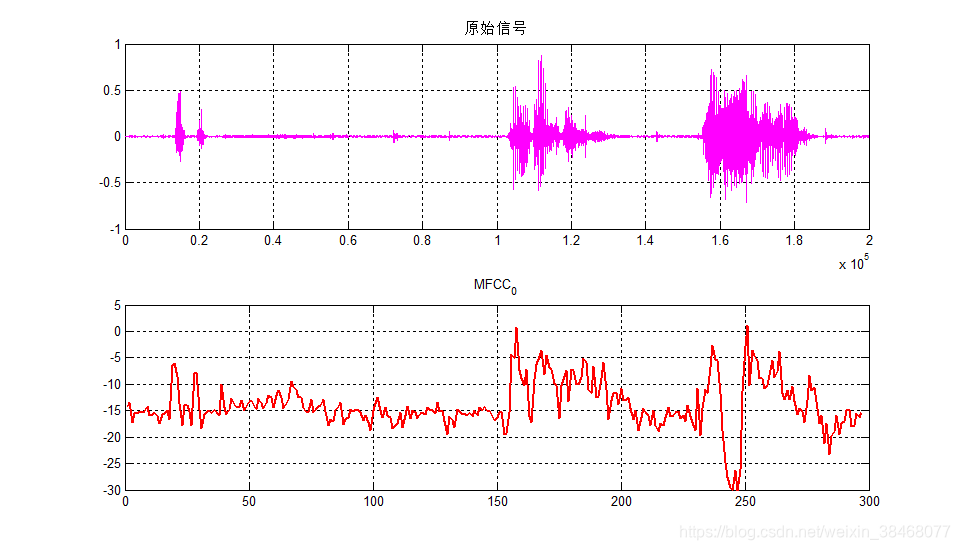
• MFCC的输出可以表示为一个二维数组，shape为$[n_{mfcc},frames]$，由于是二维数组，所以可以用热力图可视化。

MFCC的优缺点

• 优点
  • 相比较梅尔时频谱图，以更少的数据量描述了时频谱图的信息，前者滤波器个数通常为80，MFCC特征个数通常为39
  • 相比较梅尔时频谱图，特征之间的相关性更低，具有更好的区分性
  • 能提取出表征基频和共振峰的信息，滤去其他无关信息
  • 在基于GMM的声学模型中效果较好
• 缺点
  • 相比较梅尔时频谱图，计算量更大，因为MFCC是在梅尔时频谱图的基础上得到的
  • 对噪声，尤其是加性噪声，不够鲁棒
  • 人工设计的痕迹太重，导致更大的经验风险
  • 对语音合成无效，因为不存在从MFCC特征到音频信号的逆变换

演示

• 注意：librosa的MFCC提取算法，
  • 默认没有将当前frame的能量作为第13个系数，可以自行求，然后拼接
  • 此外，默认没有一阶差分和二阶差分，也可以自行求，然后拼接
• 下列代码就计算了一阶差分和二阶差分，然后拼接并可视化。

import librosa
import librosa.display
import matplotlib.pyplot as plt
import numpy as npif "__main__" == __name__:filepath = r"20- Extracting MFCCs with Python\female_audio.wav"signal, sr = librosa.load(path=filepath, sr=16000)N_FFT = 512N_MELS = 80N_MFCC = 13mel_spec = librosa.feature.melspectrogram(y=signal,sr=sr,n_fft=N_FFT,hop_length=sr // 100,win_length=sr // 40,n_mels=N_MELS)mfcc = librosa.feature.mfcc(S=librosa.power_to_db(mel_spec), n_mfcc=N_MFCC)delta_mfcc = librosa.feature.delta(data=mfcc)delta2_mfcc = librosa.feature.delta(data=mfcc, order=2)mfcc = np.concatenate([mfcc, delta_mfcc, delta2_mfcc], axis=0)librosa.display.specshow(data=mfcc,sr=sr,n_fft=N_FFT,hop_length=sr // 100,win_length=sr // 40,x_axis="s")plt.colorbar(format="%d")plt.show()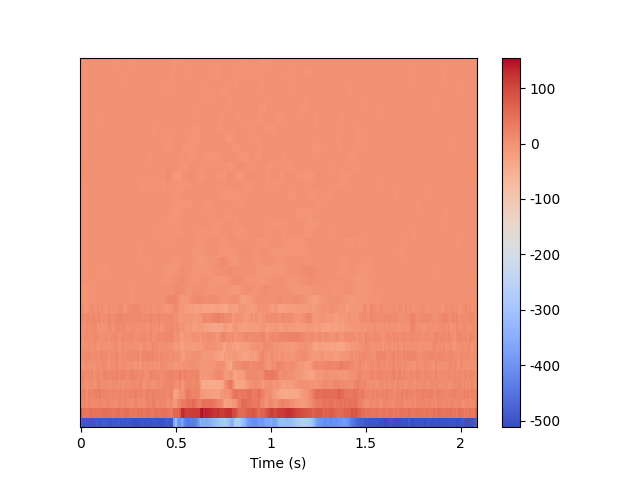

• 音频信号处理的知识非常广袤，本系列只讲解了用于机器学习的音频信号处理知识。