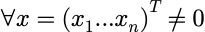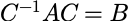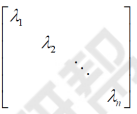线性代数基础知识点回顾与总结（一）：行列式与矩阵
介绍

• 骨骼图
  

1.行列式

排列： 1，2,···，n组成的有序数组称为n阶排列。

逆序：大数排在小数前。自然排列为偶排列。

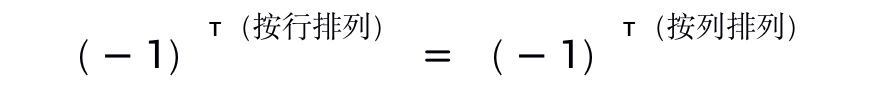
n阶行列式的值等于不同行的n个元素的乘积的代数和：

注 ：主对角元素减副对角元素的求法只适用于2或3阶行列式的计算中。

三角行列的值：

注：副主对角时要考虑正负号：

方阵行列式（n*n）:
$$|AB|=|A|\cdot |B|;|A^2|=|A{|}^2.$$

行列式：

1.交换两行位置正负号改变。

推论：

• 两行相同或成比例，行列式为0

2.某行k倍加到另一行，值不变。
3.

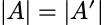
4.

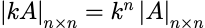
5. n阶行列式都可以写成两数之和，可以拆分成2^n个行列式之和。

例如2阶的：


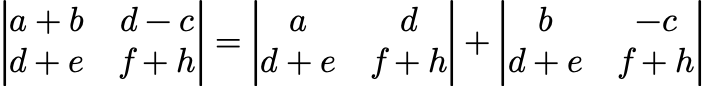
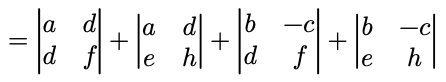
代数余子式（cofactor）

a(I,j)的代数余子式为）：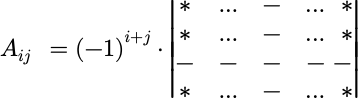
行列中_的意思是去掉第i行第j列，剩下的称为第（i,j）个元素的余子式。

行列式=某列（行）的每一个元素*它的代数余子式之和。
某行（列）元素与另一行（列）元素的代数余子式的乘积为0。

范德蒙行列（Vandermonde）

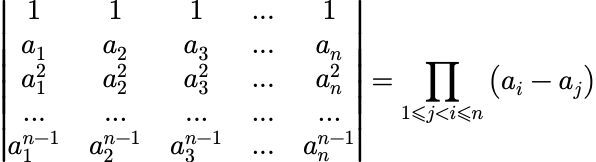
例子：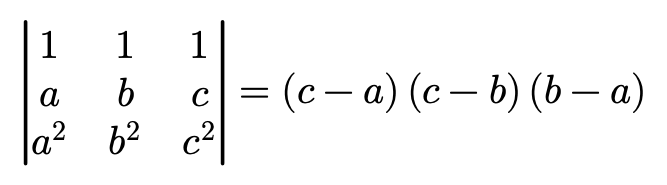
拉普拉斯定理（Laplace）

A、B、C都是行列。

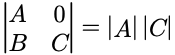
推广：

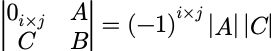
2.矩阵

矩阵：m*n个数排列成m行n列的表格。若m=n，则称为n阶矩阵。

克莱姆法则（Cramer’s Rule）：AX=b,若｜A｜≠0，则存在唯一的解，其解为：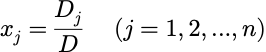
其中，D为系数矩阵的值。

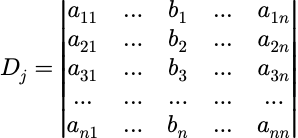
b在第j列。

对比齐次方程组AX=0，若｜A｜≠0，则只有0解。
若齐次方程组有非零解，则要求系数行列式|A|=0。

运算法则：

• A(BC)=A(BC)
• A(B+C)=AB+AC;
• (A+B)C=AC+BC;
• A(B+C)D=ABD+ACD

注：AB≠BA；AB=0(不能推出) A=0或B=0；AB=AC(不能推出)B=C

转置：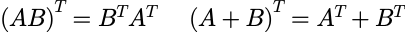
方阵

• 仅有方阵才有行列式
• 方阵A=0与|A|=0不要搞混

对称矩阵（symmetric matrix）：

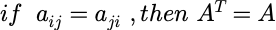
反矩阵（shew-symmetric matrix）：

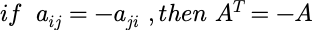
伴随矩阵（adjugate matrix）：

这里由于翻译、符号等问题，很多小朋友搞不清楚伴随矩阵、伴随变换。

伴随矩阵(adjugate) 指的是由矩阵的代数余子式构成的矩阵的转置，用A表示，严谨点可以用adj(A)表示，这样不会发生歧义。
伴随变换（adjoint）也称共轭变换，指的是共轭转置矩阵，也叫**埃尔米特矩阵（Hermitian Matri）**用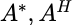
表示，国内用A表示伴随矩阵，因此用后者不会产生歧义。

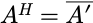
埃尔米特矩阵（Hermitian Matri）：

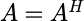
例如：

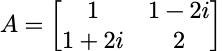
如果A，B都是埃尔米特矩阵，则A+B也是埃尔米特矩阵；如果满足交换律AB=BA，则AB也是埃尔米特矩阵。

共轭矩阵(conjugate) 指矩阵的所有元素取共轭，用conj(A)表示，或

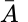
对于伴随矩阵：


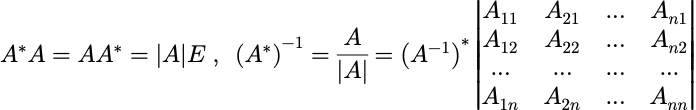
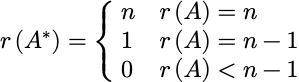
可逆矩阵（Invertible matrix）：

A·B=E (B为A的逆矩阵)（前提：A与B同阶）

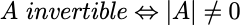
如果A,B可逆，则：

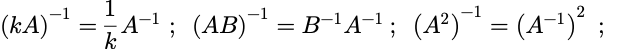
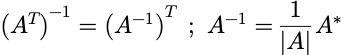
对角矩阵：

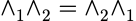
分块矩阵（partitioned matrix）
运算：


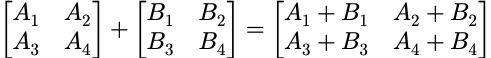
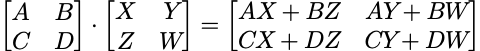
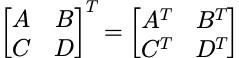
初等矩阵
单位矩阵经过一次初等变换得到的矩阵。
初等变换 ：

1. 倍乘
2. 倍加
3. 行互换

等价矩阵
A经过有限次初等变换得到B。A等价于B记为：

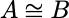
性质：

反身性，对称性，传递性：

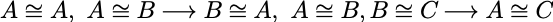
例：

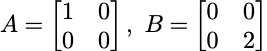
A，B等价：

行阶梯矩阵（Row-Echelon Form）:

1. 0行在最底部
2. 非0主元下面全为0

例：

行最简矩阵（Row-simplest form）:

非0主元都为1且上下全为0。
例：（主元下画了横线）

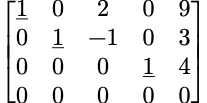
正交矩阵（Orthogonal matrix）

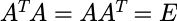
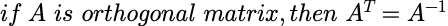
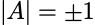
若矩阵A、B为正交矩阵，则AB也为正交矩阵。

任何对称矩阵、正交矩阵都可以被对角化。

这句话我们可以这样理解，正交矩阵可以看作三维空间中被随意摆放的立方体，而对角化就是将齐摆正。直观上讲就是，任何一个歪着的立方体，都可以被摆正。（当然在这里，我们不讨论虚数的情况。）

相似矩阵（Similarity matrix）

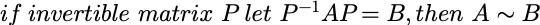
相似矩阵可以理解为同一个线性变换在不同基上的矩阵。

性质： 反身性，对称性，传递性

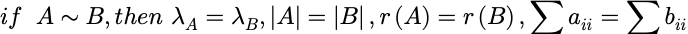
（如果从 相似矩阵是同一个线性变换在不同基上的矩阵 这个角度理解的换，上面结论将变得理所当然。）

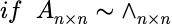
• A有n个线性无关的特征向量
• 若有k重特征值，则该特征值必有k个线性无关的特征向量。

实对称矩阵：

矩阵元素全为实数，且

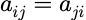
其特征值全为实数，不同特征值对应的特征向量必正交。

总存在正交矩阵Q，使得：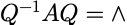
A与对角矩阵相似。A的特征值与对角矩阵主对角元素相同。