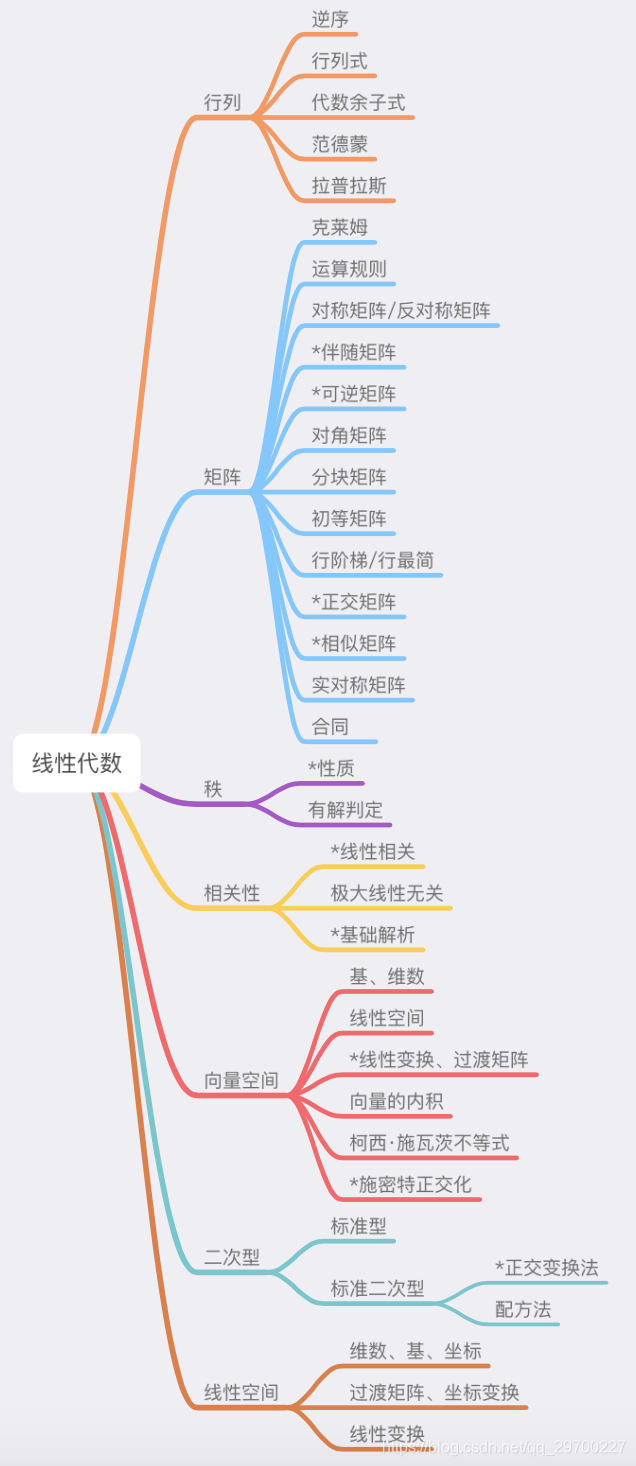
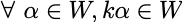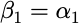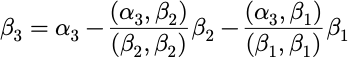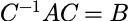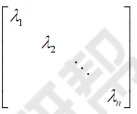基础线性代数知识点总结与回顾（三）：向量空间和二次型

骨骼图：

向量空间

对加法、数乘封闭。
W——n维向量的非空集合，且满足：

• 
• 

则：W为n维向量空间的子空间。

如果向量空间V中的向量(a1,a2,a3…am)满足：

• a1,a2,a3…am线性无关
• V中任意(贝塔)均可由a1,a2,a3…am线性表出。即：
  
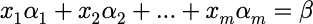
  则称a1,a2,a3…am是向量空间V的基，m是向量空间的维数，称V是m维向量空间。称x1,x2,…,xm是向量（贝塔）在基（a1,a2,a3…am）下的坐标。

过渡矩阵：

基（a1,a2,a3）——>基（b1,b2,b3）:
[b1,b2,b3]=[a1,a2,a3]*C，C称为过渡矩阵。

向量的内积：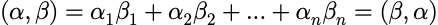



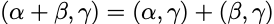
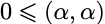
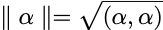
单位化：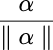
柯西-施瓦茨不等式：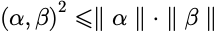
等号当且仅当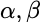线性相关时成立。
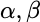正交，
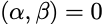
定理： 若n维向量a1,a2,…,an是一组两两正交的非零向量，则a1,a2,…,an线性无关。

施密特（Schmidt）正交化：
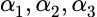线性无关：

• 
• 
• 

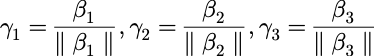
特征值(eignvalue)、特征向量(eignvector)：

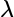为特征值，为特征向量。



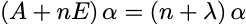
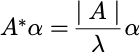
若A可逆：

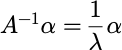
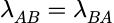但是AB与BA的特征向量不同。

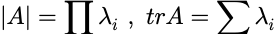
不同特征值对应的特征向量线性无关。
A可逆，A的n个特征值全不为0。

二次型

二次型及其矩阵表示：


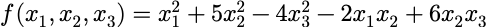
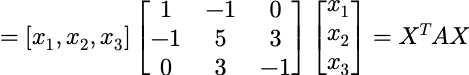
二次型的秩： r(f)=r(A)

合同： 如果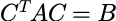，其中C可逆，称矩阵A、B合同，记：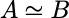
合同性质： 反身性，对称性，可传递性。

标准型：

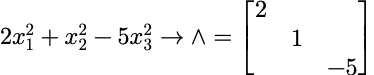
任何一个二次型都能通过坐标变换化成标准型。

• 配方法
• 正交变换（**重要）
  A实对称，存在正交矩阵Q，使得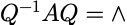
  这里Q可以看作特征向量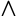，可以看作特征值组成的对角矩阵。
  为了更直观，上面式子可以进行变形：
  
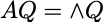
  这样就一目了然了。

定理： 任意一个二次型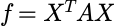，其中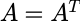
，总存在正交变换x=py,(p为A的特征向量，是正交矩阵)，使得二次型化为标准型：

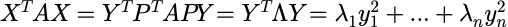
其中，是A的n个特征根。

规范性：
首先它必须是标准型，其次它只能由1，-1，0组成。
例如：

任意一个n元二次型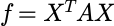都存在坐标变换X=CZ，使f化为规范型。

正惯性指数p，负惯性指数q（针对标准型）

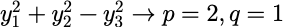
惯定性定理： 对一个二次型，经过坐标变换化为标准型，其正惯性指数p，负惯性指数q是唯一确定的。
实对称矩阵A和B合同（等价于）

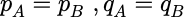
正定二次型： 设二次型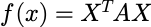
，如果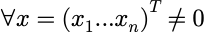
恒有f(x)>0，则称f为正定二次型，二次型矩阵A称为正定矩阵。（f(x)>=0：半正定）
是否与E合同是正定的必要条件。