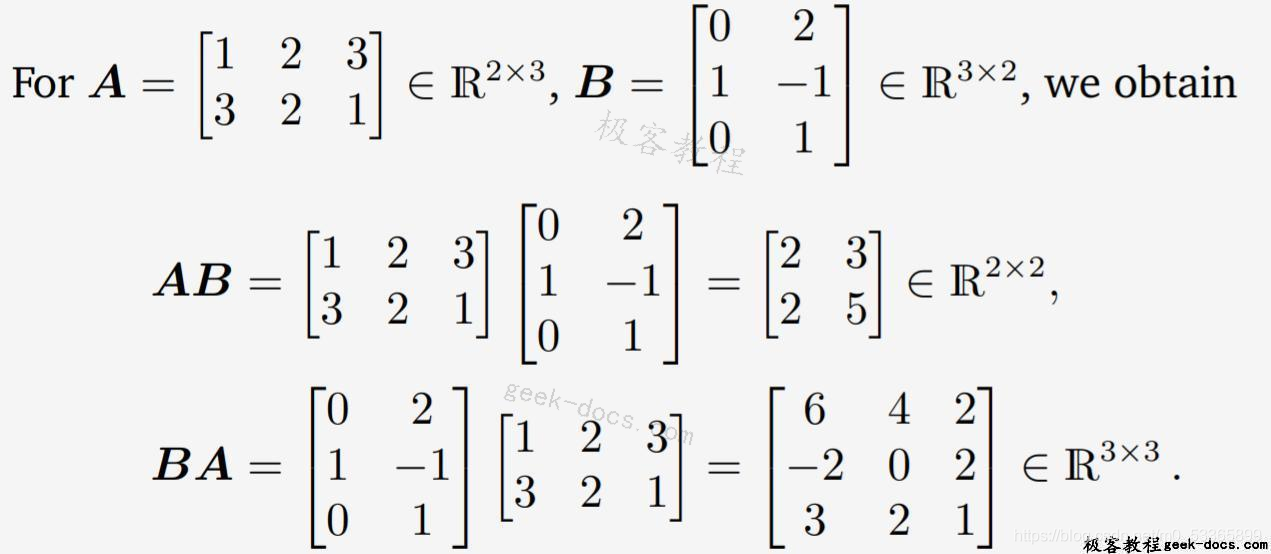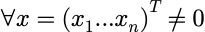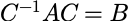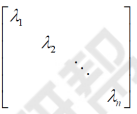（一），矩阵的基本概念

1，矩阵的定义

定义1，将m×n个数aij（矩阵的元素）(i=1,2,3…,m;j=1,2,…,n)排成m行n列的矩形数阵(为了表达这一整体，将其括以圆括号)
例:

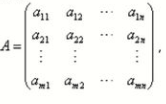
称为一个m行n列矩阵，或者称为m×n矩阵在不发生混淆的情况下，也简称为矩阵，通常用大写的黑体字母A,B,C…或（aij）,(bij),(cij)…表示矩阵

注意 1， 当矩阵的元素都为实数时矩阵为实矩阵
注意 2， 当矩阵的元素都为复数时矩阵为复矩阵
注意 3， 当矩阵的元素都为0时矩阵为零矩阵简记为0
​注意 4， 将1行n列的矩阵称为行矩阵或行向量
例:

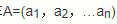
注意 5， 将1列n行的矩阵称为列矩阵或列向量
例:

注意 6， 将a11,a22,…,ann所在的对角线称为矩阵A的主对角线，而另外一条对角线称为A的副对角线

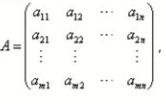
由于找不到n×n形式的图片所以假设上图中(m=n)

补充:通常用黑体希腊字母α，β表示列矩阵（向量），而用
αᵀ，βᵀ，…表示行矩阵（向量）。

注意7， 主对角线以下都为0的n阶方阵称为n阶上三角矩阵

例:

注意 8， 主对角线以上都为0的n阶方阵称为n阶下三角矩阵

注意 9， 将除了主对角线以外元素全为0的n阶方阵称为n阶对角矩阵
例:

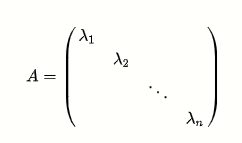
当对角矩阵的对角线上的元素都相等，则称这个矩阵为n阶标量矩阵当对角线上的元素都等于1，则称这个矩阵为n阶单位矩阵，简记为En也可简记为E

（二），矩阵的运算

1，矩阵的加减法

具体如下

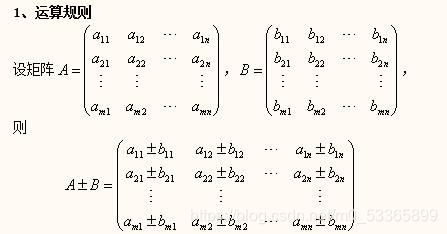
(1),结合律:(A+B)+C=A+(B+C).
(2),交换律:A+B=B+A.
(3),A+0=0+A=A

2，数与矩阵的乘法

例如:数k与矩阵A的乘积，简记为kA或Ak
(就是将矩阵中每一个元素都乘以一个系数k)

3，矩阵的乘法

例如:矩阵A与矩阵B相乘就是用矩阵B的列乘矩阵A的行。
反之:矩阵B与矩阵A相乘就是用矩阵A的列乘矩阵B的行
注意:不是任意两个矩阵都能够相乘，只有当第一个矩阵的列数等于第二个矩阵的行数时两个矩阵才能相乘，且当两个矩阵能够相乘时，得到的乘积矩阵的行数等于第一个矩阵的行数，列数等于第二个矩阵的列数

注意: 矩阵的乘法不一定满足交换律，也就是说AB不一定等于
BA
注意: 两个不为零的矩阵相乘可以是零矩阵，也就是说AB=0不一定等于A=0或B=0
注意: 消失律在矩阵乘法中不成立，也就是说AB=AC不一定能推出B=C.

矩阵乘法满足如下的规律：
（1）乘法结合律：（AB）C=A（BC）
（2）乘法与加法分配律：A（B+C）=AB+BC
（3）k（AB）=（kA）B= A（kB）(k为一个常数)

定理: 任意一个矩阵乘以单位矩阵都等于其本身
AEn=A,EmA=A
A0n=0,0mA=0
定理: 任意一个矩阵乘以零矩阵都为零矩阵

单位矩阵如下图

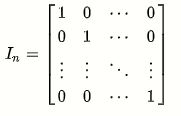
重点:仿造数的方幂，也可以定义矩阵的方幂
A^0(A的零次方)=E
A^1=A(A的一次方)
A^r+1=A*Ar
A^rAs =A^r+s(A的r次方乘A的s次方等于A的r+s次方)
（A^r）s=A^rs

************同时，矩阵乘法还可用于线性方程组中
将（x1,x2,x3…xn）被乘数作为一个被乘矩阵
而方程组系数可以作为一个矩阵去乘上述矩阵
线性方程组的答案也可作为一个矩阵等于以上两个矩阵相乘

4，矩阵的转置

1,（Aᵀ）ᵀ=A
2,（A+B）ᵀ=Aᵀ+Bᵀ
3,（kA）ᵀ=kAᵀ(k是一个常数)
4，(AB)ᵀ=BᵀAᵀ

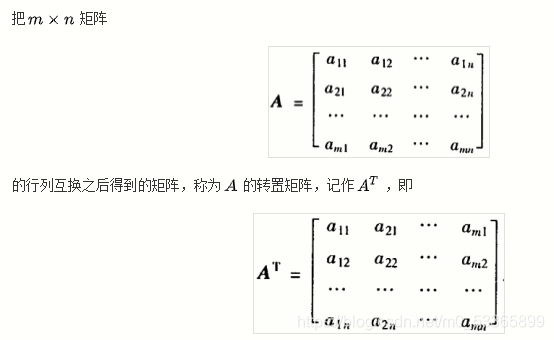
注意: 当矩阵为方阵时（这是前提）
Aᵀ=A,则称A为对称矩阵
Aᵀ=-A,则称A为反对称矩阵

5，方阵的行列式

运算规律如下:

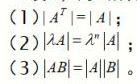
6，伴随矩阵

此定理可通过异乘变零定理推出
注：异乘变零定理是某行元素与另一个行的代数余子式相乘之和等于0。

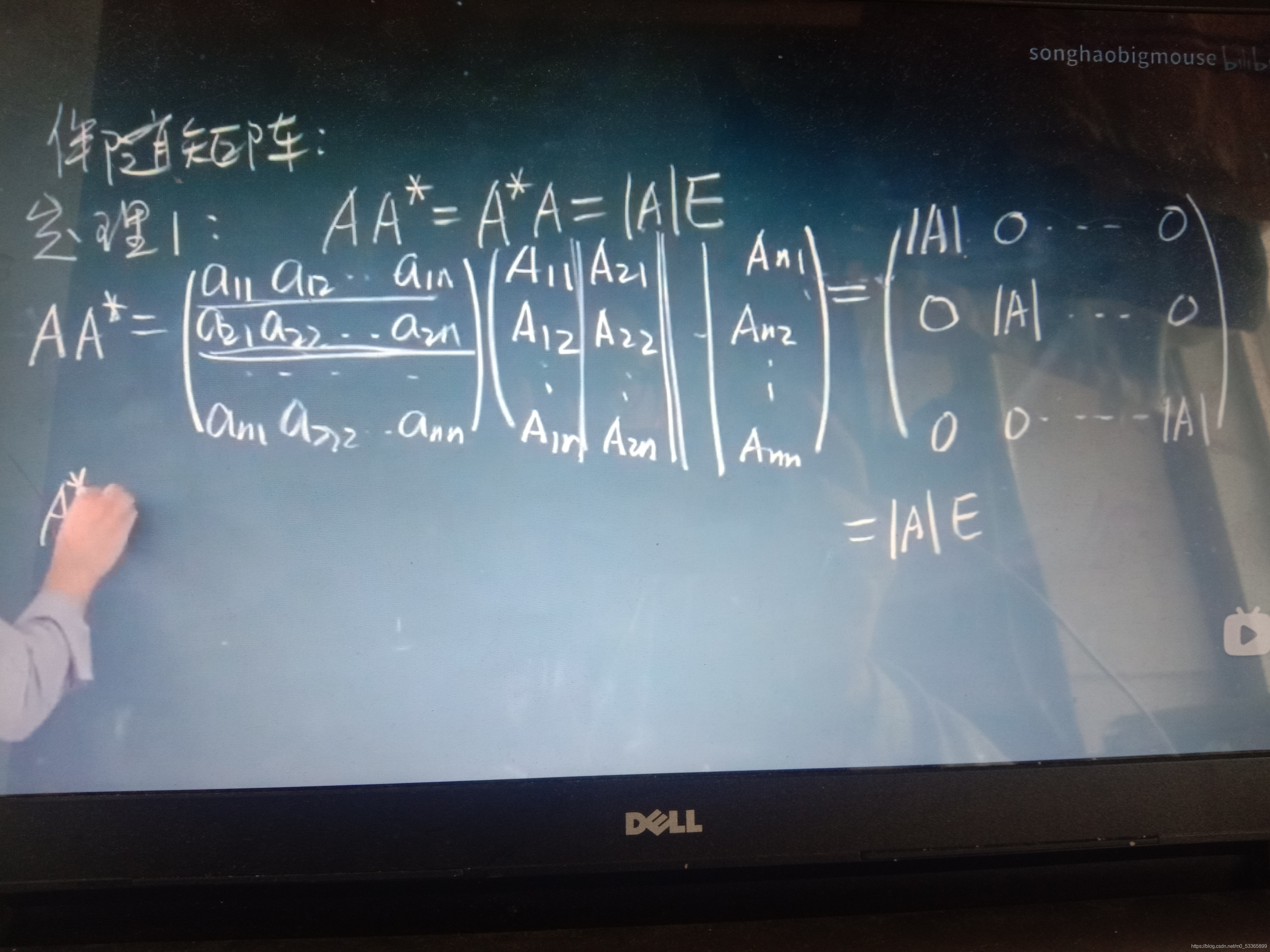
运算变形

（三），可逆矩阵的逆矩阵

1,可逆矩阵及其逆矩阵的定义

定义1，对于n阶方阵A，如果存在一个n阶方阵B,使得
AB=BA=E
定义2，假设矩阵B和C均为A的逆矩阵，则
AB=BA=E,AC=CA=E
B=BE=B(AC)=(BA)C=EC=C
总结：所以A的逆矩阵是唯一的

2，逆矩阵的判别

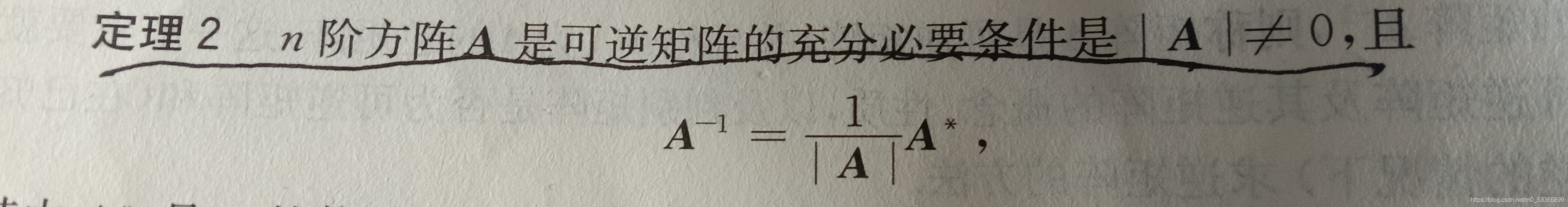
必要性–>设A是逆矩阵，于是存在一个n阶方阵B,使得AB=AB=E，对AB=E两边分别取行列式，得
|A||B|=|AB|=|E|=1
因此**|A|不等于0
然后通过之前伴随矩阵**的知识去变形即可图中的公式

充分性–>

补充：当|A|不等于0，则称A是非退化矩阵或非奇异矩阵；否则，即|A|=0时，则称A时退化矩阵或奇异矩阵

总结: n阶方阵A，如果A的行列式|A|是可逆矩阵的充分必要条件是A是非退化矩阵.

3，可逆矩阵的性质

补充:若矩阵A可逆则A的伴随矩阵也可逆
补充:若矩阵A可逆则A逆矩阵的行列式=A行列式的逆矩阵形式
补充:AA^-1=E,|A|乘|A|的逆矩阵形式=1

4，逆矩阵的求法

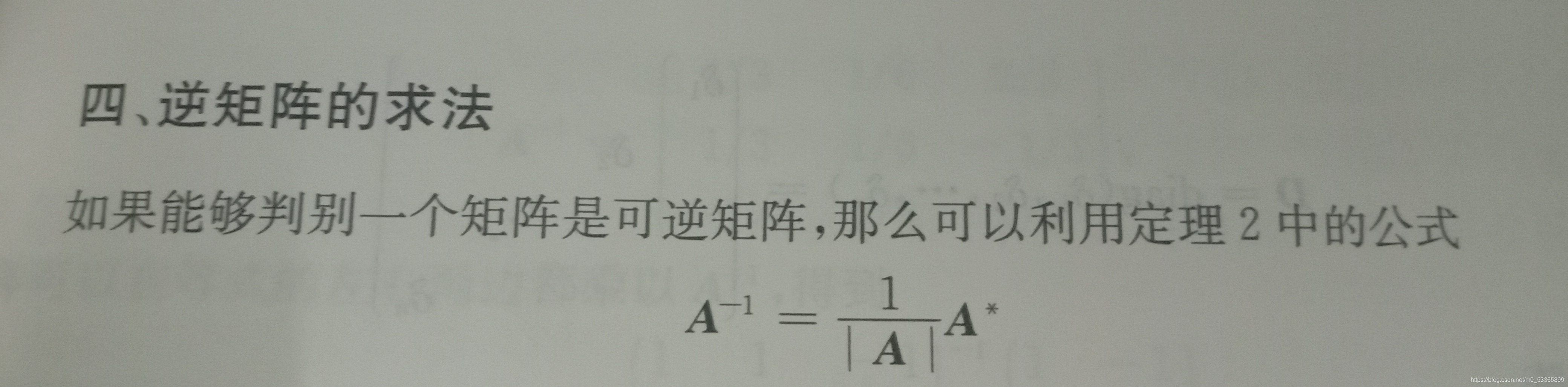
5，正交矩阵

设A是一个n阶方阵，如果A满足
AAᵀ=AᵀA=E
与逆矩阵的定义相比较，可以得出A^-1=Aᵀ

（四），矩阵的初等变换和初等矩阵

1，矩阵的初等变换和初等矩阵的定义

注意: 单位矩阵经过一次初等变换得到矩阵叫做初等矩阵

以下三种变换称为矩阵的初等变换

设A=(aij)是一个mxn矩阵则对A做一次初等行变换得到的矩阵等于在A的左边乘以相应的m阶行初等矩阵，对A做一次初等列变换得到的矩阵，等于在A的右边乘以相应的n阶列初等矩阵，具体说：

注意：左乘行变换，右乘列变换

推论：

（1）初等方阵均可逆
（2）初等方阵其逆矩阵也是初等方阵
（3）初等方阵的转置也是初等方阵

2，矩阵的初等变换和初等矩阵的应用

矩阵A经过有限次初等（或单独行、单独列）变换得到矩阵B，记作A(行或列)等价于B，记作 A ～B。

等价的性质:

1. 反射性 A和它本身等价

2. 对称性 A和B等价，则B和A是等价的

3. 传递性 A等于B B等价于C 则A等价于C

对于矩阵A,B mxn有以下结论
A行等价于B的充要条件是存在m阶的可逆矩阵P使得 PA=B (P左乘A等于B)
A列等价于B的充要条件是存在n阶的可逆矩阵Q使得 AQ=B (Q右乘A等于B)
A等价B的充要条件是存在m阶的可逆矩阵P和n阶的可逆矩阵Q使得PAQ=B

重点：初等变换法求逆矩阵

例如：
设A是一个n阶的可逆矩阵，则A经过一系列初等变换后可形成一个n阶的单位矩阵
P1P2P3P4P5…PnA=En
而P作为行初等矩阵也是初等矩阵，而初等矩阵均可逆所以
A^-1=P1P2P3P4…PnEn
可以将可逆矩阵A及单位矩阵En左右并排放在一起，组成一个nx2n矩阵（A,En）于是
P1P2P3…Pn(A,En)=(P1P2…PnA,P1P2…PnEn)=(En,A^-1)
(A,En)----->初等行变换(En,A^-1)

同理：
初等列变换也是如此

（五），分块矩阵

所谓分块矩阵就是把一个高阶矩阵看做是由一些低阶小矩阵组成的，在运行时这些小矩阵相当于元素，这些小矩阵称为高阶矩阵的子块
分块矩阵具体运算过程和普通矩阵几乎一样
例如：

（六），矩阵的秩

矩阵的秩 R(A)大于等于0小于等于min{m,n}。
r(A) = m 取了所有的行，叫行满秩
r(A) = n 取了所有的列，叫列满秩
r(A) < min{m,n}则叫做降秩
A是方阵，A满秩的充要条件是A是可逆的(转换为A的行列式不等于0，所以可逆)
r(A) = r的充要条件是有一个r阶子式不为0，所有r+1阶子式为0
矩阵A（m乘n阶）左乘m阶可逆矩阵P，右乘n阶可逆矩阵Q，或者左右乘可逆矩阵PAQ不改变其秩。
对矩阵实施(行、列）初等变换不改变矩阵的秩
阶梯形矩阵的秩 r(A)等于非零行的行数。
A的秩等于A转置的秩
任意矩阵乘可逆矩阵，秩不变