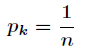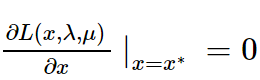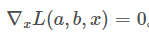本文不做数学推导，从物理意义上讲解拉格朗日乘子法。

原问题

我们要解决带有等式约束的最优化问题。为方便书写，以二维函数为例：
$$maxf(x,y),s.t.g(x,y)=0$$

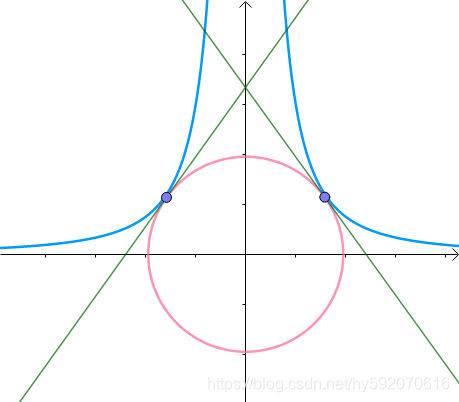
用下图表示这个问题。$f(x)$参数在二维平面内，其本身是一个曲面，用等高线（蓝色）表示。$g(x)=0$是二维平面内的一条曲线（红色）。

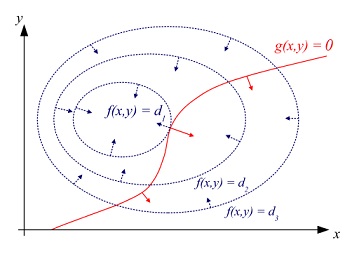
我们要找$g(x,y)=0$上的一个点，其位于$f(x,y)$最大的等高线上。

问题转换

Step 1

求解上述问题等价于：

找到$g(x,y)=0$上的一点，这一点处$g(x,y)=0$和该点$f(x,y)$的等高线相切。

可以用反例直观地理解。如果$g(x,y)=0$和该点$f(x,y)$等高线相交（黑点），如下图：

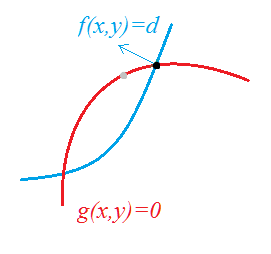
$g(x,y)=0$能够延伸到等高线$f(x,y)=d$更大的一侧。这个区域内的解（灰点），同样满足$g(x,y)=0$，但$f(x,y)$更大。

Step 2

更进一步，这一条件等价于：

找到$g(x,y)=0$上的一点，这一点$g(x,y)=0$和$f(x,y)=d$的梯度共线。

我们可以把这句话拆分成三个条件：

$$g(x,y)=0$$

$$\frac{\partial f(x,y)}{\partial x}=\lambda \frac{\partial g(x,y)}{\partial x}$$

$$\frac{\partial f(x,y)}{\partial y}=\lambda \frac{\partial g(x,y)}{\partial y}$$

三个方程，三个未知数，这样实际就可以求解了。

不过，为了记忆简洁，同时方便计算机运算，我们还可以把三式合为一式：

$$L(x,y,\lambda )=f(x,y)-\lambda g(x,y)$$

$$\nabla L(x,y,\lambda )=0$$

其中$\nabla$表示对三个参数求导。其中$\lambda$称为拉格朗日乘子，$L$称为拉格朗日函数。

求解

通过$\nabla L=0$可以求解出若干组参数，分别代入$f(x,y)$，找出值最大的一组，即为所求。