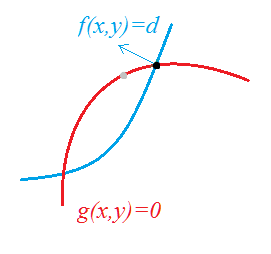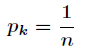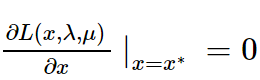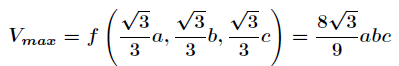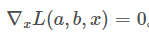参考
百度百科
拉格朗日乘数法：https://www.cnblogs.com/maybe2030/p/4946256.html
拉格朗日乘数法的一种几何解释：https://zhuanlan.zhihu.com/p/368334607
拉格朗日乘子法与KKT条件：https://zhuanlan.zhihu.com/p/392900101
Karush-Kuhn-Tucker (KKT)条件：https://zhuanlan.zhihu.com/p/38163970

一、简介

拉格朗日乘数法（Lagrange Multiplier）是以数学家拉格朗日命名的。约瑟夫·拉格朗日（Joseph-Louis Lagrange，1736~1813）全名为约瑟夫·路易斯·拉格朗日，法国著名数学家、物理学家。1736年1月25日生于意大利都灵，1813年4月10日卒于巴黎。他在数学、力学和天文学三个学科领域中都有历史性的贡献，其中尤以数学方面的成就最为突出。前辈尊容如下：

在数学最优问题中，拉格朗日乘数法是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。

二、拉格朗日乘数法

1、定义

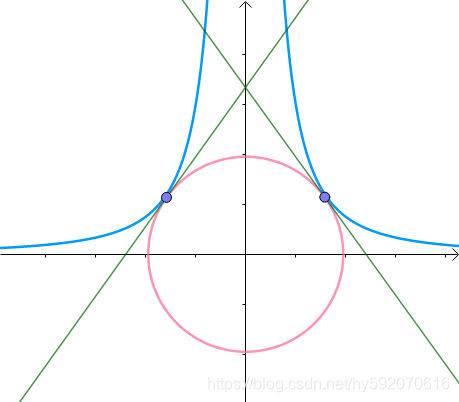
这个定义探讨的是二元函数，附加条件有一个，为了让原二元函数受到附加函数的限制，通过引入了了一个拉格朗日乘数因子，然后组建了一个新的函数，更其名曰拉格朗日函数。在拉格朗日函数中，不仅有原来的两个自变量x,y，还包含了另一个新的自变量拉格朗日乘数。拉格朗日函数对这三个自变量求偏导，令其偏导数为零，就可得极值点。若极值点只有一个的化，那么此点即为所求；否则需在多个极值点中在定义域的基础上寻得一个最值，最值即为所求。

2、算例

下面给出一个算例

大图：https://img-blog.csdnimg.cn/8d039c39b6f942dab133eef041cf19ca.png

上面给出的算例很简单，可以把约束条件代入到目标函数中，但是如果给出的进而形成新的目标函数，新的目标函数的极值即为所求。但是如果约束条件不被代入到目标函数中或者代起来相当复杂，比如此例若约束条件为 $x^3+y^3=5$，那么上述法一就不可使用或使用起来比较复杂，但是用拉格朗日乘数法依然步骤鲜明，计算简便。这就是拉格朗日乘数法的优势，这样看来拉格朗日乘数法就是更"一般"的方法。

三、广义拉格朗日乘数法

我们上述讨论的问题为等式约束优化问题，但等式约束并不足以描述人们面临的所有问题，不等式约束比等式约束更为常见，大部分实际问题的约束都是不超过多少时间，不超过多少人力，不超过多少成本等等。所以有些科学家拓展了拉格朗日乘数法，增加了KKT条件之后便可以用拉格朗日乘数法来求解不等式约束的优化问题了。笔者暂且用广义拉格朗日乘数法对这种方法进行命名。

1、KKT 条件的导出

上述结论可推广至多个约束等式与约束不等式的情况。考虑到标准约束优化问题（或称非线性规划）：

2、算例