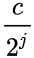ShuffleNet V1 概述
论文:ShuffleNet:An Extremely Efficient Convolutional Netural Network for Mobile Devices
ShuffleNet跟MobileNet一样也是一种轻量化网络,ShuffleNet V1.0版本中作者有提出Channel shuffle的概念。在ShuffleNet Block当中使用的基本上都是GConv 和DWConv


ShuffleNet v1 性能指标

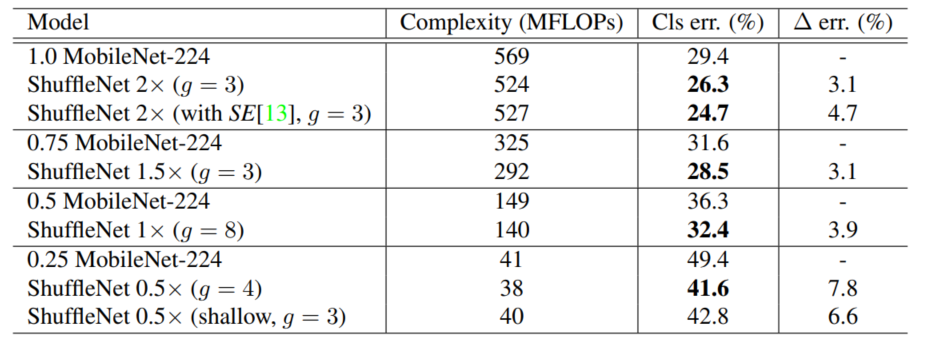
可以看出:
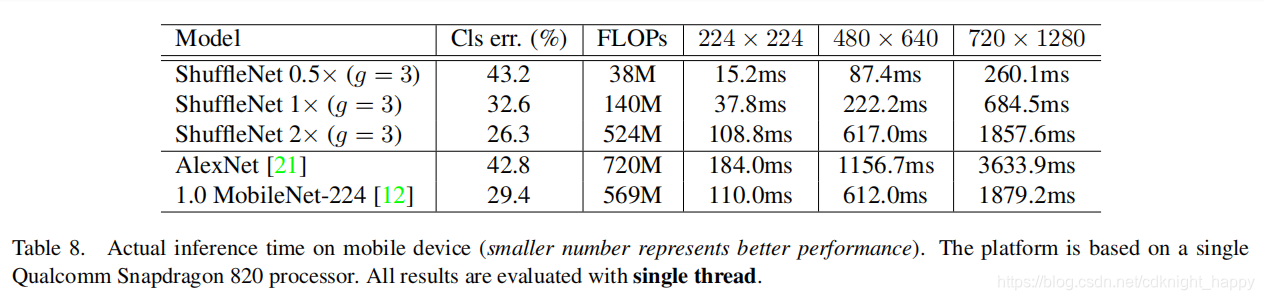
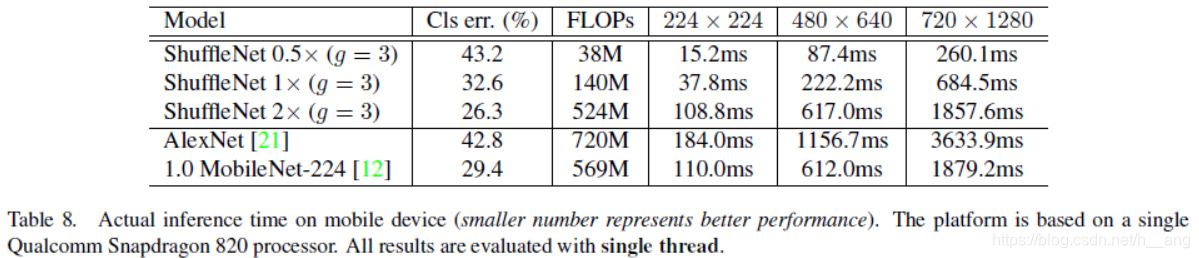
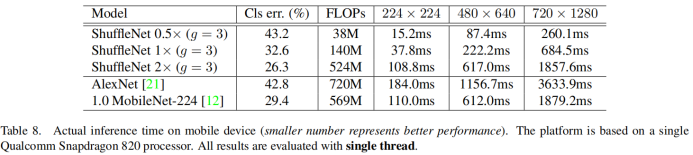
ShuffleNet0.5x的err率与我们AlexNet其实是差不多的(43.2% 42.8%)- 在晓龙820处理器上的推理时间是
15.2ms,而AlexNet需要184ms - ShuffleNet 1x 的
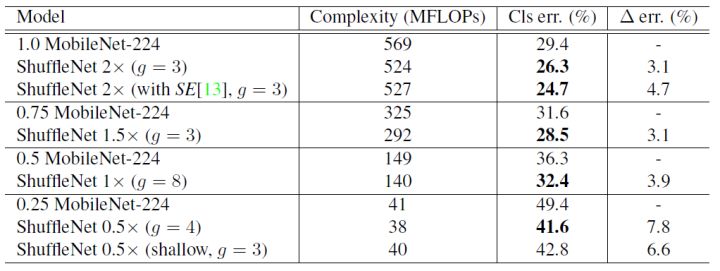
err率是32.6%,推理时间是37.8ms``;ShfuffleNet 2x的err率是26.3%,推理时间是108.8ms; 对比MobileNet 1.0它的err率是29.4,推理时间是110ms;可以看出ShuffleNet 2x的性能会比较好
Channel Shuffle
在ShuffleNet v1论文提出了Channel Shuffle这个概念

- 在这幅图中我们可以看到,对于我们的输入特征矩阵,通过串行的2个GConv
(Group Conv),对于普通的组卷积计算我们发现,它每次卷积都是针对该组内的一些channel的信息进行卷积操作。如果只是简单的串联的话,你会发现它一直都是针对同一个组内的channel数据进行处理,每个group之间是没有任何交流的,这样效果肯定就不好。 - 虽然采用
group conv能减少参数和运算量,如果只是直接对我们组卷积进行简单的堆叠你会发现。GConv中不同组之间的信息是没有交流的。
为了解决每个group之间是没有任何信息交流的问题,作者提出了channel shuffle的概念:
- 首先我们还是通过我们的输入
input,经过一个group conv得到它对应的特征矩阵。 - 假设如图,
Gconv划分了3个group,我们针对每个group生成的特征矩阵,在进一步划分对每个group划分了3个子group。我们将每个group当中的第一份给放到一起,将每个group的第二份也放到一起,每个group的第三份也放到一起。这样我们就得到了经过channel shuffle之后的特征矩阵了。
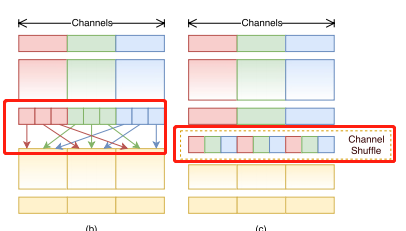
在使用经过channel shuffle之后的特征矩阵进行group卷积的话,这样它就以已经能够融合不同group之间的channel信息了。这就是channel shuffle思想。
用group卷积替换pw卷积
作者发现在ResNeXt中pw卷积占了93.4%的理论计算量,通过这个可以发现在网络上使用group卷积(对应ResNeXt中的DW卷积)占用的计算量是很小的,大部分都被1x1的普通卷积给占用了。

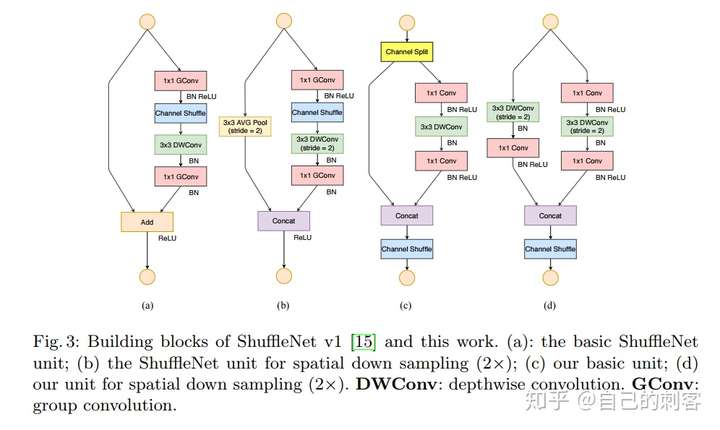
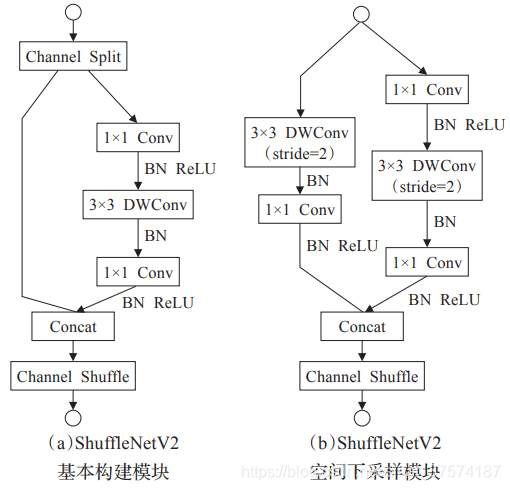
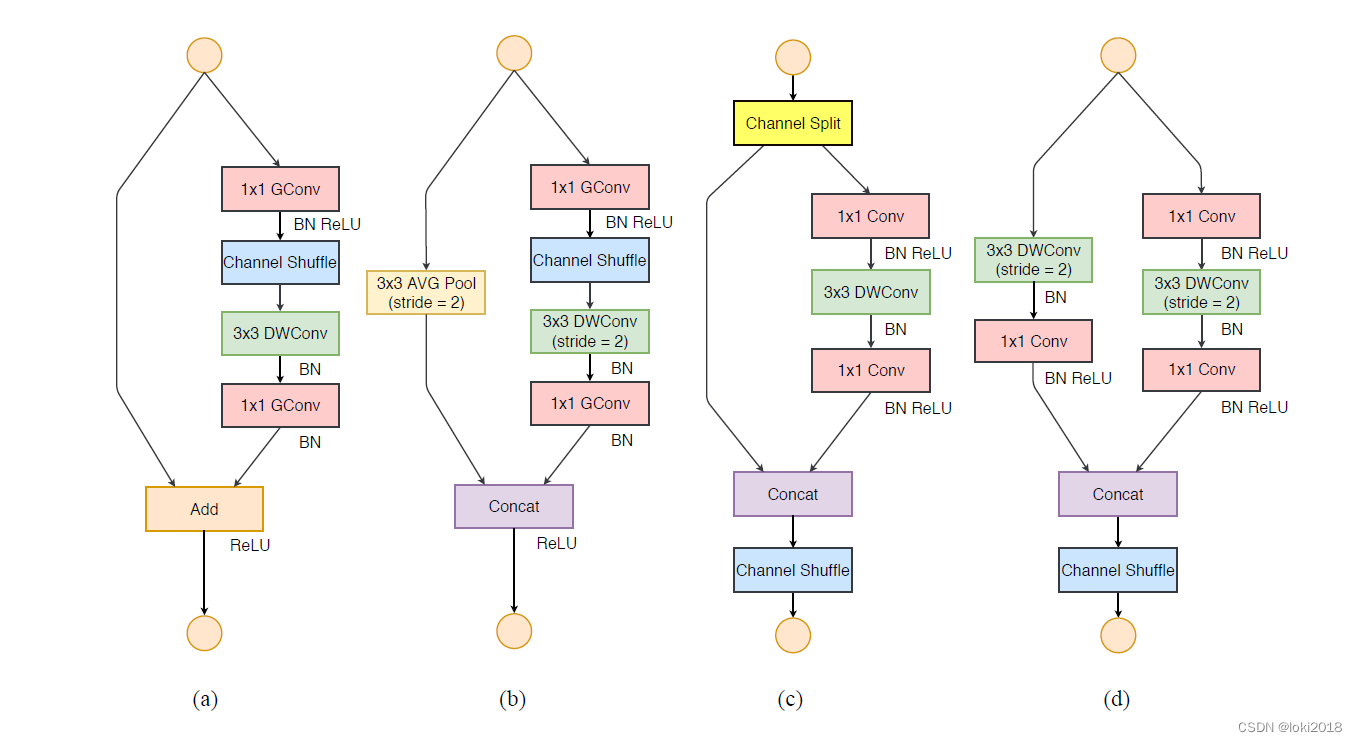
- 所以在shuffleNet1.0版本中,作者将(a)图中的
1x1卷积以及我们输出的1x1卷积,全全部都给换成了group卷积。

图 b它是针对strip=1的情况,左边捷径分支直接将输入引过来了。右边部分,首先通过1x1 的GConv以及BN和Relu,对得到的特征矩阵进行channel shuffle.然后通过一个3x3的DWConv以及BN,紧接着通过1x1的GConv,在通过BN,最后在与我们的输入特征矩阵进行相加的操作,通过Relu激活函数得到输出。图 c它是针对 shufflenet的strip=2的情况,在ResNet或者ResNeXt的网络当中,当strip=2的情况下我们在捷径分支上之前是直接通过一个卷积来进行下采样的,然后在shuffleNet网络中是通过池化层大小为3x3,步距为2的池化层进行下采样的。右边部分,首先通过1x1 的GConv以及BN和Relu,对得到的特征矩阵进行channel shuffle.然后通过一个3x3的DWConv这里的strip=2以及BN,紧接着通过1x1的GConv,在通过BN。需要注意最后是通过Concat拼接在一起的,并没有像图a,图b一样通过add方式进行相加。通过concat拼接,然后relu输出。
ShuffleNet V1网络搭建
下表是ShuffleNet v1中作者给出的一个表,这个表格中作者给出了如何搭建我们的shuffleNet,这里我们只需要看g=3这个版本就可以了。因为原论文很多实验,都是使用当g=3这个版本,g表示的是group数.

- 首先输入图片通过一个卷积核KSize为
3x3,步距stride为2,重复次数Repeat为1,输出channel为24个卷积核。然后接一个池化核为3x3,步距stride为2的MaxPool. - 然后接
Stage2、Stage3、Stage4,针对每个stage它就是将我们shuffleNet中的每个block进行堆叠。 - Stage2中第一个block,它的步距为2,重复次数为1,它的输出channel为240;然后在对我们步距为1的block堆叠3次,它的输出channel为240.对于后面的Stage3,Stage4 都是通过一样的方式堆叠。
- 经过stage 后,通过
grouppool平均池化以及全连接层得到我们最终的输出。这就是我们整个shuffleNet v1的框架。 - 对于
Stage2~Stage4,它的第一个block都是一个步距为2的block,也就是上图图c所对应的block,对于其他stride=1都是采用图b所示的block. - 对于下个stage,输出特征矩阵的channel会进行一个翻倍的操作,stage2到stage3我们能够看到特征矩阵的channel从240到翻到了480.再从480翻到了960,这就是原文所说的翻倍操作。
这里还需要注意一点,对于我们Stage 2,论文中说到对于我们第一个pw卷积(1x1)我们是不会使用GConv的,也就是对应图c的block,它的1x1卷积直接使用的是普通卷积没有用GConv,因为对于第一个pw它的input channel是非常小的,只有24.对于一个channel为24的特征矩阵。我们就没有必要使用GConv卷积了。对于其他的block都是使用GConv代替pw卷积
ShuffleNet V1轻量化
对比ResNet,ResNeXt,ShuffleNet的Flops,我们假设输入特征矩阵的channel为c, 高宽为h,w; 中间的bottleneck,这里指的是第一个1x1卷积和第2个DW卷积,它的输出channel为m,我们可以计算ResNet,ResNeXt,ShuffleNet的Flops:

R e s N e t : h w ( 1 ∗ 1 ∗ c ∗ m ) + h w ( 3 ∗ 3 ∗ m ∗ m ) + h w ( 1 ∗ 1 ∗ m ∗ c ) = h w ( 2 c m + 9 m 2 ) ResNet: hw(1*1*c*m) +hw(3*3*m*m) +hw(1*1*m*c) = hw(2cm+9m^2) ResNet:hw(1∗1∗c∗m)+hw(3∗3∗m∗m)+hw(1∗1∗m∗c)=hw(2cm+9m2)
R e s N e X t : h w ( 1 ∗ 1 ∗ c ∗ m ) + h w ( 3 ∗ 3 ∗ m ∗ m ) / g + h w ( 1 ∗ 1 ∗ m ∗ c ) = h w ( 2 c m + 9 m 2 / g ) ResNeXt: hw(1*1*c*m) +hw(3*3*m*m)/g +hw(1*1*m*c) = hw(2cm+9m^2/g) ResNeXt:hw(1∗1∗c∗m)+hw(3∗3∗m∗m)/g+hw(1∗1∗m∗c)=hw(2cm+9m2/g)
S h u f f l e N e t : h w ( 1 ∗ 1 ∗ c ∗ m ) / g + h w ( 3 ∗ 3 ∗ m ) + h w ( 1 ∗ 1 ∗ m ∗ c ) / g = h w ( 2 c m / g + 9 m ) ShuffleNet: hw(1*1*c*m) /g+hw(3*3*m) +hw(1*1*m*c)/g = hw(2cm/g+9m) ShuffleNet:hw(1∗1∗c∗m)/g+hw(3∗3∗m)+hw(1∗1∗m∗c)/g=hw(2cm/g+9m)
ResNeXt的block与ResNet的区别是首先接一个1x1的卷积,然后接一个GConv卷积,最后接一个1x1卷积,因为GConv卷积的参数是一般卷积参数的 1 / g 1/g 1/g,所以ResNeXt第二项表达式为: h w ( 3 ∗ 3 ∗ m ∗ m ) / g hw(3*3*m*m)/g hw(3∗3∗m∗m)/gShuffleNet v1,第一个1x1的GConv,第二个为3x3的GConv,第三个为1x1的GConv;第一个GConv的计算量为普通卷积的 1 / g 1/g 1/g,同理最后一个1x1的GConv的计算量为普通卷积的 1 / g 1/g 1/g;对于中间的DW卷积就是我们GConv的特殊情况,当我们的g=m的时候,当g=m时就约去了一个m,所以就有 h w ( 3 ∗ 3 ∗ m ) hw(3 * 3 *m) hw(3∗3∗m)
通过这3个对比,我们就知道ShuffleNet的Flops是最小的。
总结
ShuffleNet v1网络的主要思想是:
- 我们在
GConv加上了一个channel shuffle模块 - 对于block而言,将其中两个
1x1卷积全部替换成GConv