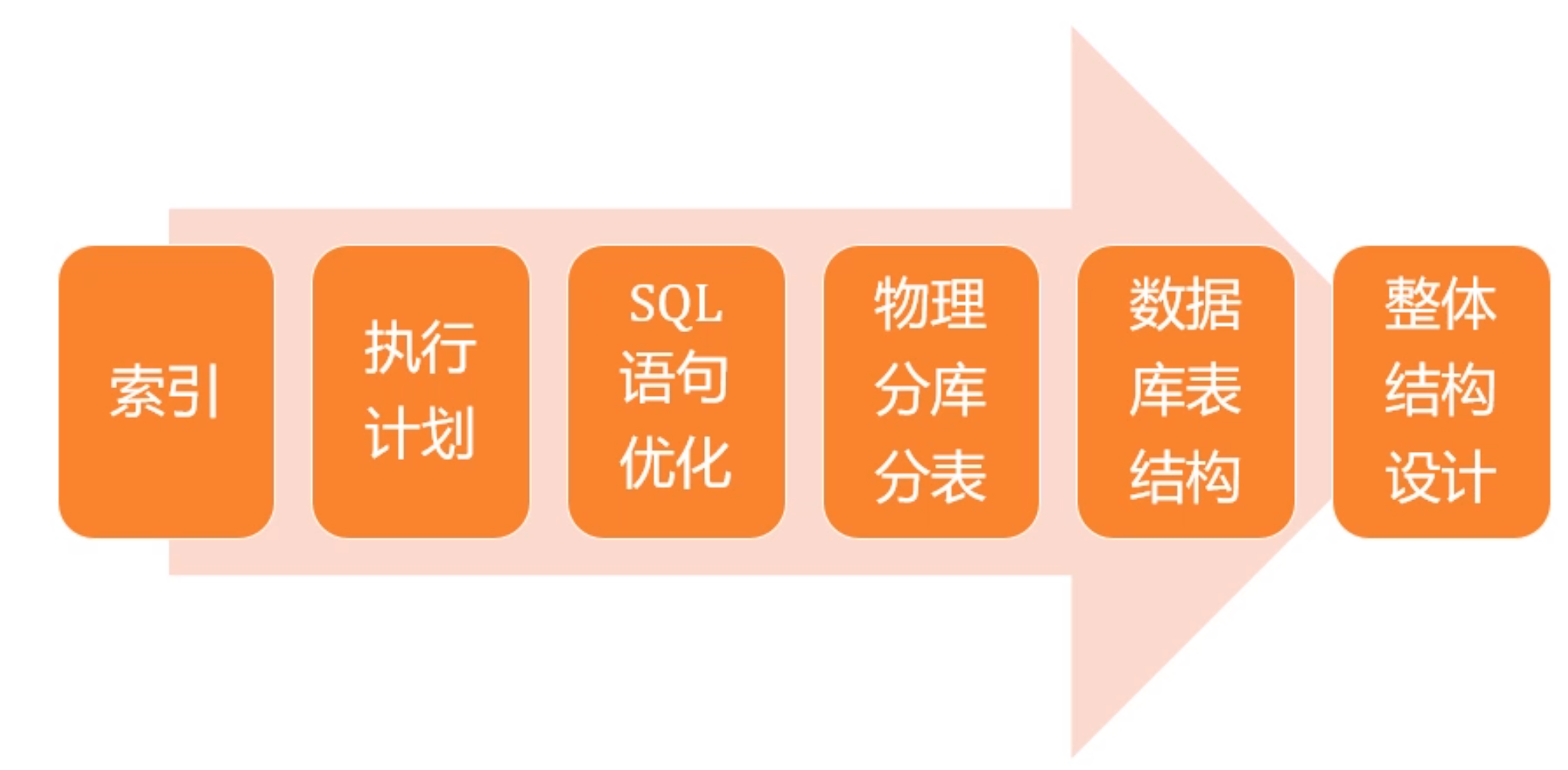
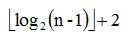线段树是我接触到的第一个高级数据结构,也是我接触过的模板最长的一种代码,但他的实用性真的很强,绝大部分的区间问题都可以用线段树解决点,所以今天我打算简单介绍一下我对线段树的理解
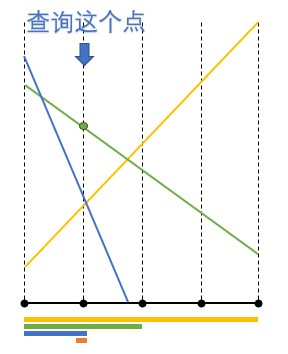
先放一张百度来的线段树图片:

线段树大概就长这个样子,我们可以清楚的看到,在树的每一层中,所有的区间和恰好就是整个区间,而且同一层中的不同区间不会存在交集。
先来说一下线段树可以进行的操作,可以区间修改,区间查询,单点修改,单点查询,复杂度都是(logn),这时候可能就会问了,我们通过数组进行单点修改和单点查询复杂度是o(1),为什么还要学复杂度更高的呢?这时候又会有同学说了,涉及到区间修改和查询的可以用前缀和和差分啊?但是需要注意的是前缀和和差分主要针对的是静态的,而不是动态的区间值问题. 虽然用数组单点修改和单点查询复杂度比较低,但是区间修改和区间查询复杂度都是o(n),所以总体来说复杂度就是o(n).
下面说一下线段树的几个具体操作:
看这个图有没有一种二分的感觉?其实线段树的基本思想就是二分。
我习惯是用数组实现线段树,一般需要维护4个数组
l[id]:标号为id的区间的左边界
r[id];标号为id的区间的右边界
sum[id]:标号为id的区间的所有数的和(根据题目不同,这个数组具有不同的含义)
lazy[id]:标号为id的区间的子区间需要进行的更新操作
建树代码:
void build(int id,int L,int R)
{//建树时要在一开始就初始化 l[id]=L,r[id]=R,sum[id]=0,lazy[id]=0;if(L==R){sum[id]=a[L];return ;}int mid=L+R>>1;//递归建立两个子节点 build(id<<1,L,mid);build(id<<1|1,mid+1,R);pushup(id);//用子节点更新父节点
}我们在建树时一开始是先递归到叶子节点再对父亲节点进行更新的,在回溯过程中我们需要进行更新操作,更新方式根据题意的不同而不同,以总和为例,更新代码:
//只有区间修改和点的修改才会加pushup操作
//id代表当前区间的编号
void pushup(int id)
{//这里不一定是求和,还可以是其他具有共性的性质,比如最大值最小值公约数等等 sum[id]=sum[id<<1]+sum[id<<1|1];
}接下来是单点更新操作,就是先递归找到这个点,然后进行更新,在回溯过程中对父节点更新一下就好,代码:
void update_point(int x,int id,int val)
{if(l[id]==r[id]){sum[id]=val;return ;}int mid=l[id]+r[id]>>1;pushdown(id);//题目中若无区间更新操作,则无需添加 if(x<=mid) update_point(x,id<<1,val);else update_point(x,id<<1|1,val);pushup(id);
}单点查询操作与单点更新操作极其相似,也是先递归找到这个点,然后返回这个点的值就行了,与单点更新就差一个pushup操作,代码:
void query_point(int x,int id)
{if(l[id]==r[id]) return sum[id];int mid=l[id]+r[id]>>1;pushdown(id);//判断查询节点属于哪棵子树中 if(x<=mid) query_point(x,id<<1);else query_point(x,id<<1|1);
}接下来就是区间更新操作了,区间更新操作与单点更新操作不同,并不是一定要递归到所需更新区间的每个点进行更新,而是直接对其子区间的sum数组进行更新,并打上懒标记,如果需要用到其子区间的sum,需要先更新再使用,这也就是懒标记的作用.下面是pushdown操作代码:
//涉及到区间修改的题目一般都需要加pushdown操作,也因此需要加lazy数组
void pushdown(int id)
{if(lazy[id]){//用父节点的lazy数组去更新子节点的lazy数组 lazy[id<<1]+=lazy[id];lazy[id<<1|1]+=lazy[id];//子节点的sum要加父节点的lazy标记乘以子节点对应区间的长度 sum[id<<1]+=(r[id<<1]-l[id<<1]+1)*lazy[id];sum[id<<1|1]+=(r[id<<1|1]-l[id<<1|1]+1)*lazy[id];lazy[id]=0;//千万不要忘记清空父节点的lazy数组 }
}区间修改就是先递归找到目标区间的子区间,然后对其sum数组进行操作,并打上懒标记,注意找子区间前一定要进行pushdown操作,防止子区间需更新但还未更新,导致使用错误的sum数组的值.,在回溯的时候要进行pushup操作,对其父节点进行更新,下面是代码:
//区间修改中的L,R代表目标区间的左右边界
void update_interval(int id,int L,int R,int val)
{//当前区间不在目标区间中,直接返回 if(l[id]>R||r[id]<L) return ;//当前区间是目标区间的子集,直接进行更新,做上lazy标记后就无需递归子节点 if(l[id]>=L&&r[id]<=R){sum[id]+=val*(r[id]-l[id]+1);lazy[id]+=val;return ;}//千万别忘记pushdown操作,有可能之前做过lazy标记但还未更新 pushdown(id);//递归两个子节点 update_interval(id<<1,L,R,val);update_interval(id<<1|1,L,R,val);pushup(id);
}区间查询操作比较简单,准确来说就是把目标区间分成若干个已经划分好的区间,这些区间都是无交集的,但这些区间并不一定在树的同一层,我们只需要返回这些区间的sum值即可,代码:
int query_interval(int id,int L,int R)
{if(l[id]>R||r[id]<L) return 0;if(l[id]>=L&&r[id]<=R) return sum[id];pushdown(id);return query_interval(id<<1,L,R)+query_interval(id<<1|1,L,R);
}上面就是线段树的基本代码了,大家可以按照我一开始放置的百度图片进行理解,线段树模板比较长,有时候也需要灵活转变,所以一定要深刻理解他的本质,在接下来的博客中我会放一些线段树的题目,如果大家有什么好的线段树题目,欢迎在评论区里面分享!