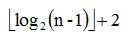目录:
线段树基本常识
线段树的的存储
线段树的基本操作
1. 建树
2. 单点查询
3. 单点修改
4. 区间查询
5. 区间修改
例题推荐:
线段树 1
线段树 2
线段树基本常识
线段树是一种二叉搜索树(即每个节点最多有两颗子树),与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
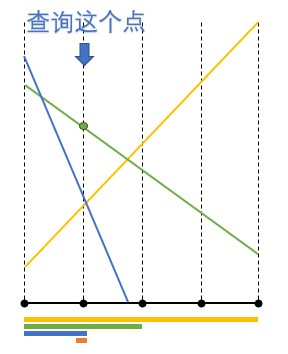
如下图,就是一颗 [1,10] 的线段树的分解过程:

由图可得出一个结论,线段树的最大深度不超过 ,且每一颗线段树需要 4*n 的辅助空间,如果没有开到 4*n ,那就完美 RE 了!!!
线段树的的存储
线段树采用的是堆式储存法,即编号为 k 的节点的做儿子为 k*2、右儿子为 k*2+1、父亲节点为k/2;二进制运算优化就是 k<<1,k<<1|1,k>>1。
通常来说,每个节点会存储:区间左边界、区间右边界、答案及其有关信息。
线段树的基本操作
1. 建树
采用递归遍历整棵树,每次将区间分为左右两个区间,对与叶子接点直接赋值,非叶子节点由左右子树合并。
inline void build(int k,int l,int r)//k为当前节点,[l,r]为当前区间
{ if(l==r)//到达叶子节点,记录节点信息{sum[k]=a[l];return;//记得返回}int mid=(l+r)>>1;build(k*2,l,mid);//左右分别建树build(k*2+1,mid+1,r);sum[k]=sum[k*2]+sum[k*2+1];//合并区间信息return;
}2. 单点查询
采用类似二分的思想,将现区间 [ l,r ] 分为左右两个区间 [ l,mid ]、[ mid+1,r ] ,判断查找的位置 x 是在左区间还是在右区间,继续递归,如到达叶子节点,则直接返回节点信息。
inline int find(int k,int l,int r,int x)//k为当前节点位置,[l,r]为当前区间,x为目标节点
{if(l==r) return sum[k];//找到目标节点,返回节点信息int mid=(l+r)>>1;if(x<=mid) return find(k*2,l,mid,x);//查询位置在左子树else return find(k*2+1,mid+1,r,x);//查询位置在右子树
} 3. 单点修改
类似于单点查询,找到目标位置,直接进行修改,最后合并区间信息
inline void change(int k,int l,int r,int x)//k为当前节点位置,[l,r]为当前区间,x为目标节点
{if(l==r)//找到目标节点,进行修改{sum[k]+=x;//这里是区间累加return;}int mid=(l+r)>>1;if(x<=mid) change(k*2,l,mid,x);//所查询位置在左子树else change(k*2+1,mid+1,r,x);//所查询位置在右子树sum[k]=sum[k*2]+sum[k*2+1];//合并区间信息return;
}4. 区间查询
目标区间 [ x,y ] ,当前区间 [ l ,r ] ,如果当前区间被目标区间包含,则直接返回区间信息,否则按照将当前区间分为左右两个区间进行查找的思想继续递归查询,最后所有返回区间的并集就是目标区间的答案。
inline int find(int k,int l,int r,int x,int y)//k为当前节点位置,[l,r]为当前区间,[x,y]为目标区间
{if(x<=l&&r<=y) return sum[k];//当前区间被目标区间所包含,直接返回区间信息int mid=(l+r)>>1;int res=0;//用于左右子树区间值的累加if(x<=mid) res+=find(k*2,l,mid,x,y);//查询左子树if(y>mid) res+=find(k*2+1,mid+1,r,x,y);//查询右子树return res;//返回值
}5. 区间修改
如单点查询和单点修改一样,区间修改也是区间查询的一个延续,但不同的是,若修改区间内全部的节点信息,复杂度将会非常大,你也会迎来线段树的第一个 TLE ,于是,便有大佬按耐不住了,给我们引入了 “ 懒标记 ” 这一神奇函数。
懒标记:若遍历到带有懒标记的节点,则立刻修改当前节点的值,并将标记下放到左右子树(这一过程被称为:标记下放),但左右子树的信息不发生改变,只有去遍历左右子树的时候,才修改其信息。
懒标记大大提高了程序的运行效率,其核心思想就是:只修改对查询有用的节点。
inline void Add(int k,int l,int r,int v)//修改区间值
{add[k]+=v;//懒标记也要加vsum[k]+=v*(r-l+1);//区间值等于原值加上区间内数的个数乘上修改值return;
}
inline void pushdown(int k,int l,int r)//标记下方
{if(!add[k]) return;//判断是否带有懒标记int mid=(l+r)>>1;Add(k*2,l,mid,add[k]);//左子树修改同时下方标记Add(k*2+1,mid+1,r,add[k]);//右子树修改同时下方标记add[k]=0;//标记清空return;
}
inline int find(int k,int l,int r,int x,int y)//带懒标记的区间查询
{if(x<=l&&r<=y) return sum[k];int mid=(l+r)>>1;int res=0;pushdown(k,l,r);if(x<=mid) res+=find(k*2,l,mid,x,y);if(y>mid) res+=find(k*2+1,mid+1,r,x,y);return res;
}
inline void change(int k,int l,int r,int x,int y,int v)//k为当前节点位置,[l,r]为当前区间,[x,y]为目标区间
{if(x<=l&&r<=y)//当前区间被包含于目标区间{Add(k,l,r,v);//修改区间值return;}pushdown(k,l,r);//标记下方int mid=(l+r)>>1;if(x<=mid) change(k*2,l,mid,x,y,v);//左子树修改if(y>mid) change(k*2+1,mid+1,r,x,y,v);//右子树修改sum[k]=sum[k*2]+sum[k*2+1];//合并区间信息return;
}奉上完整代码(无注释):
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{int num=0,w=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();}while(ch>='0'&&ch<='9') {num=(num<<1)+(num<<3)+ch-'0';ch=getchar();}return num*w;
}
int n;
int a[4000001];
int sum[4000001];
int add[4000001];
inline void build(int k,int l,int r)
{ if(l==r){sum[k]=a[l];return;}int mid=(l+r)>>1;build(k*2,l,mid);build(k*2+1,mid+1,r);sum[k]=sum[k*2]+sum[k*2+1];return;
}
inline int find_spot(int k,int l,int r,int x)
{if(l==r) return sum[k];int mid=(l+r)>>1;if(x<=mid) return find_spot(k*2,l,mid,x);else return find_spot(k*2+1,mid+1,r,x);
}
inline void change_spot(int k,int l,int r,int x)
{if(l==r) {sum[k]+=x;return;}int mid=(l+r)>>1;if(x<=mid) change_spot(k*2,l,mid,x);else change_spot(k*2+1,mid+1,r,x);sum[k]=sum[k*2]+sum[k*2+1];return;
}
inline void Add(int k,int l,int r,int v)
{add[k]+=v;sum[k]+=v*(r-l+1);return;
}
inline void pushdown(int k,int l,int r)
{if(!add[k]) return;int mid=(l+r)>>1;Add(k*2,l,mid,add[k]);Add(k*2+1,mid+1,r,add[k]);add[k]=0;return;
}
inline int find_section(int k,int l,int r,int x,int y)
{if(x<=l&&r<=y) return sum[k];int mid=(l+r)>>1;int res=0;pushdown(k,l,r);if(x<=mid) res+=find_section(k*2,l,mid,x,y);if(y>mid) res+=find_section(k*2+1,mid+1,r,x,y);return res;
}
inline void change_section(int k,int l,int r,int x,int y,int v)
{if(x<=l&&r<=y){Add(k,l,r,v);return;}pushdown(k,l,r);int mid=(l+r)>>1;if(x<=mid) change_section(k*2,l,mid,x,y,v);if(y>mid) change_section(k*2+1,mid+1,r,x,y,v);sum[k]=sum[k*2]+sum[k*2+1];return;
}
int main()
{//freopen(".in","r",stdin);//freopen(".out","w",stdout);//一些奇奇怪怪的初始化、读入、输出、离散化…… //fclose(stdin);//fclose(stdout); return 0;
}例题推荐:
P3372 【模板】线段树 1
P3373 【模板】线段树 2
线段树 1
模板题,区间修改 + 区间查询 即可完美解决:
【代码实现】
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
int n,q,k,a,b,w,add[4000010],s[1000010];
long long sum[4000010];
void Add(int k,int l,int r,int v)
{add[k]+=v;sum[k]+=(long long)(r-l+1)*(long long)v;
}
void down(int k,int l,int r,int mid)
{if(!add[k])return;Add(k*2,l,mid,add[k]);Add(k*2+1,mid+1,r,add[k]);add[k]=0;
}
void change(int k,int l,int r,int x,int y,int v)
{if(l>=x&&r<=y){Add(k,l,r,v);return;}int mid=(l+r)/2;down(k,l,r,mid);if(x<=mid){change(k*2,l,mid,x,y,v);}if(y>mid){change(k*2+1,mid+1,r,x,y,v);}sum[k]=sum[k*2]+sum[k*2+1];
}long long query(int k,int l,int r,int x,int y,int v)
{if(l>=x&&r<=y){return sum[k];} int mid=(l+r)/2;long long res=0;down(k,l,r,mid);if(x<=mid){res+=query(k*2,l,mid,x,y,v);}if(y>mid){res+=query(k*2+1,mid+1,r,x,y,v);}return res;
}void build(int k,int l,int r)
{if(l==r){sum[k]=s[l];return;}int mid=(l+r)/2;build(k*2,l,mid);build(k*2+1,mid+1,r);sum[k]=sum[k*2]+sum[k*2+1];
}
int main()
{scanf("%d%d",&n,&q);for(int i=1;i<=n;i++){scanf("%d",&s[i]);}build(1,1,n);for(int i=1;i<=q;i++){scanf("%d",&k);if(k==1){scanf("%d%d%d",&a,&b,&w);change(1,1,n,a,b,w);}if(k==2){scanf("%d%d",&a,&b);printf("%lld\n",query(1,1,n,a,b,w));}}return 0;
}
线段树 2
在 区间修改 + 区间查询的基础上,对懒标记进行亿点点的改动即可:
【代码实现】
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int n,p,m;
long long a[500001];
struct node
{long long sum;long long mul;//*long long pule;//+
}tree[500001];
int add(int k)
{tree[k].sum=tree[k*2].sum+tree[k*2+1].sum;tree[k].sum%=p;
}
void gs(int k,int l,int r)
{int k1=k*2;int k2=k*2+1;int mid=(l+r)/2;tree[k1].sum*=tree[k].mul;tree[k1].sum%=p;tree[k1].sum+=tree[k].pule*(mid-l+1);tree[k1].sum%=p;tree[k2].sum*=tree[k].mul;tree[k2].sum%=p;tree[k2].sum+=tree[k].pule*(r-mid);tree[k2].sum%=p;tree[k1].mul*=tree[k].mul;tree[k1].mul%=p;tree[k2].mul*=tree[k].mul;tree[k2].mul%=p;tree[k1].pule*=tree[k].mul;tree[k1].pule%=p;tree[k1].pule+=tree[k].pule;tree[k1].pule%=p;tree[k2].pule*=tree[k].mul;tree[k2].pule%=p;tree[k2].pule+=tree[k].pule;tree[k2].pule%=p;tree[k].pule=0;tree[k].mul=1;return;
}
void build(int k,int l,int r)
{tree[k].pule=0;tree[k].mul=1;if(l==r){tree[k].sum=a[l];return;}int mid=(l+r)/2;build(k*2,l,mid);build(k*2+1,mid+1,r);add(k);
}
void change_pule(int k,int l,int r,int x,int y,long long w)
{if(y<l||x>r){return;}if(x<=l&&r<=y){tree[k].pule+=w;tree[k].pule%=p;tree[k].sum+=w*(r-l+1);tree[k].sum%=p;return;}int mid=(l+r)/2;gs(k,l,r);change_pule(k*2,l,mid,x,y,w);change_pule(k*2+1,mid+1,r,x,y,w);add(k);
}
void change_mul(int k,int l,int r,int x,int y,long long w)
{if(y<l||x>r){return;}if(x<=l&&r<=y){tree[k].sum*=w;tree[k].sum%=p;tree[k].mul*=w;tree[k].mul%=p;tree[k].pule*=w;tree[k].pule%=p;return;}int mid=(l+r)/2;gs(k,l,r);change_mul(k*2,l,mid,x,y,w);change_mul(k*2+1,mid+1,r,x,y,w);add(k);
}
long long find(int k,int l,int r,int x,int y)
{if(x>r||y<l){return 0;}if(x<=l&&r<=y){return tree[k].sum;}int mid=(l+r)/2;gs(k,l,r);long long r1,r2;r1=find(k*2,l,mid,x,y);r2=find(k*2+1,mid+1,r,x,y);return (r1+r2)%p;
}
int main()
{scanf("%d%d%d",&n,&m,&p);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}build(1,1,n);for(int i=1;i<=m;i++){int k;scanf("%d",&k);if(k==1){int t,g;long long c;scanf("%d%d%lld",&t,&g,&c);change_mul(1,1,n,t,g,c);}if(k==2){int t,g;long long c;scanf("%d%d%lld",&t,&g,&c);change_pule(1,1,n,t,g,c);}if(k==3){int t,g;scanf("%d%d",&t,&g);printf("%lld\n",find(1,1,n,t,g));}}return 0;
}