一，什么是线段树？

线段树是怎样的树形结构?

　　线段树是一种二叉搜索树，而二叉搜索树，首先满足二叉树，即每个结点最多有两颗子树，并且是一颗搜索树，我们要知道，线段树的每个结点都存储了一个区间，也可以理解成一个线段，而搜索，就是在这些线段上进行搜索操作得到你想要的答案。

线段树能够解决什么样的问题？

　　线段树的适用范围很广，可以在线维护修改以及查询区间上的最值，求和。对于线段树来说，每次更新以及查询的时间复杂度为O(logN)。

线段树和其他RMQ算法的区别

　　常用的解决RMQ问题有ST算法，二者预处理时间都是O(NlogN)

(详见ST算法解决BMQ问题详解)，而且ST算法的单次查询操作是O(1)，看起来比线段树好多了，但二者的区别在于线段树支持在线更新值，而ST算法不支持在线操作。

1. 静态的区间询问：ST表

2. 动态的区间询问：线段树/树状数组

静态指的是，数字不会发生改变
动态指的是，在查询过程中，数字可能会发生一定程度的修改

二,线段树的基本操作

建树

思路

首先，我们得先明白几件事情:

　每个结点存什么

结点下标是什么

如何建树

下面我以一个简单的求一段区间的最大值来描述上面的三个概念。

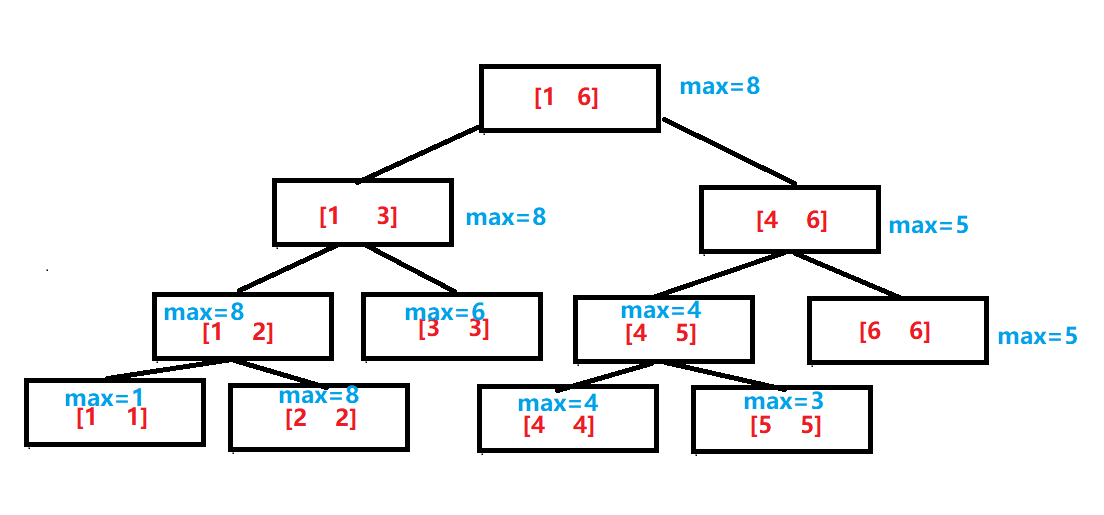
　　对于a[1~6] = {1,8,6,4,3,5}来说，线段树如上所示，红色代表每个结点存储的区间，蓝色代表该区间最值。

　　可以发现，每个叶子结点的值就是数组的值，每个非叶子结点的度都为二，且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。

　　那么结点到底是如何存储区间的呢，以及如何快速找到非叶子结点的孩子以及非根节点的父亲呢，这里也就是理解线段树的重点以及难点所在，线段树你只要理解了结点与结点之间的关系便能很快理解线段树的基本知识。

　　对于一个区间[l,r]来说，最重要的数据当然就是区间的左右端点l和r，但是大部分的情况我们并不会去存储这两个数值，而是通过递归的传参方式进行传递。这种方式可以直接用数组存树，那这里怎么快速使用下标找到左右子树呢?

　　对于上述线段树，我们增加绿色数字为每个结点的下标

　　则每个结点下标如上所示，这里你可能会问，为什么最下一排的下标直接从9跳到了12，因为中间其实是有两个空间的呀！！

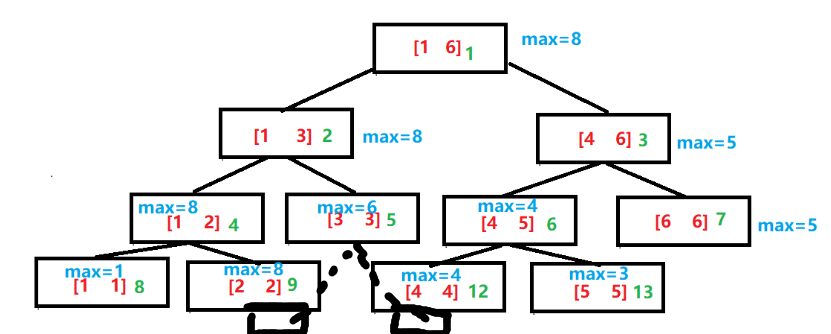
虽然没有使用，但是他已经开了两个空间，这也是为什么线段树建树需要2*2k（2k-1 < n < 2k)空间，一般会开到4*n的空间防止RE。

　　仔细观察每个父节点和子节点下标的关系，不难发现以下规律

l = fa*2 （左子树下标为父节点下标的两倍）
r = fa*2+1（右子树下标为父节点下标的两倍+1）

那么明白了数组如何存线段树,结点间的关系,

建树时每次递归就要先判断l是否等于r,等于就说明是叶子节点,也就是区间是[l,l],直接赋值成a[l]/a[r]，再返回。

否则就递归构造左儿子结点和递归构造右儿子结点,最后更新父节点。

是不是觉得其实很简单。

详细代码

void bui(int id,int l,int r)//创建线段树,id表示存储下标,区间[L,r]
{if(l == r)//左端点等于右端点，即为叶子节点(区间长度为1)，直接赋值即可{tr[id] = a[l];return ;}
// 否则将当前区间中间拆开成两个区间int mid = (l + r) / 2;//mid则为中间点，左儿子的结点区间为[l,mid],右儿子的结点区间为[mid + 1,r]bui(id * 2,l,mid); //递归构造左儿子结点bui(id * 2 + 1,mid + 1,r); //递归构造右儿子结点
// 左右两个区间计算完成以后
// 合并到当前区间tr[id] = min(tr[id * 2],tr[id * 2 + 1]);//更新父节点
}

看完代码是不是很清晰，这里也建议自己再次手动实现一遍理解递归的思路。

区间查询

思路

我们知道线段树的每个结点存储的都是一段区间的信息，如果我们刚好要查询这个区间，那么则直接返回这个结点的信息即可，比如对于上面线段树，如果我直接查询[1,6]这个区间的最值，那么直接返回根节点信息返回13即可，但是一般我们不会凑巧刚好查询那些区间，比如现在我要查询[2,5]区间的最值，这时候该怎么办呢，我们来看看哪些区间被[2,5]包含了。

　　一共有5个区间，而且我们可以发现[4,5]这个区间已经包含了两个子树的信息([4,4],[5,5])，所以我们需要查询的区间只有三个，分别是[2,2],[3,3],[4,5]，到这里你能通过更新的思路想出来查询的思路吗? 我们还是从根节点开始往下递归，如果当前结点是被要查询的区间包含了的，则返回这个结点的信息，这样从根节点往下递归，时间复杂度也是O(logN)。

详细代码

//id 表示树节点编号，l r 表示这个节点所对应的区间
//x y表示查询的区间
int find(int id,int l,int r,int x,int y)
{//需要查询的区间[x,y]将当前区间[l,r]包含的时候if(x <= l && r <= y) return tr[id];int mid = (l + r) / 2,ans = -INT_MAX;// 如果需要查询左半区间if(x <= mid) ans = min(ans,find(id * 2,l,mid,x,y));   // 如果需要查询右半区间if(y > mid) ans = min(ans,find(id * 2 + 1,mid + 1,r,x,y));return ans;
}

　　如果你能理解建树的过程，那么这里的区间查询也不会太难理解。还是建议再次手动实现。

单点更新

思路

很简单,就是从根节点递归去找a[x],找到了就返回,并再返回的一路上不断更新其父节点的max值。

详细代码

// id 表示树节点编号，l r 表示这个节点所对应的区间
// 将 a[x] 修改为 v
// 线段树单点更新
void gexi(int id, int l, int r, int x, int v)
{
// 找到长度为 1 的区间才返回if (l == r){tr[id] = v;return;}
//否则找到 x 在左区间或者右区间去更新int mid = (l + r) / 2;if (x <= mid) gexi(id * 2, l, mid, x, v);// 需要修改的值在左区间else gexi(id * 2 + 1, mid + 1, r, x, v);// 需要修改的值在右区间tr[id] = max(tr[id * 2], tr[id * 2 + 1]);
}

区间更新

意思

在线段树中会遇到区间更新的情况，例如在区间求和问题中，令[a,b]区间内的值全部加c，若此时再采用单点更新的方法，就会耗费大量时间，这个时候就要用到懒标记(lazy标记)来进行区间更新了。

建树

这个操作根普通的一模一样

思路(更新)

懒标记（lazy-tag），又叫做延迟标记。

设当前结点对应区间[l, r]，待更新区间[a, b]

　当 a ≤ l ≤ r ≤ b，即 [l, r]∈[a,b]时，不再向下更新，仅更新当前结点，并在该结点加上懒标记，当必须得更新/查询该结点的左右子结点时，再利用懒标记的记录向下更新（pushdown)——懒标记也要向下传递，然后移除该结点的懒标记。

这样就不用每次都更新到叶子结点，减少了大量非必要操作，从而优化时间复杂度。

具体举个栗子:

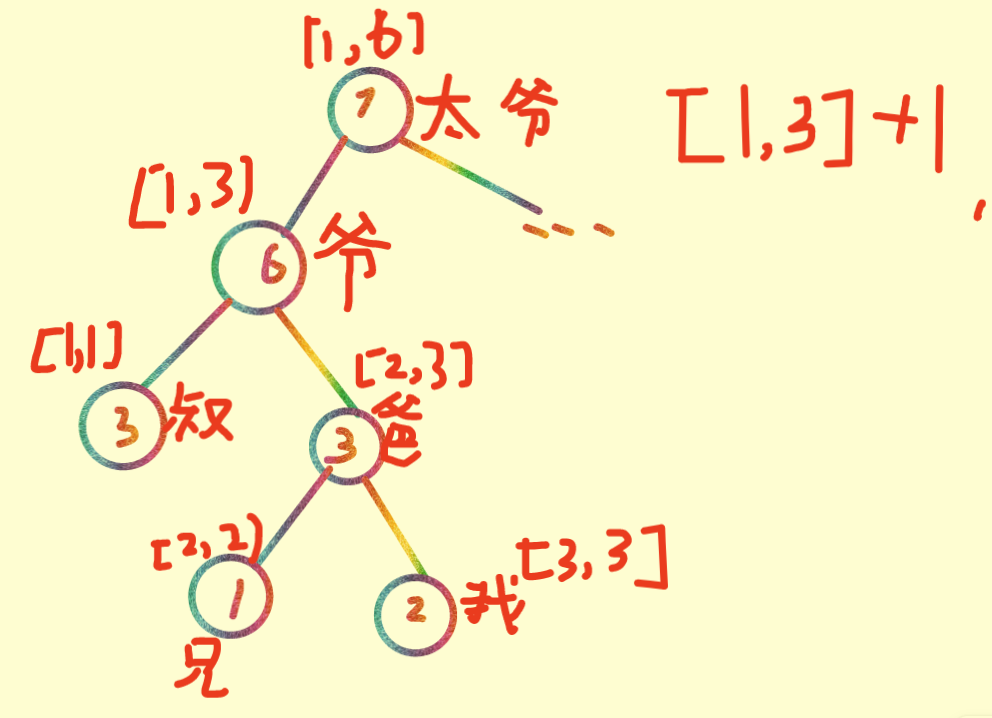
就比如发压岁钱,一次操作是太爷爷要发给[1,3]1块压岁钱,那么先发到爷爷手里,但是爷爷很懒

想着:反正这Q是我们家族的(要发Q的区间包含了爷爷管的区间),我就暂时收这了! ψ(｀∇´)ψ 暂时不想下放,于是将lazy标记+1(太爷爷发的Q数),并且因为爷爷节点储存的是以他根的树的子节点的Q总数,所以他自己的sumv自然要+1*4(太爷爷发的Q数*爷爷代表的区间长度r-l+1)；

然后不要忘记递归回去时还要将太爷爷的sumv更新。

那么此时这棵树就变成了这样:

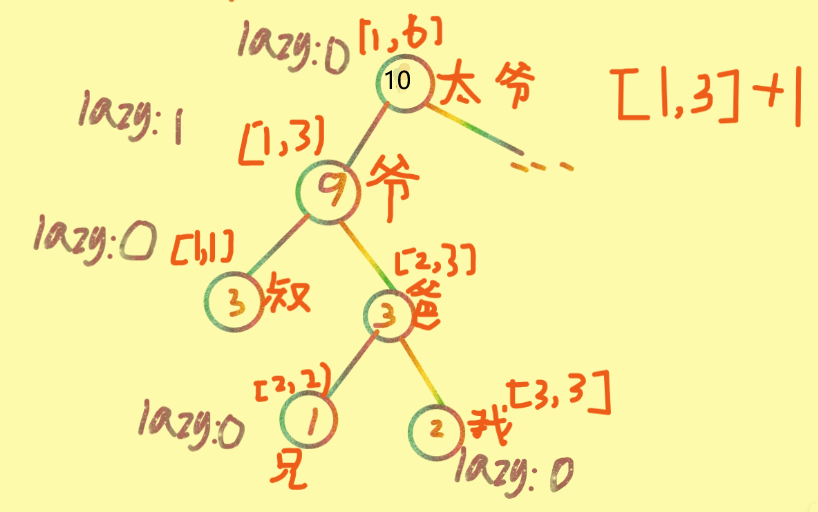
然后太爷爷一天突然心情大好,于是又发了一些钱,也就是给[2,3]2块压岁钱,那么先会发到爷爷手里。但是爷爷发现这笔Q要发放的区间不是由他管理,而是由他的儿孙中的一个管理,所以爷爷只能先将手中的压岁Q下放,在递归左右孩子(因为如果不先把压岁Q下放的话后面更新的值会错)。＞﹏＜

在这里插一句嘴QwQ:下放操作是这样的,首先将id的左孩子的lazy+它的lazy,再将id左孩子的Q+它下放的Q*左孩子区间长度(右孩子的这2步操作同理)(可以看做这个家族的所有人都很懒

),最后不要忘了还要把lazy[id]清空(详见代码)

下放后:

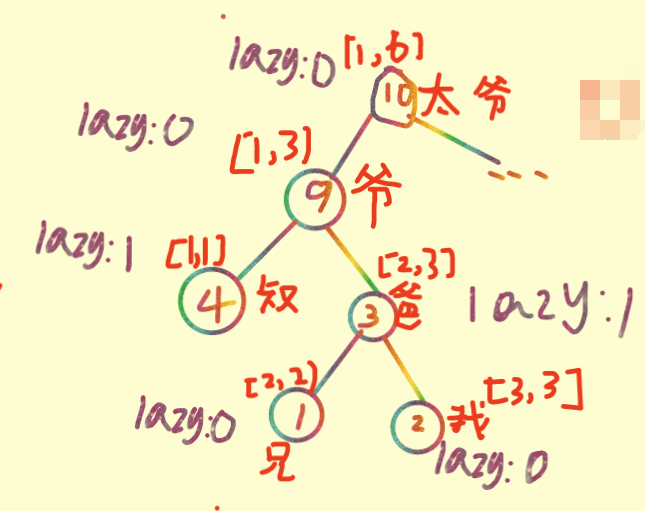
我们继续。当到了叔叔的区间时会发现:叔叔的左区间<太爷爷要发压岁Q的左区间,也就是说叔叔即他的儿孙并不会被太爷爷发压岁Q。所以继续递归到爸爸的区间,此时爸爸发现这Q是我们家族的(要发Q的区间包含了爸爸管的区间),而他传承了爷爷的"优良"传统,也很懒 o(*￣▽￣*)ブ暂时不想下放,于是将lazy标记+2(太爷爷发的Q数),并且因为爸爸节点储存的是以他根的树的子节点的Q总数,所以他自己的sumv自然要+1*2(太爷爷发的Q数*爸爸代表的区间长度r-l+1)；

然后不要忘记递归回去时还要将,爷爷,太爷爷的sumv更新。

那么此时这棵树变成了这样:

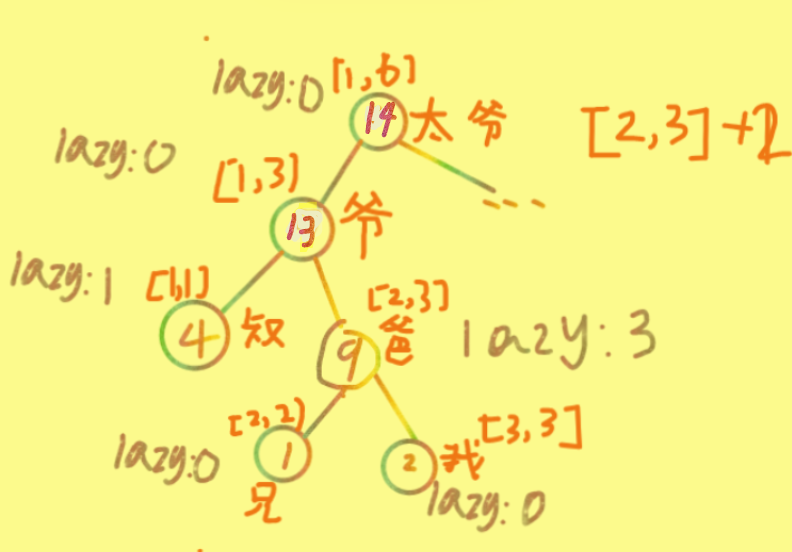
代码(更新)

void push_up(int id)
{sumv[id] = sumv[id * 2] + sumv[id * 2 + 1];
}
void push_down(int id,int l,int r)
{if(lazy[id])//如果id有lazy标记{int mid = (l + r) / 2;lazy[id * 2] += lazy[id];//将它的左孩子的lazy加上它的lazylazy[id * 2 + 1] += lazy[id];//将它的右孩子的lazy加上它的lazysumv[id * 2] += lazy[id] * (mid - l + 1);//左孩子的Q+它下放的Q*区间长度sumv[id * 2 + 1] += lazy[id] * (r - mid);lazy[id] = 0;//清空lazy标记}
}
void qjgx(int id,int l,int r,int x,int y,int v)//id:目前查到的节点编号  目前区间为[l,r]  目标是讲[x,y]的所有数+v
{if(l >= x && r <= y)//[l,r]被[x,y]包含了{lazy[id] += v;//暂时不下放Q,加进lazy标记中sumv[id] += v * (r - l + 1);//将Q收入囊中return ;}push_down(id,l,r);//要来更新下面节点了,赶紧下放Qint mid = (l + r) / 2;if(x <= mid) qjgx(id * 2,l,mid,x,y,v);//因为只有x<=mid(即[l,mid]有一部分是被[x,y]覆盖了的)才需要去更新[l,mid]if(y > mid) qjgx(id * 2 + 1,mid + 1,r,x,y,v);push_up(id);//子节点更新完之后父节点当然也要更新(上升操作)
}

思路(查询)

书接上回。一次太爷爷去别人家做客时发现大人们总是把过年的压岁Q"帮"孩子们收着,美名曰"保管"(其实就是强占),于是太爷爷决定去查询一下孩子们的压岁Q有没有发放到位￣へ￣

比如他要查询的是[1,2]那么首先要查询的是爷爷,然后发现爷爷的区间[1,3]并没有被包含在[1,2]中,所以先下放lazy(因为此时爷爷lazy为0,所以相当与没下放 ╮(╯-╰)╭ )然后爷爷就继续查询到叔叔,发现叔叔的去见被完全包含在了[1,3]中,所以返回叔叔的值4,然后从爷爷继续递归到了爸爸,发现爸爸的区间[2,3]并没有被包含在[1,2]中,所以还是下放lazy(不然查到子节点时自己私拿孩子压岁Q的事就露陷了！

(っ °Д °;)っ

于是爸爸赶紧下放lazy,于是这棵树就变成了这样:

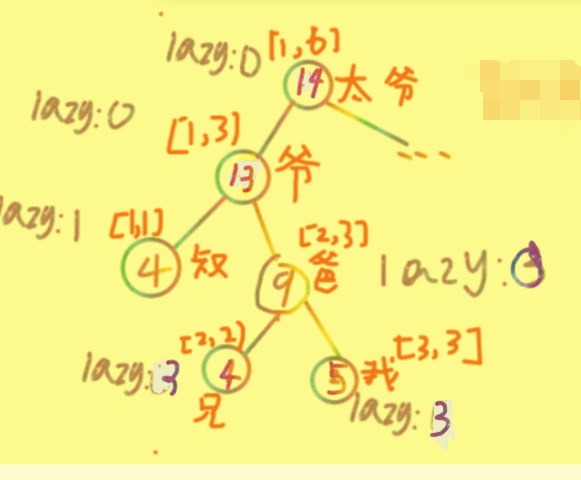
然后递归左孩子,发现被包含在了[1,2]中,返回4，右孩子没被包含,返回,然后爸爸返回4,爷爷返回4+4=8,所以最后太爷爷收到了8，大功告成!(●ˇ∀ˇ●)

代码(查询)

int find(int id,int l,int r,int x,int y)//id:目前查到的节点编号  目前区间为[l,r]  目标是求出[x,y]的和
{if(x <= l && r <= y) return sumv[id];//[l,r]被[x,y]包含了push_down(id,l,r);//要查到id的子节点了,赶紧下放int mid = (l + r) / 2,ans = 0;if(x <= mid) ans += find(id * 2,l,mid,x,y);//ans+=左孩子和if(y > mid) ans += find(id * 2 + 1,mid + 1,r,x,y);//ans+=右孩子和return ans;
}

三,例题

题目1(单点更新)

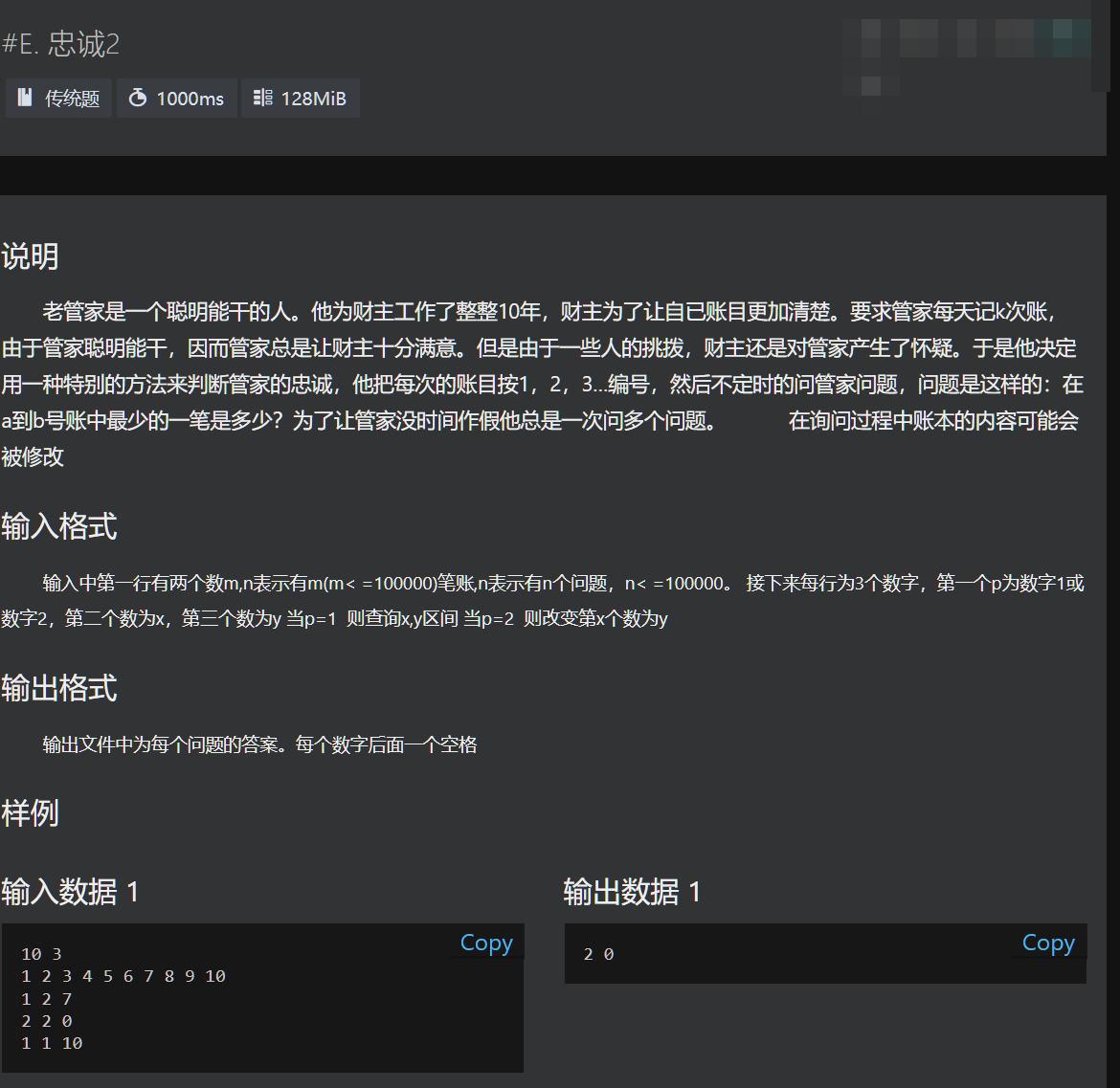
思路

先输入a数组,再创建线段树,最后每次输入时判断p是否为1,是则输出find(1,1,m,x,y);否则gexi(1,x,1,m,y)。

代码

#include <bits/stdc++.h>
using namespace std;
int tr[10000001];
int a[10000001];
void bui(int id,int l,int r)//创建线段树,id表示存储下标,区间[L,r]
{if(l == r){//叶子tr[id] = a[l];return ;}int mid = (l + r) / 2;bui(id * 2,l,mid);bui(id * 2 + 1,mid + 1,r);tr[id] = min(tr[id * 2],tr[id * 2 + 1]);
}
//id 表示树节点编号，l r 表示这个节点所对应的区间
//x y表示查询的区间
int find(int id,int l,int r,int x,int y)
{//需要查询的区间[x,y]将当前区间[l,r]包含的时候if(x <= l && r <= y) return tr[id];int mid = (l + r) / 2,ans = INT_MAX;if(x <= mid) ans = min(ans,find(id * 2,l,mid,x,y));if(y > mid) ans = min(ans,find(id * 2 + 1,mid + 1,r,x,y));return ans;
}
void gexi(int k,int id,int l,int r,int num)
{if(l == r){tr[k] = num;return ;}int mid = (l + r) / 2;if(id <= mid)gexi(k * 2,id,l,mid,num);elsegexi(k * 2 + 1,id,mid + 1,r,num);tr[k] = min(tr[k * 2],tr[k * 2 + 1]);
}
signed main()
{int n,m;cin>>m>>n;for(int i = 1; i <= m; i++) cin>>a[i];bui(1,1,m);while(n--){int x,y,p;cin>>p>>x>>y;if(p == 1) cout<<find(1,1,m,x,y)<<' ';else gexi(1,x,1,m,y);}return 0;
}

例题2(区间更新)

思路

套模板即可。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
int sumv[10000001],n,m,a[10000001],lazy[10000001];
void push_up(int id)
{sumv[id] = sumv[id * 2] + sumv[id * 2 + 1];
}
void push_down(int id,int l,int r)
{if(lazy[id])//如果id有lazy标记{int mid = (l + r) / 2;lazy[id * 2] += lazy[id];//将它的左孩子的lazy加上它的lazylazy[id * 2 + 1] += lazy[id];//将它的右孩子的lazy加上它的lazysumv[id * 2] += lazy[id] * (mid - l + 1);//左孩子的Q+它下放的Q*区间长度sumv[id * 2 + 1] += lazy[id] * (r - mid);lazy[id] = 0;//清空lazy标记}
}
void bui(int id,int l,int r)
{if(l == r)//叶子节点{sumv[id] = a[l];return ;}int mid = (l + r) / 2;bui(id * 2,l,mid);//递归创建左子树bui(id * 2 + 1,mid + 1,r);//递归创建右子树sumv[id] = sumv[id * 2] + sumv[id * 2 + 1];//左子树和+右子树和
}
void qjgx(int id,int l,int r,int x,int y,int v)//id:目前查到的节点编号  目前区间为[l,r]  目标是讲[x,y]的所有数+v
{if(l >= x && r <= y)//[l,r]被[x,y]包含了{lazy[id] += v;//暂时不下放Q,加进lazy标记中sumv[id] += v * (r - l + 1);//将Q收入囊中return ;}push_down(id,l,r);//要来更新下面节点了,赶紧下放Qint mid = (l + r) / 2;if(x <= mid) qjgx(id * 2,l,mid,x,y,v);//因为只有x<=mid(即[l,mid]有一部分是被[x,y]覆盖了的)才需要去更新[l,mid]if(y > mid) qjgx(id * 2 + 1,mid + 1,r,x,y,v);push_up(id);//子节点更新完之后父节点当然也要更新(上升操作)
}
int find(int id,int l,int r,int x,int y)//id:目前查到的节点编号  目前区间为[l,r]  目标是求出[x,y]的和
{if(x <= l && r <= y) return sumv[id];//[l,r]被[x,y]包含了push_down(id,l,r);//要查到id的子节点了,赶紧下放int mid = (l + r) / 2,ans = 0;if(x <= mid) ans += find(id * 2,l,mid,x,y);//ans+=左孩子和if(y > mid) ans += find(id * 2 + 1,mid + 1,r,x,y);//ans+=右孩子和return ans;
}
signed main()
{cin>>n>>m;for(int i = 1; i <= n; i++) cin>>a[i];bui(1,1,n);while(m--){int k,x,y,p;cin>>p>>x>>y;if(p == 1){cin>>k;qjgx(1,1,n,x,y,k);}else cout<<find(1,1,n,x,y)<<'\n';}return 0;
}