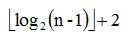什么是李超线段树
先以一个问题引入:
在平面上有两种操作(强制在线):
插入一条表达式为 L : y = k*x+b 的直线,给出 k ,b 。
给出 t,求当前所有直线中与直线 x = t 交点的纵坐标最大是多少
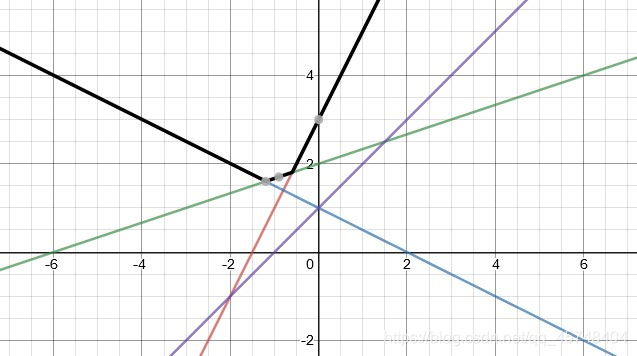
直线取 max 应该是得到一个下凸包,像这样(黑色的):
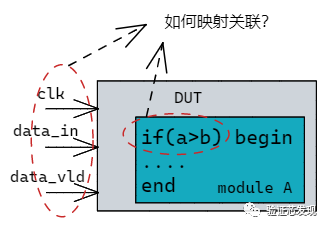
李超线段树是什么?线段树,当然是要维护区间 [L , R] 的一个信息,李超线段树维护的就是中点处最高的直线
比如下图,区间 [ 0 , 4 ] 的中点 x = 2 的最高直线为红色直线

利用这一信息,可以在 O(log n ) 的复杂度内插入直线、查询与 x = t 相交的最高点。(这里的 n 指的是查询的 t 的值域范围)
实现李超线段树
- 插入直线
李超线段树有一个非常重要的思想:标记永久化。
于是我们可以这样实现李超线段树,假如要把直线 L 插入某一区间:
- 如果当前区间还没有直线标记(不代表没有直线覆盖,因为标记永久化),那么就把标记记为L ;
- 如果 L 完全覆盖原有线段,像这样(蓝色是 L,红色是原有线段):

那么 x = t 与 [L,R] 的交点一定高于原线段,于是把原有线段直接替换为 L ; - 如果 L 被原有线段完全覆盖(就是2.反过来),那么 L 一定没有原有线段优;这样的话就舍弃 L 不做任何更新。
- 如果 L 和原有线段在 [ L , R ] 中有交点,像这样:
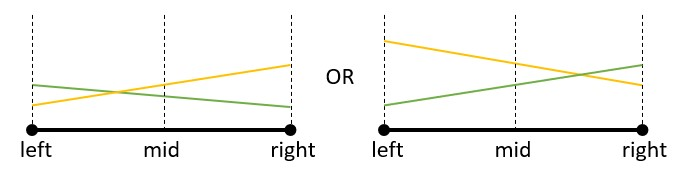
这种情况就无法确定 与哪条直线交点更高。根据李超线段树维护的信息,我们需要在两条直线中取与 x = mid 交点更高的一条直线作为标记(也就是上图的黄色直线,剩下的那条就是绿色直线)。再判断交点:如果在左区间,那么绿色直线在左区间可能比黄色直线高,然后就尝试把绿色直线往左区间插入;右区间类似。
-
查询
由于是标记永久化,查询就比较类似于标记永久化的线段树。比如查询 x = pos 的最高交点,那么就要从线段树一层层递归,直到递归到 [pos , pos] 这个区间——把每个区间的最优线段的交点取 max。 -
比如这样:
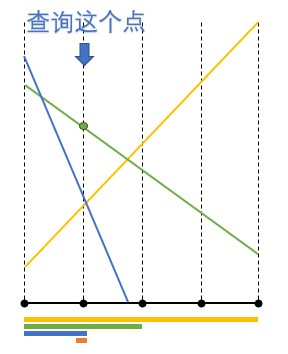
(下面的黄、绿、蓝、橙色线段表现了递归区间的过程)
P4254 [JSOI2008]Blue Mary开公司
#include<bits/stdc++.h>
#include <unordered_map>
using namespace std;
template<class...Args>
void debug(Args... args) {//Parameter packauto tmp = { (cout << args << ' ', 0)... };cout << "\n";
}
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>pll;
typedef pair<int, int>pii;
const ll N = 1e6 + 5;
const ll MOD = 998244353;
const ll INF = 0x7fffffff;
const double eps = 1e-12;
struct line {//线段double k, b;//斜率和与y轴int l, r;int flag;
}tree[N<<2];//线段树的定义
double calc(line a, int pos) { return a.k * pos + a.b; }//计算某条线段在某一个横坐标的纵坐标值
int cross(line a, line b) { return floor((a.b - b.b) / (b.k - a.k)); }//求两条线段交点的横坐标
void build(int root, int l, int r){tree[root]={0,0,1,50000,0};if (l == r)return;int mid = (l + r) >> 1;build(root << 1, l, mid); build(root << 1 | 1, mid + 1, r);
}
void modify(int root, int l, int r, line k){if (k.l <= l && r <= k.r) {//1.这个区间内没有记录有过优势线段:直接把这个区间的势线段修改为这条线段if (!tree[root].flag)tree[root] = k, tree[root].flag = 1;//2.新线段完全覆盖了之前记录的线段:优势线段为新线段,直接赋值替换else if (calc(k, l) - calc(tree[root], l) > eps && calc(k, r) - calc(tree[root], r) > eps)tree[root] = k;//3.区间内线段有交点的情况:判断哪根线段为优势线段,把区间记录的值给修改一下,然后把短的那一半递归处理else if (calc(k, l) - calc(tree[root], l) > eps || calc(k, r) - calc(tree[root], r) > eps) {int mid = (l + r) >> 1;//取出区间的中点if (calc(k, mid) - calc(tree[root], mid) > eps) {//与中点交点更高的一条直线作为优势线段line tmp = k; k = tree[root]; tree[root] = tmp;}//交点在中点的左侧,此时老线可能比被标记的优势线段高需要修改if (mid - cross(k, tree[root]) > eps)modify(root << 1, l, mid, k);//交点在中点的右侧,同理需要修改右侧区间的优势线段else modify(root << 1 | 1, mid + 1, r, k);}}else {//要修改线段的区间没完全包含在某根节点的区间范围内int mid = (l + r) >> 1;if (k.l <= mid)modify(root << 1, l, mid, k);if (mid < k.r)modify(root << 1 | 1, mid + 1, r, k);}
}
double query(int root, int l, int r, int x){//由于是标记永久化,查询就比较类似于标记永久化的线段树//那么就要从线段树一层层递归,直到递归到某个点//每个区间的最优线段的交点取 maxif (l == r)return calc(tree[root], x);else {int mid = (l + r) >> 1;double ans = calc(tree[root], x);if (x <= mid)return max(ans, query(root << 1, l, mid, x));else return max(ans, query(root << 1 | 1, mid + 1, r, x));}
}
int main() {ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);int n;cin >> n;build(1, 1, 50000);for (int i = 1; i <= n; i++) {string op;cin >> op;if (op[0] == 'P') {double s, p;cin >> s >> p;line now; now.l = 1; now.r = 50000; now.k = p; now.b = s - p;modify(1, 1, 50000, now);}else {int x;cin >> x;cout << floor(query(1, 1, 50000, x) / 100) << "\n";}}return 0;
}