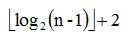线段树描述：
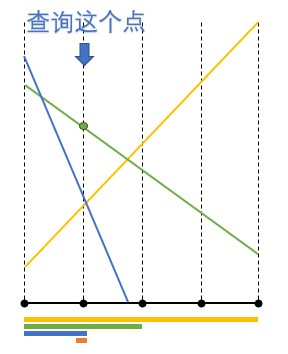
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。
例图如下：

代码实现如下：主要实现了线段树的构建，单点更新、区间和、最大值和一些测试用例

import java.util.Scanner;
public class Xds {//线段树的实现    我们都是默认从下标为1开始的  编号寻找为左节点2*i  右节点为2*i+//线段树节点（用于建立线段树节点对象数组）static class Tree{int left;//记录当前节点左边界int right;//记录当前节点又边界int max;//记录当前节点的最大值int sum;//记录当前节点的所有和public Tree() {}@Overridepublic String toString() {return "Tree{" +"left=" + left +", right=" + right +", max=" + max +", sum=" + sum +'}';}}//构建线段树public static void build(int u,int left,int right,int[] a,Tree[] trees){//建立线段树函数   u表示当前节点的编号 a表示要建立线段树的原数组trees[u].left=left;//当前节点的左边界trees[u].right=right;//当前节点的又边界if(left==right){//表示到达了叶子节点trees[u].max=a[left];trees[u].sum=a[left];return;}else {int mid = (left + right) >>1;//计算中点的坐标build(2 * u, left, mid, a, trees);//递归解决所有节点信息build(2 * u + 1, mid + 1, right, a, trees);trees[u].max = Math.max(trees[2 * u].max, trees[2 * u + 1].max);//记录当前节点的最大值trees[u].sum=trees[2*u].sum+trees[2*u+1].sum;//记录当前节点的left和right之间的sum和}}//查找线段树指定范围之间的最大值public static int getMax(int left,int right,Tree[] trees,int u){//u表示当前节点的位置int mid=(trees[u].left+trees[u].right)>>1;//递归出口  到达叶子节点或者左右节点包含的情况下if (trees[u].left==trees[u].right||(left<=trees[u].left&&right>=trees[u].right)) return trees[u].max;if(right<=mid){//如果右边界小于中点的标号，则走左边界return getMax(left,right,trees,2*u);}else if (left>mid){//如果左边界大于中点的标号，则走右边界return getMax(left,right,trees,2*u+1);}else {int temp=getMax(left,mid,trees,2*u);//找到左边的最值int temp1=getMax(mid+1,right,trees,2*u+1);//找到右边的最值return Math.max(temp,temp1);}}//查找线段树指定范围之间的所有和public static int getSum(int left,int right,Tree[] trees,int u){int mid=(trees[u].left+trees[u].right)>>1;//递归出口  到达叶子节点或者左右节点对应相等的情况下if (trees[u].left==trees[u].right||(left==trees[u].left&&right==trees[u].right)) return trees[u].sum;if(right<=mid){//如果右边界小于中点的标号，则走左边界return getSum(left,right,trees,2*u);}else if (left>mid){//如果左边界大于中点的标号，则走右边界return getSum(left,right,trees,2*u+1);}else {int temp=getSum(left,mid,trees,2*u);//找到左边的所有和int temp1=getSum(mid+1,right,trees,2*u+1);//找到右边的所有和return temp+temp1;}}//寻找下标为index的元素在trees中的下标public static int getIndex(int index,Tree[] trees,int u){ //u表示trees的当前节点的下标 初始值为1//递归出口if (trees[u].left==index&&trees[u].right==index){//左右边界值相等return u;//返回在trees数组中的下标}int left=trees[u].left;//找到当前节点左边界int right=trees[u].right;//找到当前节点的有边界int mid=(left+right)>>1;if (index<=mid){//找到左边边界return getIndex(index,trees,2*u);}else return getIndex(index,trees,2*u+1);}//修改线段树内容(点更新)public static void update(int index,int value,Tree[] trees,int u){//将下标为index的值转换为value  u表示trees的当前节点的下标 初始值为1int i=getIndex(index,trees,u);//找到index的对应trees数组中的下标trees[i].max=value;//更新其叶子节点的max和value值trees[i].sum=value;i=i>>1;while (i>=u){//若i变为根节点的编号u，则退出循环 向上回溯解决修改节点值trees[i].max=Math.max(trees[2*i].max,trees[2*i+1].max);trees[i].sum=trees[2*i].sum+trees[2*i+1].sum;i=i>>1;}}//测试public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n=scanner.nextInt();//输入数组的大小int[] a=new int[n+1];for (int i = 1; i <=n ; i++) {a[i]=scanner.nextInt();}Tree[] trees=new Tree[4*n];//空间开4倍的数组长度大小for (int i = 0; i <4*n ; i++) {//防止空指针 所以需要每个都进行初始化trees[i]=new Tree();}build(1,1,n,a,trees);for (int i = 1; i <4*n ; i++) {System.out.println(trees[i].toString());}System.out.println("index "+getIndex(2,trees,1));System.out.println("max "+getMax(1,3,trees,1));System.out.println("sum "+getSum(1,4,trees,1));update(2,5,trees,1);//将元素组a的下标为2的值改为5for (int i = 1; i <4*n ; i++) {System.out.println(trees[i].toString());}System.out.println("index "+getIndex(2,trees,1));System.out.println("max "+getMax(1,3,trees,1));System.out.println("sum "+getSum(1,4,trees,1));}
}

运行结果如下：