判断一个点是否在圆内（三点确定一个圆）

article/2025/11/6 22:35:34

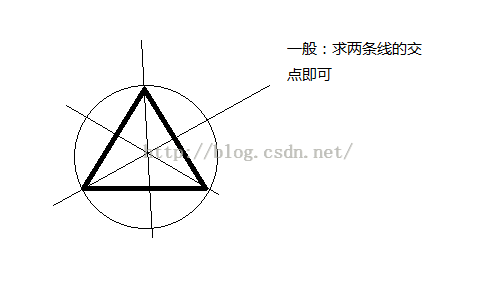
三角形的外接圆圆心是任意两边的垂直平分线的交点。 三角形外接圆圆心叫外心。

        /// <summary>/// Returns true if the point (p) lies inside the circumcircle made up by points (p1,p2,p3)/// </summary>/// <remarks>/// NOTE: A point on the edge is inside the circumcircle/// </remarks>/// <param name="p">Point to check</param>/// <param name="p1">First point on circle</param>/// <param name="p2">Second point on circle</param>/// <param name="p3">Third point on circle</param>/// <returns>true if p is inside circle</returns>private static bool InCircle(Geometry.Point p, Geometry.Point p1, Geometry.Point p2, Geometry.Point p3){//Return TRUE if the point (xp,yp) lies inside the circumcircle//made up by points (x1,y1) (x2,y2) (x3,y3)//NOTE: A point on the edge is inside the circumcircle// 确定三个点是否组成三角形，三点共线则不构成圆if (System.Math.Abs(p1.Y - p2.Y) < double.Epsilon && System.Math.Abs(p2.Y - p3.Y) < double.Epsilon){//INCIRCUM - F - Points are coincident !!return false;}double m1, m2;double mx1, mx2;double my1, my2;double xc, yc;if (System.Math.Abs(p2.Y - p1.Y) < double.Epsilon){//计算边P2P3的垂直平分线的斜率m2 = -(p3.X - p2.X) / (p3.Y - p2.Y);//计算边P2P3的中点mx2 = (p2.X + p3.X) * 0.5;my2 = (p2.Y + p3.Y) * 0.5;//Calculate CircumCircle center (xc,yc)xc = (p2.X + p1.X) * 0.5;// 边P2P3与P1P2边的垂直平分线联立计算交点// y=xc 与 y=m2(x-mx2)+my2 联立得yc = m2 * (xc - mx2) + my2;}else if (System.Math.Abs(p3.Y - p2.Y) < double.Epsilon){//计算边P1P2的垂直平分线的斜率m1 = -(p2.X - p1.X) / (p2.Y - p1.Y);//计算边P1P2的中点mx1 = (p1.X + p2.X) * 0.5;my1 = (p1.Y + p2.Y) * 0.5;//Calculate CircumCircle center (xc,yc)// 边P2P3与P1P2边的垂直平分线联立计算交点// y=xc 与 y=m1(x-mx1)+my1 联立得xc = (p3.X + p2.X) * 0.5;yc = m1 * (xc - mx1) + my1;}else{   //计算边P1P2和P2P3的垂直平分线的斜率m1 = -(p2.X - p1.X) / (p2.Y - p1.Y);m2 = -(p3.X - p2.X) / (p3.Y - p2.Y);//计算边P1P2和P2P3的中点mx1 = (p1.X + p2.X) * 0.5;mx2 = (p2.X + p3.X) * 0.5;my1 = (p1.Y + p2.Y) * 0.5;my2 = (p2.Y + p3.Y) * 0.5;//Calculate CircumCircle center (xc,yc)// y=m1*(x-mx1)+my1 与 y=m2*(x-mx2)+my2 联立xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2);yc = m1 * (xc - mx1) + my1;}//计算圆的半径double dx = p2.X - xc;double dy = p2.Y - yc;double rsqr = dx * dx + dy * dy;//double r = Math.Sqrt(rsqr); //Circumcircle radius//计算点到圆心的距离dx = p.X - xc;dy = p.Y - yc;double drsqr = dx * dx + dy * dy;//判断点到圆心的距离是否小于圆的半径return (drsqr <= rsqr);}