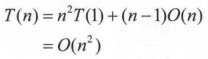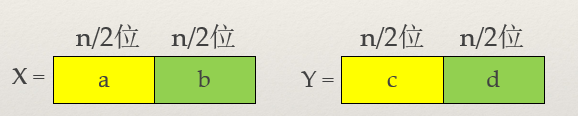数据的形式是多种多样的，维度也是各不相同的，当实际问题中遇到很高的维度时，如何给他降到较低的维度上？前文提到进行属性选择，当然这是一种很好的方法，这里另外提供一种从高维特征空间向低纬特征空间映射的思路。

数据降维的目的

　　数据降维，直观地好处是维度降低了，便于计算和可视化，其更深层次的意义在于有效信息的提取综合及无用信息的摈弃。

数据降维的方法

　　主要的方法是线性映射和非线性映射方法两大类。

线性映射

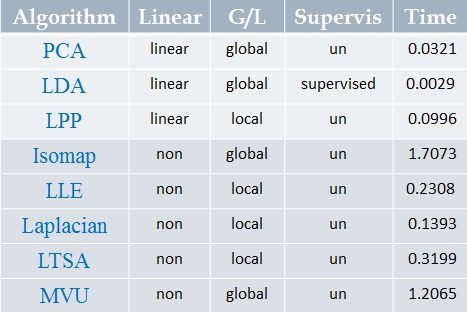
　　线性映射方法的代表方法有：PCA（Principal Component Analysis），LDA（Discriminant Analysis）

PCA方法简介

　　主成分分析的思想，就是线性代数里面的K-L变换，就是在均方误差准则下失真最小的一种变换。是将原空间变换到特征向量空间内，数学表示为$Ax=\lambda x$。
　　特征向量和特征值的意义：分别表示不同频率及其幅度。
　　特征向量和特征值的直白理解：想在特征空间内找到某个向量$x$，使得其满足$Ax=\lambda x$。这个式子可以这样理解，$A$是空间内的运动，$x$经过运动$A$后，保持方向不变（仍是$x$的方向），只是大小伸缩了$\lambda$倍。这样我们找到了$k$个这样的向量$\beta_k$。
　　$A*[\beta_1, \beta_2, ... ,\beta_k]=[\lambda_1\beta_1, \lambda_2\beta_2, ... , \lambda_k\beta_k]$。
　　当然在实际用时，取最大的前几个足矣。
　　PCA计算是用的协方差矩阵$U$的分解特征向量。
1. 样本矩阵去中心化（每个数据减去对应列的均值），得到$A_{m,n}$。$A_{m,n}$表示$m$个$n$维的数据。
　　2. $U$表示样本矩阵$A$的协方差矩阵($A^T*A$=$U$，因为去中心化后的$A^T*A$即协方差）
　　$E(X-X_0)(Y-Y_0)=\sum_{i=1}^m \frac{1}{m} (x_i-x_0)(y_i-y_0)$。
　　期望的定义：$E(x)=\sum x_i * p(x_i)$
　　3. $U=[\beta]*\Lambda*[\beta]^{-1}$
　　4. 对$A$在$[\beta_1, \beta_2, \beta_k]$方向上变换（注意选择$\lambda$大的特向映射）。
　　$U= \begin{bmatrix} cov(1,1) & cov(1,2) &...& cov(1,n) \\ cov(2,1) & cov(2,2) &...& cov(2,n) \\ 　　　　 ... ... ... ... \\cov(n,1) & cov(n,2) &...& cov(n,n)\end{bmatrix}$
　　其中数字表示相应第几个属性。
　　为什么要用协方差矩阵来特向分解呢？
　　协方差矩阵表征了变量之间的相关程度（维度之间关系）。
　　对数据相关性矩阵的特向分解，意味着找到最能表征属性相关性的特向（最能表征即误差平方最小）。PCA一开始就没打算对数据进行特向分解，而是对数据属性的相关性进行分析，从而表示出最能代表属性相关性的特向，然后将原始数据向这些特向上投影。所以，有的地方说PCA去相关。
　　PCA的原理推导：由最小误差平方准则引入，比（无）较（法）蛋（理）疼（解），暂时不做推导了（参考《模式分类》3.8节）。
　　PCA优缺点：
　　优点：1）最小误差。2）提取了主要信息
　　缺点：1）计算协方差矩阵，计算量大
　　上述PCA中的特向分解，必须为方阵，这个条件是很苛刻的。有没有直接对任意矩阵的分解呢，答案是有的，他的名字叫SVD分解。
　　SVD分解用来找到矩阵的主要部分。可以直接对数据矩阵进行分解。
　　$B_{m*n} \approx U_{m*k}\sum_{k*k}*V_{n*k}^T$
　　其中$U_{m*k}和V_{n*k}$是正交矩阵。
　　$B_{m*n} * V_{n*k} \approx U_{m*k}\sum_{k*k}*V_{n*k}^T* V_{n*k}$
　　$B_{m*n} * V_{n*k} \approx U_{m*k}\sum_{k*k} \approx \hat {A}_{m*k}$实现了降维。
　　$U_{m*k}^T*B_{m*n} \approx U_{m*k}^T*U_{m*k}\sum_{k*k}*V_{n*k}^T \approx \sum_{k*k}*V_{n*k}^T \approx \hat{A}_{k*n}$实现了压缩数据。
　　SVD怎么跟这个PCA结合到一起的呢？
　　SVD是对$A^TA$或者$AA^T$求解特值和特向，然后对$A$进行分解，得到$A=U \Delta V^T$，中间是奇异值对角阵。
　　$U$的列向量是$AA^T$的特向组成。
　　因此，可以用SVD求解特向，然后取前几个大的特值对应的特向进行降维。
　　PCA想对协方差矩阵特征向量求解，而$AA^T$刚好是协方差的表示形式，而$AA^T$的特向求解刚好是SVD分解的过程，且分解的酉矩阵的列向量刚好对应着$AA^T$的特向，于是PCA的协方差求解特向就变成了样本矩阵的SVD分解。
　　两个引理：
　　引理1：对于任何一个矩阵$A_{m*n}$都有：
　　$rank(AA^T)=rank(A^TA)=rank(A)$
　　引理2：对于任何一个矩阵$A$，都有$A^TA$与$AA^T$是半正定的Hermite矩阵。
　　定理1：$A^TA$的特征值也是$AA^T$的特值，反之亦然。
　　定理2：若$A$是正规矩阵 ，则$A$的奇异值是$A$的非零特征值的模长。
定理3：若$\delta_1 \geqslant \delta_2 \geqslant ... \geqslant \delta_r$是$A_{m*n}$的$r$个正奇异值，则存在$m$阶酉矩阵$U$和$n$阶酉矩阵$V$，满足：
$A=UDV^T=U \begin{bmatrix} \Delta & 0 \\ 0 & 0 \end{bmatrix} V^T$
　　其中， $\Delta = diag(\delta_1, \delta_2, ... , \delta_r)$
　　定理3证明过程表明$U$是$AA^T$的特征向量。此处略去证明，请自行查阅线性代数。
　　定理4：若$\delta_1 \geqslant \delta_2 \geqslant ... \geqslant \delta_r$是$A$的$r$个正奇异值，则总有次酉矩阵$U_{m*r}$,$V_{n*r}$满足：
　　$A=U_{m*r}\Delta V_{n*r}^T$
　　其中 $\Delta = diag(\delta_1, \delta_2, ... , \delta_r)$
　　特征值和奇异值怎么对应起来？
　　$A^TA \beta_i = \lambda_i \beta_i$
　　$\sigma_i = \sqrt {\lambda_i}$
　　$\mu_i = \frac{1}{\sigma_i}A\beta_i$
　　这个地方跟上面稍微有所不同，这里条件更宽松了。

LDA方法简介

　　LDA核心思想：往线性判别超平面的法向量上投影，使得区分度最大（高内聚，低耦合）。
　　具体内容见之前博客-“线性判别函数”的Fisher线性判别准则：http://blog.csdn.net/yujianmin1990/article/details/48007589
　　LDA优缺点：
　　优点：1）简单易于理解
　　缺点：2）计算较为复杂
　　PCA in Spark：http://blog.selfup.cn/1243.html

非线性映射

　　非线性映射方法的代表方法有：核方法（核+线性），二维化和张量化（二维+线性），流形学习（ISOMap，LLE，LPP）

基于核的非线性降维

　　代表方法有：KPCA，KFDA。
　　KPCA的基本思想：通过Kernel trick将PCA投影的过程通过内积的形式表达出来。将高维向量$\phi(x)与对应特向\beta$的内积转换成低维的核函数表示。

KPCA

　　
　　基于核的非线性降维方法的优缺点：
　　优点：具有核方法的优点。
　　缺点：核的不同选择影响效果。
　　（自己对KPCA这地方并不是完全搞懂了，需要再仔细看看）

二维化和张量化

　　将数据映射到二维空间上，常见算法比如二维主分量分析、二维线性判别分析、二维典型相关分析。
　　二维化和张量化优缺点：
　　优点：
　　1）计算效率高。
　　2）有些数据二维降维效果要明显好于一维降维。
　　缺点：
　　1）原理机制研究不透彻。

流形学习

　　流形学习的主要算法有：ISOMap（等距映射）、LE（拉普拉斯特征映射）、LLE（局部线性嵌入）。
　　流形：直线或者曲线是一维流形，平面或者曲面是二维流形，更高维之后是多维流形。一个流形好比是$d$维的空间，是一个$m$维空间（$m>n$）被扭曲之后的空间。流形并不是一个“形状”，而是一个“空间”
　　流形学习的假设：数据采样于某一流形上。

ISOMap

　　ISOMap是一种非迭代的全局优化算法。ISOMap对MDS（Multidimensional Scaling-多维尺度分析）进行改造，用测地线距离（曲线距离）作为空间中两点距离，原来是用欧氏距离，从而将位于某维流形上的数据映射到一个欧氏空间上。
　　ISOMap将数据点连接起来构成一个邻接Graph来离散地近似原来流形，而测地距离则相应地通过Graph上的最短路径来近似了。
　　比如：我们将球体曲面映射到二维平面上。
　　此博客写得通俗易懂：http://blog.pluskid.org/?p=533
　　几点注意：
　　1）ISOMap适用的流形：适合于内部平坦的低维流形，不适合于学习有较大内在曲率的流形。
　　2）近邻数的选择：近邻数应足够大以便能够减少在路径长度和真实测地距离之间的不同，但要小到能够预防“短路”现象。
　　3）所构造图的连通性：要求所构造的图示连通的，否则有两种处理办法，一种是放宽临界点选择的限制，另一种是对于每一连通部分分别使用ISOMap算法，得到不同部分的降维结果。
　　数据到底是否分布于一个流形上？这是个暂时难以回答的问题。
　　MDS是一种降维方法，它在降维时使得降维之后的两点间的欧氏距离尽量保持不变（用欧氏距离矩阵来表示高维向量的两两之间的相似度，寻找同样数量的映射维度的向量，使得映射维度下两两间距离约等于原高维下两两间距离，变为了优化问题）。维基百科对MDS的介绍https://en.wikipedia.org/wiki/Multidimensional_scaling

LLE

　　前提假设：数据没有形成一个封闭的超曲面，局部数据点是线性的。
　　LLE（Locally Linear Embedding-局部线性嵌入）用局部线性反映全局的非线性的算法，并能够使降维的数据保持原有数据的拓扑结构。（在流形上使用局部线性，并用有限局部样本的互相线性表示，得到几何特性的构造权重矩阵，在低维下找到满足高维时样本间构造权重的样本集）
　　
　　LLE步骤如下：
　　1.计算或者寻找数据点$x_i$的临近数据点。
　　　　假设数据局部为平面，故可以用线性组合表示$x_i$，其误差为：
　　　　$e(w)=\sum_{i=1}^m||x_i-\sum_{j=1}^Kw_{ij}x_j||^2$； $\sum_{j=1}^Kw_{ij}=1$
　　　　其中$w_{ij}$表示线性重构$x_i$时的贡献比例。
　　　　找到每个样本点的$K$个最近邻点。
2.计算构造权重并重构数据
通过约束计算$w_{ij}$，使得不在该样本点的$K$个最近邻点中的构造权重都为0.
重构权重使得重构的数据点与临近点间的旋转、缩放、平移特性保持不变，即几何特性不依赖于特定的参考框架。
3.由重构样本向低维映射。（求低维嵌入）
设$z$是低维空间，找到同样数量的低维映射样本，使得：
　　　　$e=\sum_{i=1}^m||\phi(x_i)-\sum_{j=1}^Kw_{ij}\phi(x_{ij})||^2$
　　　　$e=\sum_{i=1}^m||z_i-\sum_{j=1}^Kw_{ij}z_{ij}||^2$
　　　　最小。（不去关心$\phi$，直接找$z_i$）
　　流形学习优缺点：
　　优点：1）假设流形的存在，部分解决了高维数据分布的问题。
　　缺点：1）假设流形的存在，不能总是适合数据特点。

其他方法

　　其他方法：深度学习，聚类降维
　　深度学习降维优缺点：
　　优点：1）所提取特征的代表性强
　　缺点：1）可解释性差。2）目的性不强
　　聚类降维优缺点：
　　暂时未看这部分内容

小结

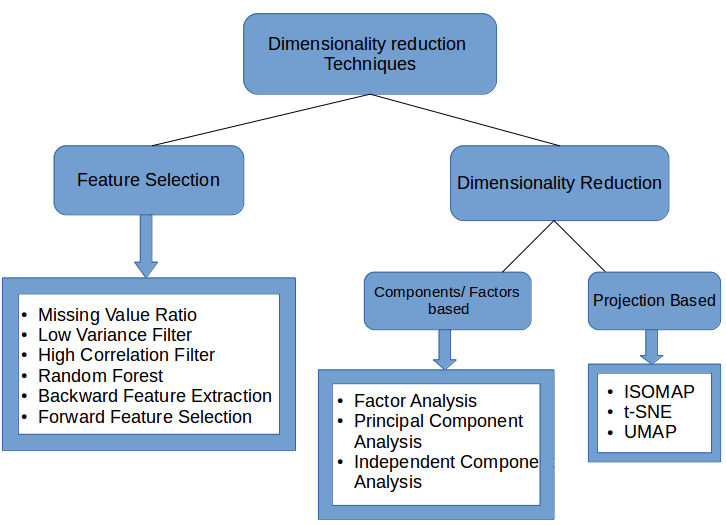
　　降维方法 __ 属性选择：过滤法；包装法；嵌入法；
　　　　　　|_ 映射方法 _线性映射方法：PCA、FDA等
　　　　　　　　　　　　|_非线性映射方法：
　　　　　　　　　　　　　　　　　　　　　　|__核方法：KPCA、KFDA等
　　　　　　　　　　　　　　　　　　　　　　|__二维化：
　　　　　　　　　　　　　　　　　　　　　　|__流形学习：ISOMap、LLE、LPP等。
　　　　　　　　　　　　|__其他方法：神经网络和聚类
　　　　　　　　　　　　
　　降维可以方便数据可视化+数据分析+数据压缩+数据提取等。
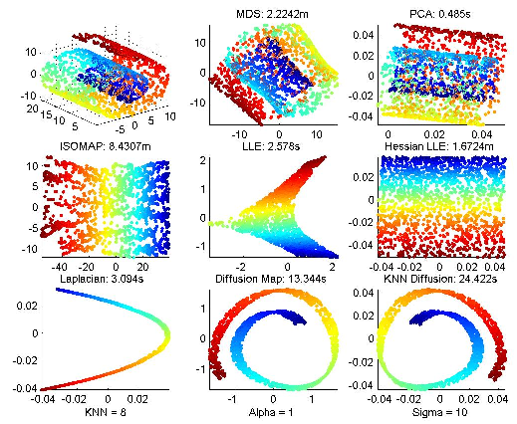
　　各个降维方法效果图展示：