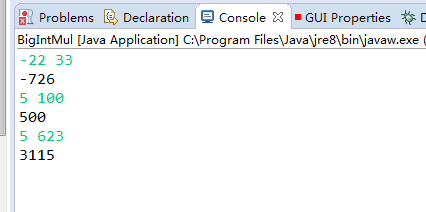
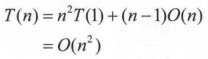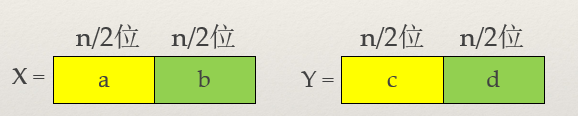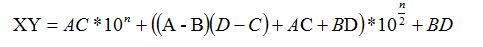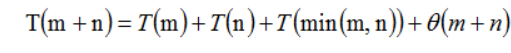大整数的乘法
(这里主要讨论的是两个较大的数相乘的效率问题,实际上并不是真正意义上的大数相乘。在java中有个BigInteger类已经可以储存大数,并提供了大数相乘的方法了。)
【分析】
首先,当两个整数X、Y(位数分别为n、m)进行相乘时,我们可以将这两个整数分别进行分割。
假设 n == m 并且 n 是2的幂,将n位的整数X和Y都分为2段,分别记为A、B和C、D。这时每段长为 n / 2位。
此时,X = A10^(n/2) + B,Y = C10^(n/2) + D。
那么XY = AC10^n + ((A - B)(D - C) + AC + BD)10^(n/2) + BD。
经过算法效率的分析,我们可以知道,T(n) = O(n^log3)。
这里我们要考虑几个问题:
问题1:当n 不等于 m时,我们如何使得两个整数的位数保持相等又不影响结果呢?
我们可以将这两个整数以字符串的形式进行存储,当这两个整数的位数不相等时,我们可以在这两个整数调用算法进行相乘之前,再次初始化这两个字符串,在字符串的前面补加0,此时并不会影响到最终的结果。
问题2:当我们用字符串存储这两个整数的时候,又应该如何考虑整数的符号问题呢?当出现负整数的时候,我们将要考虑到如何截取整数的问题。
我们可以创建一个BigNum类,用一个字符串类型存储这个整数的值,用一个int类型存储这个整数的符号。在创建对象的时候,如果字符串存储的是负整数,那么就应该将这个字符串截取出除符号外的部分来初始化这个对象的字符串属性,并且符号根据具体整数赋值1或0,1表示正整数,0表示负整数。
问题3:假如n不是2的幂,那我们应该怎么做呢?
我们可以在初始化这两个字符串的同时,往字符串的前面补0,直到这两个字符串的长度为奇数为止。
此外,根据上述所提出来的公式
XY = AC10^n + ((A - B)(D - C) + AC + BD)10^(n/2) + BD
采用分治法设计算法,定义一个multi(BigNum x, BigNum y)方法,那么有以下伪代码:
BigNum multi(BigNum x, BigNum y) {
初始化x和y的字符串属性(适当补0操作);
分x的字符串为两段A和B、分y的字符串为两段C和D;
根据A、B、C、D创建相应的BigNum对象a, b, c, d;
multi(a, c)计算AC的值;
对AC进行后面补0的操作,相当于乘以10^n;
multi(b, d)计算BD的值;
return 计算AC10^n + ((A - B)(D - C) + AC + BD)10^(n/2) + BD的值;
}
【程序】
用java语言编写程序,代码如下:
import java.util.Scanner;public class BigIntMul {public static void main(String[] args) {Scanner input = new Scanner(System.in);while(input.hasNext()) {String s1 = input.next();String s2 = input.next();BigNum b1 = new BigNum(s1);BigNum b2 = new BigNum(s2);BigNum r = multi(b1, b2);String s = r.n == 0 ? "-" : "";System.out.println(s + r.s);}}//定义大整数类static class BigNum {String s;int n;//存储大整数的正负号,1表示正,0表示负//定义BigNum对象,根据字符串的值,定义符号public BigNum(String s) {if(s.charAt(0) == '-') {n = 0;this.s = s.substring(1, s.length());}else {n = 1;this.s = s;}if(Long.parseLong(s) == 0)n = 1;} //定义BigNum对象,符号自定义public BigNum(String s, int n) {if(s.charAt(0) == '-')this.s = s.substring(1, s.length());elsethis.s = s;this.n = n;if(Long.parseLong(s) == 0)n = 1;}public BigNum() {}public int len() {return s.length();}}//初始化两个BigNum对象,使得两个对象的值位数相等,且位数为偶数。不足的话前面为补0,并返回长度。//当两个数的长度相等,并且长度为1时,则直接返回长度值1public static int init(BigNum b1, BigNum b2) {int n;int len1 = b1.s.length();int len2 = b2.s.length();if(len1 > len2) {if(len1 % 2 != 0) {b1.s = "0" + b1.s;len1++;}n = len1;for(int i = 0; i < len1 - len2; i++)b2.s = "0" + b2.s;}else if(len1 < len2) {if(len2 % 2 != 0) {b2.s = "0" + b2.s;len2++;}n = len2;for(int i = 0; i < len2 - len1; i++)b1.s = "0" + b1.s;}else {if(len1 == 1)return 1;if(len1 % 2 != 0) {b1.s = "0" + b1.s;b2.s = "0" + b2.s;len1++;}n = len1;}return n;}public static BigNum multi(BigNum b1, BigNum b2) {int n = init(b1, b2);//当两个数的长度为1时,直接让这两个数相乘,返回BigNum对象。if(n == 1) {BigNum r = new BigNum();if((b1.n == 0 && b2.n == 1) || (b1.n == 1 && b2.n == 0))r.n = 0;elser.n = 1;long n1 = Long.parseLong(b1.s);long n2 = Long.parseLong(b2.s);r.s = (n1 * n2) + "";if(n1 == 0 || n2 == 0)r.n = 1;return r;}//将整数分为两个数,且不论这个整数是否为正数或负数,都将分解出来的数的符号定义为正号。//根据公式计算结果。BigNum a = new BigNum(b1.s.substring(0, n / 2), 1);BigNum b = new BigNum(b1.s.substring(n / 2, n), 1);BigNum c = new BigNum(b2.s.substring(0, n / 2), 1);BigNum d = new BigNum(b2.s.substring(n / 2, n), 1);BigNum ac = multi(a, c);BigNum bd = multi(b, d);long aa1 = /*a.n == 0 ? (-1) * Long.parseLong(a.s) : */Long.parseLong(a.s);long bb1 = /*b.n == 0 ? (-1) * Long.parseLong(b.s) : */Long.parseLong(b.s);long a_bl = aa1 - bb1;BigNum a_b = new BigNum(a_bl + "");long dd1 = /*d.n == 0 ? (-1) * Long.parseLong(d.s) : */Long.parseLong(d.s);long cc1 = /*c.n == 0 ? (-1) * Long.parseLong(c.s) : */Long.parseLong(c.s);long d_cl = dd1 - cc1;BigNum d_c = new BigNum(d_cl + "");BigNum abcd = multi(a_b, d_c);BigNum r1 = new BigNum(ac.s);for(int i = 0; i < n; i++) {r1.s = r1.s + "0";}long labcd = abcd.n == 0 ? (-1) * Long.parseLong(abcd.s) : Long.parseLong(abcd.s);long lac = ac.n == 0 ? (-1) * Long.parseLong(ac.s) : Long.parseLong(ac.s);long lbd = bd.n == 0 ? (-1) * Long.parseLong(bd.s) : Long.parseLong(bd.s);long lr2 = labcd + lac + lbd;BigNum r2 = new BigNum(lr2 + "");for(int i = 0; i < n / 2; i++)r2.s = r2.s + "0";long lr3 = lac * (long)(Math.pow(10, n)) + lr2 * (long)(Math.pow(10, n / 2)) + lbd;BigNum r3 = new BigNum(lr3 + "");if((b1.n == 0 && b2.n == 1) || (b1.n == 1 && b2.n == 0))r3.n = 0;elser3.n = 1;if(lr3 == 0)r3.n = 1;return r3;}
}运行结果如下: